Закон Ома для последовательно соединенных RLC цепей
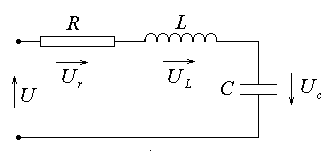
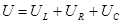 ,
,
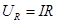 ,
, 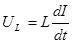 ,
, 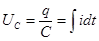 .
.
Дано:
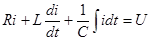 .
.
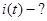 , то есть требуется найти закон изменения тока. Это неоднородное дифференциальное уравнение. Если в правой части стоит 0, то однородное дифференциальное уравнение описывает замкнутую накоротко цепь. При этом энергия на конденсаторе и катушке быстро расходится через сопротивление
, то есть требуется найти закон изменения тока. Это неоднородное дифференциальное уравнение. Если в правой части стоит 0, то однородное дифференциальное уравнение описывает замкнутую накоротко цепь. При этом энергия на конденсаторе и катушке быстро расходится через сопротивление 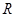 .
.
Полное решение этого уравнения складывается из частного решения неоднородного уравнения и общего решения однородного. Будем искать частное решение неоднородного уравнения в виде 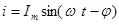 (1), где
(1), где 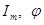 подлежат определению.
подлежат определению.
Продифференцируем уравнение (1) по 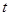 и запишем в виде:
и запишем в виде:
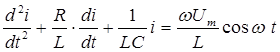 . (2)
. (2)
Найдём 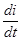 и
и 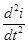 :
:
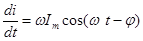 ;
; 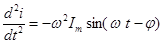 .
.
Подставим эти уравнения в (1):
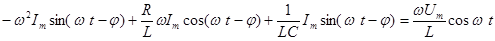 .
.
Имеем синус и косинус разности:
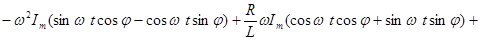
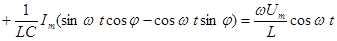 .
.
Для любого момента времени сумма коэффициентов 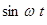 и
и 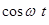 , тогда имеем систему:
, тогда имеем систему:
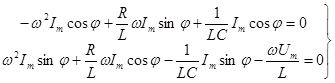
где в первом уравнении - коэффициенты при 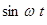 , во втором -
, во втором - 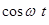 . Решая данную систему, получаем:
. Решая данную систему, получаем:
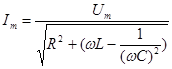 (1),
(1), 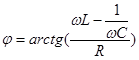 (2).
(2).
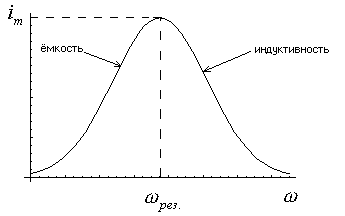
Анализируя данное решение видно, что ток зависит от частоты.
Зависимость тока от частоты.
1) 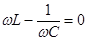 .
.
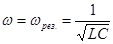 - частота, при которой наступает резонанс (в данном случае ток максимален).
- частота, при которой наступает резонанс (в данном случае ток максимален).
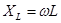 ,
, 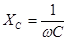 .
.
Пусть 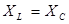 . Тогда из (1) получаем
. Тогда из (1) получаем 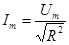 - в этом случае знаменатель минимален и ток максимален.
- в этом случае знаменатель минимален и ток максимален.
Рассмотрим два крайних случая.
2) 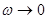 (малые частоты)
(малые частоты) 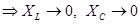 т. е. с уменьшением частоты цепь начинает носить более ёмкостной характер (цепь ведёт себя как ёмкость).
т. е. с уменьшением частоты цепь начинает носить более ёмкостной характер (цепь ведёт себя как ёмкость). 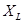 ‡
‡ 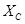 .
.
3) 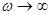
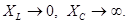 То есть,
То есть, 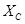 ‡
‡ 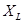 (цепь ведёт себя как индуктивность).
(цепь ведёт себя как индуктивность).
Угол сдвига фаз.
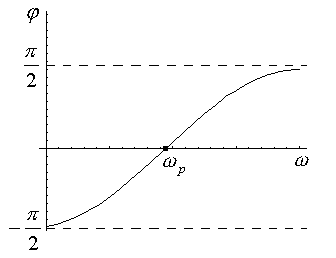
1) 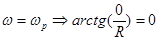 .
.
2) 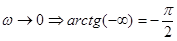 .
.
3) 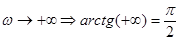 .
.
Построим векторную диаграмму:
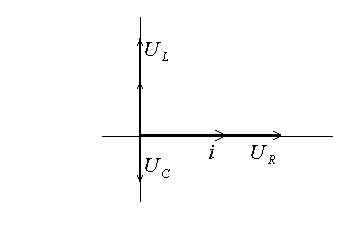 При построении мы использовали соотношение
При построении мы использовали соотношение 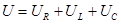 . Ток отстаёт от напряжения на индуктивности на
. Ток отстаёт от напряжения на индуктивности на 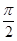 за счёт электромагнитной индукции. На конденсаторе напряжение отстаёт от тока на
за счёт электромагнитной индукции. На конденсаторе напряжение отстаёт от тока на 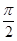 .
.
Резонанс напряжений.
В случае резонанса 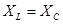 . Ток одинаков, следовательно
. Ток одинаков, следовательно 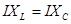 , то есть
, то есть 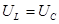 . При этом угол
. При этом угол  равен 0. Векторная диаграмма для этого случая изображена слева.
равен 0. Векторная диаграмма для этого случая изображена слева.
На резонансе цепь ведёт себя, как на активном сопротивлении. Ток имеет максимальное значение:
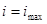 ,
,
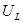 и
и 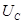 меняются в противофазе.
меняются в противофазе.
Напряжения на емкости и индуктивности на резонансной частоте не достигают своих максимальных значений.
Найдем частоты, при которых напряжения на емкости и индуктивности достигают своих максимальных значений.
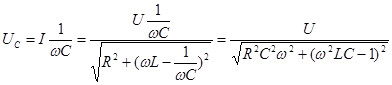 .
.
Напряжение будет максимально, когда будет минимально выражение под корнем. Следовательно:
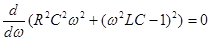 ,
,
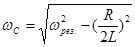 , то есть
, то есть 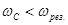 .
.
Следовательно, напряжение на конденсаторе достигает максимума при частоте, меньшей частоты резонанса.
Аналогично для катушки:
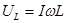 ,
, 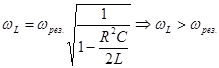 .
.
Следовательно, напряжение на индуктивности достигает максимума при частоте, большей частоты резонанса.
