Регрессионный анализ данных в Mathcad

Тема № 1

Составление математических моделей

Экспериментально-статистическими методами

Лабораторная работа № 1

Определение коэффициентов регрессии методом наименьших квадратов

Цель работы

Нахождение коэффициентов в уравнении регрессии с применением метода наименьших квадратов (МНК) с использованием программы Mathcad.

Теоретические сведения

Метод наименьших квадратов (МНК)

Задача определения параметров уравнения регрессии 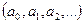сводится к определению минимума функции многих переменных.

Если 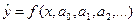есть функция дифференцируемая, то требуется выбрать 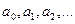при выполнении минимума квадратичного критерия:

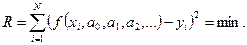(1.1)

Линейное приближение по МНК

Пусть искомая функция f(x, 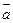) является линейной относительно х. В этом случае задача сводится к отысканию двух параметров а₀ и а₁ в зависимости

f(x, 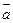)= а₀ + а₁х. (1.2)

Критерий (1.1) примет вид

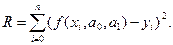(1.3)

Условия минимума этого критерия таковы:

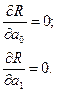(1.4)

Система уравнений (1.4), получаемых дифференцированием выражения (1.3), имеет вид:

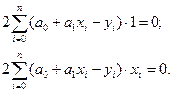(1.5)

или, после преобразований,

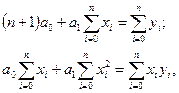(1.6)

Метод Крамера для решения системы линейных уравнений (1.6) приводит к следующим формулам для искомых параметров:

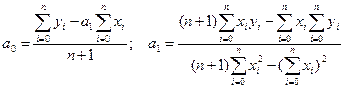(1.7)

Частными случаями уравнения линейной регрессии с одной независимой переменной х являются:

- полиномиальная регрессия, когда

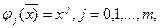(1.8)

и ее разновидности – линейная регрессия от одной переменной (m=1):

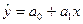(1.9)

и параболическая регрессия (m=2):

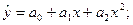(1.10)

- трансцендентная регрессия и ее разновидности

в виде зависимости показательного типа:

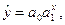(1.11)

которая линеаризуется путем логарифмирования:

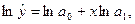(1.12)

и дробно-показательного типа:

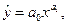(1.13)

которая также линеаризуется путем логарифмирования:

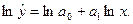(1.14)

Обозначим 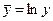, , 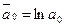, 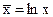тогда после подстановки получим:

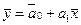. После определения коэффициентов 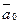, 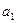и используя операцию, обратную логарифмированию, получим исходное степенное уравнение.

Для обратно-пропорциональной зависимости: если точечный график дает ветвь гиперболы, приближающую функцию можно искать в виде

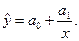(1.15)

Для перехода к линейной функции сделаем подстановку u=1/x.

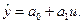(1.16)

Практически перед нахождением приближающей функции вида (1.16) значения аргумента следует заменить обратными числами. Полученные значения парамет­ров а и b подставить в формулу (1.15).

Эмпирическое корреляционное отношение, характеризующее тесноту связи между X и Y, определяется следующим образом:

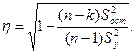(1.17)

Для оценки силы линейной связи вычисляется выборочный коэффициент корреляции:

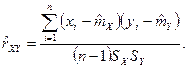(1.18)

Здесь 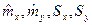определяются по формулам

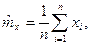
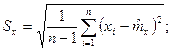(1.19)

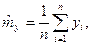
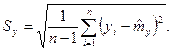(1.20)

Коэффициент корреляции характеризует не любую зависимость, а только линейную. Линейная вероятностная зависимость случайных величин заключается в том, что при возрастании одной случайной величины другая имеет тенденцию возрастать (или убывать) по линейному закону. Если случайные величины Х и У связаны точной линейной функциональной зависимостью у=а₀+а₁х, то 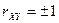; причем знак соответствует знаку коэффициента а₁. В общем случае, когда величины Х и У связаны произвольной стохастической зависимостью, коэффициент корреляции может иметь значение в пределах -1 .

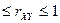Задание

Определить коэффициенты в уравнении регрессии, используя МНК. Исходные данные приведены в табл. 1.1. Работа выполняется по вариантам.

Для построения поля корреляции и проведения регрессионного анализа использовать статистический материал (табл. 1.1).

При определении типа зависимости рассматриваются следующие уравнения регрессии:

· линейное;

· полиномиальное;

· гиперболическое;

· степенное.

Среди данных уравнений выбирается то, которое наиболее точно описывает эмпирическую линию регрессии, построенную на плоскости поля корреляции. Для сравнения качества приближений вычисляем суммы квадратов отклонений.

Коэффициенты выбранного уравнения регрессии 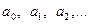определяются в результате решения системы нормальных уравнений.

Таблица 1.1

№ вар.
	x	-1	-0,55	-0,1	-0,35	0,8	1,25	1,7	2,15	2,6	3,05
y	-6,78	-6,56	-6,14	-5,31	-3,68	-0,85	5,81	18,15	42,4	90,03
	x	0,01	0,56	1,11	1,66	2,21	2,28	3,3	3,85	4,4	4,95
y	34,23	5,97	1,28	-1,54	-3,54	-5,09	-6,36	-7,44	-8,37	-9,2
	x	-2	-1,6	-1,2	-0,8	-0,4		0,4	0,8	1,2	1,6
y		10,24	5,76	2,56	0,53		0,64	2,56	5,76	10,24
	x	0,3	1,57	2,84	4,11	5,38	6,65	7,92	9,19	10,46	11,73
y	15,33	4,55	3,41	2,97	2,74	2,6	2,59	2,44	2,38	2,34
	x	-3,5	-2,65	-1,8	-0,95	-0,1	0,75	1,6	2,45	3,3	4,15
y	0,01	0,03	0,07	0,12	0,19	0,2	0,29	0,31	0,325	0,33
	x	0,15	0,94	1,72	2,51	3,29	4,08	4,86	5,65	6,43	7,22
y	-9,69	-4,2	-2,37	-1,25	-0,43	0,21	0,74	1,3	1,58	1,93
	x	0,35	0,82	1,28	1,75	2,21	2,675	3,14	3,605	4,07	4,535
y	6,86	5,23	4,78	4,57	4,45	4,37	4,35	4,28	4,25	4,22
	x	-1	-0,8	-0,6	-0,4	-0,2	0,0	0,2	0,4	0,6	0,8
y	4,14	4,2	4,3	4,45	4,67		5,49	6,85	7,32	8,95
	x		2,3	2,6	2,9	3,2	3,5	3,8	4,1	4,4	4,7
y	2,67	4,06	6,16	8,13	10,92	14,29	18,29	22,97	28,39	34,6
	x	-5	-4	-3	-2	-1
y	0,01	0,02	0,05	0,11	0,21	0,38	0,42	0,47	0,49	0,5
	x	0,95	1,21	1,47	1,74	2,0	2,26	2,52	2,78	3,05	3,31
y	8,16	3,39	2,19	1,34	0,88	0,61	0,54	0,33	0,28	0,19
	x	0,35	0,82	1,28	1,75	2,21	2,68	3,14	3,61	4,07	4,535
y	16,99	8,83	6,61	5,56	4,96	4,62	4,29	4,09	3,93	3,8
	x	-1,7	-1,43	-1,16	-0,89	-0,62	-0,35	-0,08	0,19	0,46	0,73
y	26,96	14,46	7,17	2,92	0,45	-0,98	-1,35	-2,31	-2,6	-2,77
	x	-5	-3,5	-2	-0,5		2,5		5,5		8,5
y		0,01	0,06	0,28	0,87	2,05	2,92	3,23	3,31	3,33
	x	-2	-1,4	-0,8	-0,2	0,4	1,0	1,6	2,2	2,8	3,4
y	6,8	3,33	1,09	0,02	0,27	1,7	4,35	8,23	13,33	19,65

Порядок выполнения работы

1. Ввод исходных данных, построение поля корреляции.

2. Выбор вида уравнения регрессии.

3. Преобразование данных к линейному типу зависимости.

4. Получение параметров уравнения регрессии.

5. Обратное преобразование данных и определение суммы квадратов отклонений найденных значений функции от заданных.

6. Вывод результатов.

Пример

Для построения поля корреляции и регрессионного анализа приведены исходные данные в виде следующей таблицы.

X	Y1
500.0	2000.0
750.0	3000.2
1000.0	5200.0
1250.0	5200.4
1500.0	5679.9
1750.0	6700.0
2000.0	6700.0
2250.0	7559.4
2500.0	7759.4
2750.0	9940.4
3000.0	10900.2
3250.0	11950.1
3500.0	14200.1
3750.0	15100.0
4000.0	16000.0

Задаем исходные данные в следующем виде (в программе Mathcad):

Обозначения: X – входной параметр; Y1 – выходной параметр.

Разделим все множество X на 5 интервалов и на каждом интервале найдем среднее значение Y:

,

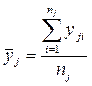где 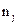– число точек в интервале .

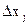Полученные значения запишем в виде:

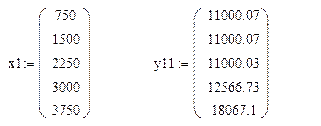
y11 – средние значения для зависимости.

1. Проведем анализ зависимости у11.

1.1. По исходным данным получим поле корреляции Y1=f(X) и по средним точкам построим ломаную (рис. 1.1).

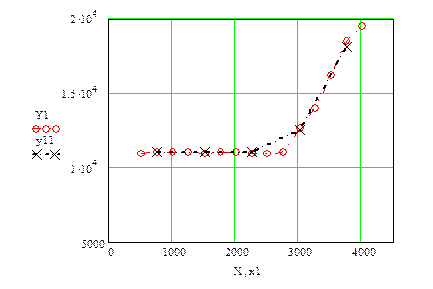
Рис. 1.1. Экспериментальные точки и эмпирическая линия регрессии

1.2. Определим вид уравнения регрессии и параметры уравнения регрессии.

Определим коэффициенты для линейной зависимости:

1 способ: с помощью функции line(x,y)

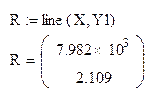
2 способ: по формуле (1.7)

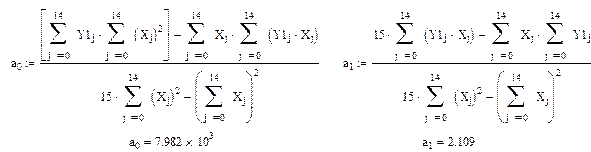
Как видим, коэффициенты совпадают.

Следовательно, линейная зависимость имеет следующий вид:

Y=7,982*10³+2,109X.

Определим коэффициенты для полиномиальной зависимости.

1 способ: по формуле (1.24)

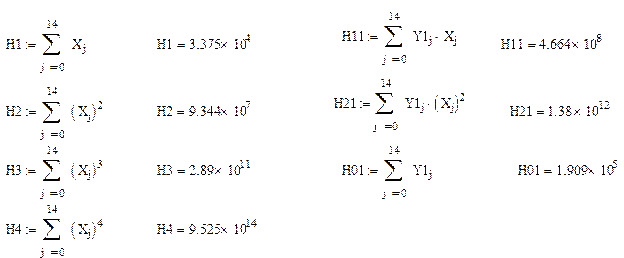
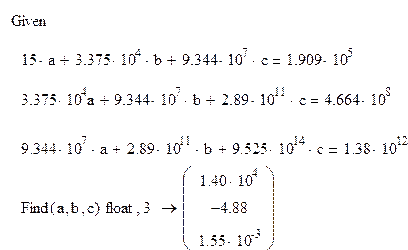
2 способ: с помощью встроенной функции regress(x,y,n), где n – порядок полинома. Примем n=2.

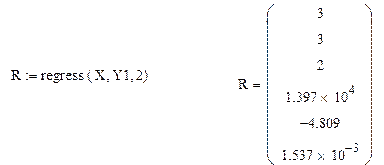
Найденные коэффициенты совпадают.

Параболическая зависимость имеет следующий вид:

Y=1,537*10^-3*X²-4,8X+1,397*10⁴.

Определим коэффициенты для гиперболической зависимости.

1 способ: по формулам (1.16) и (1.24)

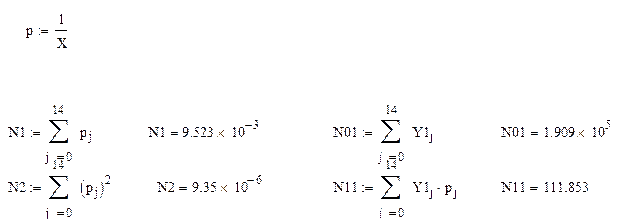
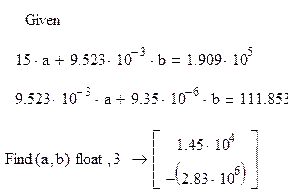
2 способ: по формуле (1.16) и функции line(x,y)

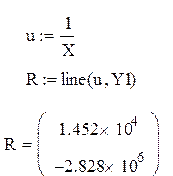
Гиперболическая зависимость имеет следующий вид:

Y=1,452*10⁴-2,828*10⁶/X.

Определим коэффициенты для степенной зависимости.

Применяем формулы (1.14) и (1.24).

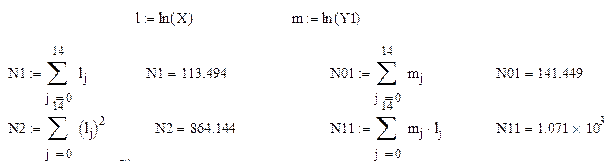
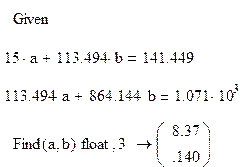a₀= 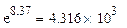; a₁=0,14.

Степенная зависимость имеет вид:

Y=4,316*10³*X^0,14.

1.3. Определим суммы квадратов отклонений вычисленных значений каждой функции от заданных Y1.

Линейная зависимость

Y1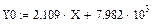

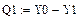
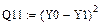
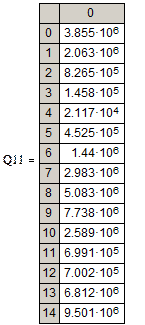
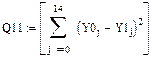
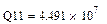
Параболическая зависимость

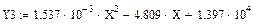
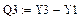
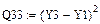
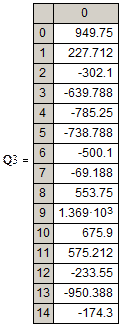
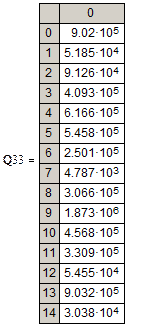
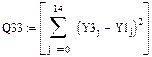
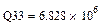
Гиперболическая зависимость

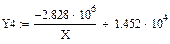
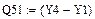
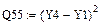
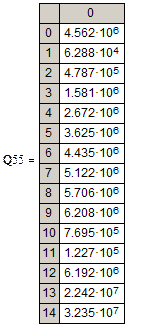
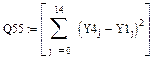
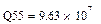
Степенная зависимость

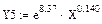
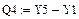
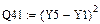
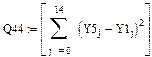
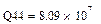
Сравним полученные результаты.

Сумма квадратов отклонений для линейной функции ε= 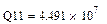, для параболической ε= 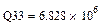, для гиперболической ε= 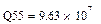, для степенной ε= 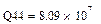. Сравнивая качество приближений, находим, что приближение в виде параболической зависимости в данном случае предпочтительнее.

Лабораторная работа № 2

Регрессионный анализ данных в Mathcad

Цель работы

Проведение регрессионного анализа в Mathcad.

Теоретические сведения

Полиномиальное приближение функций

В тех случаях, когда линейное приближение оказывается неудовлетворительным, т.е. дает значительное отклонение расчетной зависимости от аппроксимируемой, используется приближение полиномами второй степени и выше (m>2) вида:

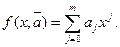(1.21)

Рассмотрим вывод матричной формулы для определения коэффициентов многочлена второй степени (m=2).

Определение параметров а₀, а₁, а₂ по методу наименьших квадратов сводится к нахождению минимума критерия (1.3) как функции трех переменных:

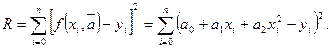(1.22)

Необходимые условия минимума этого критерия имеют вид:

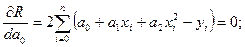
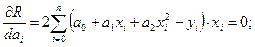(1.23)

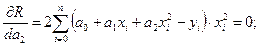
или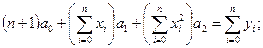

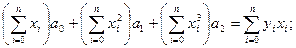(1.24)

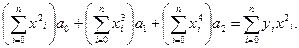
Регрессионный анализ проводится после того, как определен вид уравнения регрессии и найдены значения его коэффициентов. Этот анализ состоит в следующем: проверяется значимость всех коэффициентов уравнения регрессии и устанавливается адекватность уравнения.

При отсутствии параллельных опытов и дисперсии воспроизводимости 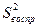остаточная дисперсия определяется следующим образом:

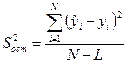. (1.25)

Тогда адекватность принятого уравнения оценивается сравнением 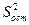и дисперсии относительно среднего :

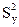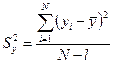(1.26)

по критерию Фишера

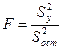. (1.27)

В этом случае критерий Фишера показывает, во сколько раз уменьшается рассеяние относительно полученного уравнения регрессии по сравнению с рассеянием относительно среднего. Чем больше значение F превышает табличное:

, ,

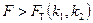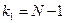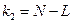
для выбранного уровня значимости р и чисел степеней свободы, тем эффективнее уравнение регрессии.

В MathCAD табличное значение критерия Фишера с учетом принятой доверительной вероятности γ и чисел степеней свободы определяется оператором qF(γ, k1, k2).

Этапы построения уравнений приведены на рис. 1.2.

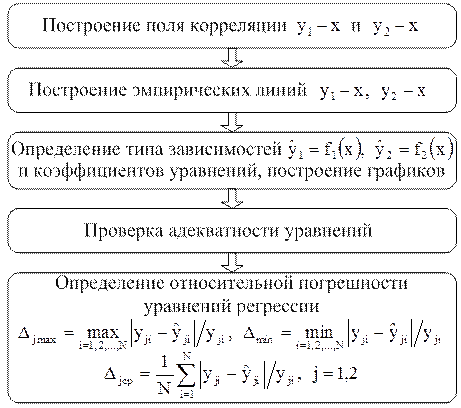
Рис. 1.2. Этапы построения уравнений

Задание

Провести регрессионный анализ для зависимостей, полученных в лабораторной работе № 1. Работа выполняется по вариантам из табл. 1.1 и приложения 2. Этапы построения уравнений приведены на рис. 1.2.

Порядок выполнения работы

1. Проверка адекватности

Проверка адекватности уравнений осуществляется путем расчета остаточной дисперсию 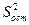и дисперсии относительно среднего 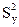. Если критерий Фишера (1.27) будет превышать табличное (приложение 1, 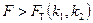, , 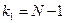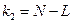), то полученное уравнение адекватно.

2. Затем определяется относительная погрешность уравнений регрессии.

Пример

1. Проверка адекватности выбранного уравнения

Выбираем в качестве приближения параболическую зависимость.

Найдем по формуле (1.17) корреляционное отношение:

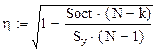
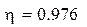
Полученное значение позволяет сделать вывод о высокой тесноте связи между параметрами.

По формулам (1.25)-(1.27) оцениваем адекватность принятого уравнения.

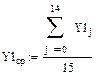
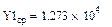
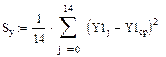
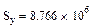
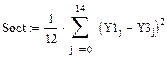
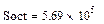
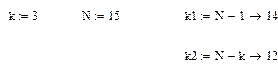
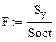
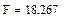
Определяем табличное значение критерия Фишера: 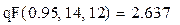или находим по таблице в приложении 1.

18,267>2,637, т. е. 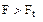, следовательно, модель адекватна.

2. Построение эмпирической линии и графика по уравнению .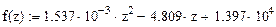

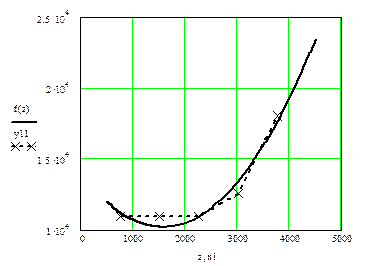
3. Найдем относительную погрешность уравнения регрессии.

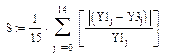
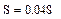
Относительная погрешность=0,048.

Расчет относительной погрешности для зависимости

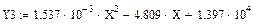
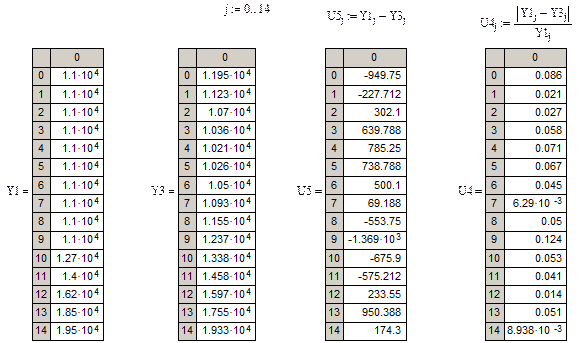
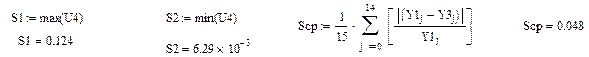
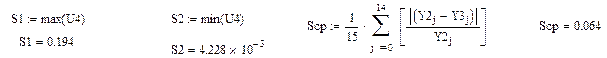
Таким образом, в работе получена математическая модель по результатам пассивного эксперимента. Уравнение адекватно, так как критерий Фишера превышает табличное значение.

Лабораторная работа № 3