Теорема об интегрировании оригинала.

Если 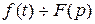, то .

Примеры. Найти оригинал и изображение:

1) ; 2) ; 3) ;

Решение.

1) - по теореме об изображении интеграла.

, тогда .
2) , отсюда .
3) ; , т.о. .
	Вопросы для самопроверки 1.Сформулируйте теорему об интегрирования оригинала

Примеры для самостоятельного решения.

Найти изображения следующих интегралов

1) ;	2) ;	3) ;
4) ;	5) ;	6)

Ответы:

1) ;	2) ;	3)
4) ;	5) ;	6)

Изображение периодического оригинала.

Теорема.Если 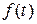-периодический оригинал с периодом , то его изображение определяется по формуле .

На практике же для нахождения изображения периодического оригинала 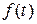вводят функцию , которую представляют в виде . Изображение этой функции обозначают и находят с помощью рассмотренных ранее методов, а изображение функции 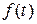можно выразить по формуле .

Примеры

1)Найти изображение последовательности единичных прямоугольных импульсов длительности повторяющихся с периодом .

Решение. Изобразим последовательность импульсов:

Запишем оригинал и найдем изображение

, ,

2) Найти изображение “пилообразной” функции:

Решение. Запишем оригинал и найдем его изображение:

3) Найти изображение следующей периодической функции:

Решение.

, .

Вопросы для самопроверки

1. Сформулируйте теорему об изображении периодического оригинала

Примеры для самостоятельного решения.

Найти изображения следующих периодических функций:

1)

2)

3)	4)
5)	6)

Ответы.1) ; 2) ;

3) ; 4) ;

5) ;

.

Свертка. Изображение свертки.

Определение.Сверткой двух функций-оригиналов называется интеграл .

Свертки обладают следующими свойствами:

1.

2.

3.

Теорема об изображении свертки.

Если и , то .

Примеры 1-6. Восстановить оригинал, используя определение свертки.

1)

Решение.

;

2)

Решение.

;

В следующих примерах для восстановления оригиналов будем использовать таблицу сверток, приведенную в конце пособия.

3)

Решение.

.

По таблице сверток находим, что

4)

Решение.

По таблице сверток находим, что это соответствует оригиналу .

5)

Решение.

По таблице сверток находим, что эта свертка соответствует оригиналу

6) .

Решение.

, а это соответствует оригиналу

Вопросы для самопроверки

1. Дайте определение свертки

2. Сформулируйте теорему об изображении свертки

Примеры для самостоятельного решения.

Восстановить оригиналы, используя свертку.

1) ;	3) ;
2) ;	4)

Ответы.

1) ;	3) ;
2) ;	4) ;

Восстановление оригиналов по изображению.

Заключительный шаг схемы применения операционного исчисления состоит в нахождении оригинала по полученному изображению, этот шаг или эту операцию называют обратным преобразованием Лапласа и символически записывают следующим образом: .

Раcсмотрим основные способы восстановления оригиналов по изображениям.