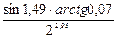Применение полного дифференциала в приближенных вычислениях
Частные производные и дифференциалы функций нескольких переменных
Справочный материал
Частные производные 1 порядка функции нескольких переменных
Определение. Пусть функция z=f(x;y) определена в некоторой окрестности точки М(x;y).
Частной производной функциив точке (x;y) по переменной x (по переменной y) называется конечный предел отношения частного приращения функции по переменной x (по переменной y) к приращению аргумента Dx (Dy) при стремлении последнего к нулю
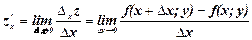 (1)
(1)
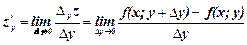 . (1/)
. (1/)
Запись: z¢x, f ¢x, 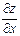 ,
, 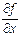
z¢у, f ¢у, 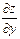 ,
, 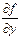 .
.
Замечание:
1.Частная производная функции двух переменных равна обычной производной функции одной переменной, полученной при условии, что вторая независимая переменная сохраняет постоянное значение.
2.Частные производные функции нескольких переменных по каждому из ее аргументов определяются при условии, что все остальные аргументы постоянные.
Дифференциалы функции нескольких переменных
Частные дифференциалы функции z=f(x;y)
dx z = z¢x dx = 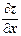 dx - частный дифференциал функции z=f(x;y) по переменной x (2)
dx - частный дифференциал функции z=f(x;y) по переменной x (2)
dу z = z¢у dу = 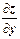 dу- частный дифференциал функции z=f(x;y) по переменной y (2/)
dу- частный дифференциал функции z=f(x;y) по переменной y (2/)
Полный дифференциал функции z=f(x;y)
dz = dx z + dу z или
dz = 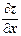 dx +
dx + 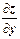 dy (3)
dy (3)
Замечание:
1. Полный дифференциал функции нескольких переменных u=f(x; y; . . . ;t), если он существует, равен сумме всех ее частных дифференциалов
du = 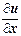 dx +
dx + 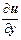 dy + … +
dy + … + 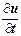 dt(3/)
dt(3/)
2. Для дифференциалов функции двух переменных сохраняются правила их вычисления, известные для дифференциалов функции одной переменной
 d(u ± v) = du ± dv
d(u ± v) = du ± dv
d(u×v) = vdu + udv
d( 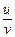 )=
)= 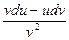 .
. 
Применение полного дифференциала в приближенных вычислениях
Если Dz=f(x0 +Dx; y0 +Dy) – f(x;y) полное приращение функции z=f(x;y), то при достаточно малых Dx и Dy справедлива формула
Dz » dz (4)
Ввиду того, что вычисление полного дифференциала функции значительно проще вычисления ее полного приращения, то формулу (4) используют в приближенных вычислениях в виде:
f(xo +Dx; y0 +Dy) 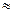 f(x0; y0) + fx/(x0;y0)×Dx + fу/(x0;y0)×Dу (5)
f(x0; y0) + fx/(x0;y0)×Dx + fу/(x0;y0)×Dу (5)
где Dx=dx, Dу=dy – дифференциалы независимых переменных совпадают с их приращениями
Задачи
1. Найти частные производные указанных функций.
1) z = x2 + 2y2 – 3xy – 4x + 2y + ln 5 2) z = (x3 +y3 – xy2)3 3) z = ln (x2 +2y3)
4) z = (1 + x2)y 5) z = arcsin 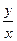 6) u =
6) u = 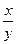 +
+ 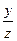 -
- 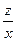
7) u = arctg 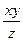 8) u = ln
8) u = ln 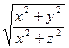 9) u = (x×y) Z
9) u = (x×y) Z 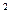
10) z = x 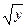 +
+ 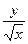 11) z = ln (x +
11) z = ln (x + 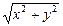 ) 12) z = (x -
) 12) z = (x - 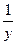 )e-x
)e-x 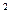 y
y
13) z = arcsin 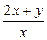 14) u = sin2(3x + 2y - z).
14) u = sin2(3x + 2y - z).
2. Вычислить значения частных производных функции в указанной точке
1) z = x + y + 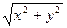 M0 (3; 4)
M0 (3; 4)
2) z = cos (3x – 5y) M0 ( 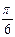 ; 0)
; 0)
3) z = ln (x2 – y2) M0 (2; -1)
4) u = ln (1 + x + y2 + z3) M0 (1;1; 1).
3. Проверить, что функция удовлетворяет уравнению
а) z = xln 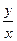 x
x 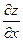 + y
+ y 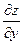 = z
= z
б) z = xy 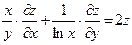
в) u = x + 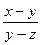
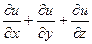 = 1.
= 1.
4. Найти частные и полные дифференциалы функций
а) z = 3x2y5
б) u = 2xyz
в) z = arccos 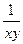
г) z = x3 + xy2 + x2y
д) u = sin2(xy2z3)
e) z = 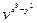
ж) z = yln2x
з) u = 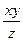
и) z = sin2y cos2x
5. Вычислить значение полного дифференциала функции:
а) z = arcctg 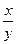 при x = 1; y = 3; dx = 0,01; dy = - 0,05
при x = 1; y = 3; dx = 0,01; dy = - 0,05
б) z = 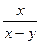 при x = 2; y = 1; dx = -
при x = 2; y = 1; dx = - 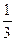 ; dy =
; dy = 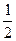
в) u = 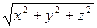 при перемещении точки М (x; y; z) из положения М0 (10; - 10; 5) в М1 (9; - 11; 6).
при перемещении точки М (x; y; z) из положения М0 (10; - 10; 5) в М1 (9; - 11; 6).
6. Вычислить приближенное значение выражения, исходя из значения функции в точке М0, и заменяя ее приращение дифференциалом:
а) 1,942 е0,12 б) sin1,59 tg3,09 в) 2,68sin0,05
z = x2ey, M0 (2; 0) z = sinx tgy, M0 ( 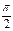 ;
; 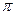 ) z = xsin y , M0 (е; 0).
) z = xsin y , M0 (е; 0).
7. Вычислить приближенное значение выражения:
а) (1,02)3 × (0,97)3 б) 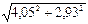 в) 1,083,96 г)
в) 1,083,96 г)