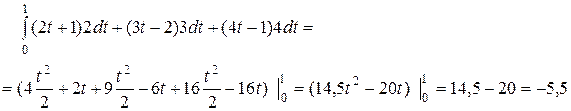Криволинейный интеграл II рода

Рассмотрим пространство R². Пусть в области DÌR² определены две непрерывные функции P(x,y), Q(x,y), тогда в любой точке М(x,y) Î D определена векторная функция `F(x, y) = (P(x, y); Q(x, y)), которую в векторной форме можно записать в виде: .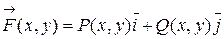

Пусть функции P(x, y) и Q(x, y) определены в точках гладкой дуги 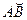кривой L Ì D. Разобьем дугу 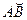на части точками М₁,М₂, ...М_n. На каждой дуге 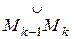возьмем произвольную точку 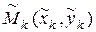и вычислим значение .

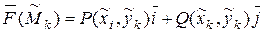Пусть [a, b]и[c, d] – проекции 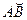на OX и OY соответственно, т.е. xÎ[a,b], y Î [c, d], когда М(х, у) Î 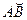. Каждую частичную дугу спроектируем на оси координат, получим разбиение отрезков [a, b]и[c, d] на n частей, длины частичных интервалов обозначим соответственно Dх_k и Dy_k. Составим интегральную сумму вида:

.

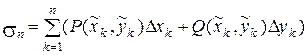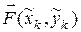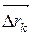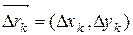Эта сумма представляет собой сумму скалярных произведений векторов на векторы , где , т.е.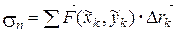

Обозначим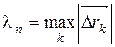

Определение 5.1

Если существует 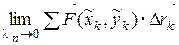, не зависящий ни от способа разбиения дуги 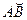на части, ни от выбора точки 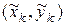, то этот предел называется криволинейным интегралом II рода и обозначается 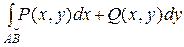или .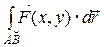

Итак, криволинейный интеграл II рода

,

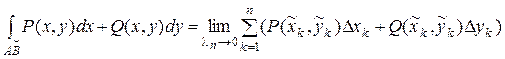Заметим, что условие 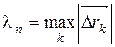→0 равносильно условиям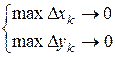

В отличие от криволинейного интеграла I рода, который еще называют интегралом по длине дуги, криволинейный интеграл II рода называют криволинейным интегралом по координатам.

Свойства:

1. 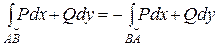- меняет знак при изменении ориентации кривой (направления движения по кривой).

2. Свойство линейности, аддитивности (АВ = АС + СВ) аналогичны свойствам криволинейного интеграла I рода. В частности,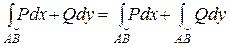

3. Связь между криволинейными интегралами I и II рода выражает формула: ,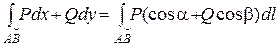

где (cosa,cosb) – направляющие косинусы касательной к дуге АВ в любой ее точке.

Способы вычисления криволинейного интеграла II рода:

1) Если АВ: y = j(x), x Î [a, b], то dy = j¢(x)dx и

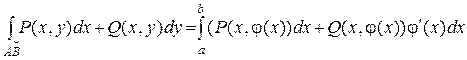
2) Если АВ: x = y(y), y Î [c, d],то dx = y¢(y)dy и

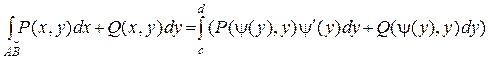
3) Если АВ: 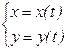, t Î [a,b], dx = x¢(t)dt, dy = y¢(t)dt, то

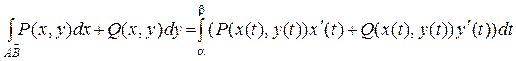
Аналогично можно дать определение криволинейного интеграла II рода по пространственной кривой

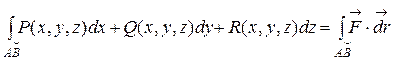
Пример 2.

Вычислить 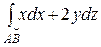, где АВ – отрезок прямой между точками В(1, 1, 1), А(0, 0, 2).

Решение:Найдем уравнение АВ:

.

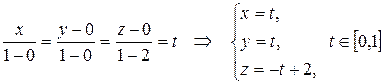Тогда 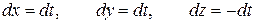, значит,

.

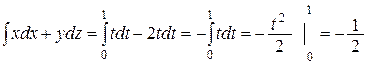Физический смысл криволинейного интеграла II рода:

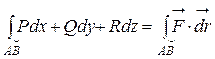
определяет работу силы 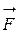при перемещении материальной точки вдоль кривой L из положения А в положение В. Действительно, пусть материальная точка M(x,y) движется вдоль некоторой плоской (можно аналогично рассмотреть и пространственную) кривой L от точки A к точке B. Пусть вдоль кривой действует сила 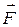, которая меняется по величине и направлению при перемещении точки M, т.е. сила 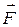является функцией точки: 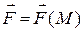. Найдём работу A силы при перемещении точки из положения A в положение B.

Как известно, в случае, когда сила постоянна, а путь прямолинейный, работа равна 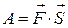(*), т.е. скалярному произведению вектора силы 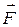на вектор перемещения 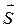. Воспользуемся этим фактом и для решения поставленной задачи.

1) Разобьём дугу AB в направлении от точки A к точке B на n частей точками A=M₀,M₁, M₂,…, M_n=B и обозначим через 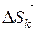вектор 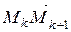. Тогда

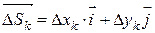
(рис.34). Пусть λ – наибольшая из длин этих векторов, т.е.

.

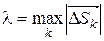2) На каждой элементарной дуге выберем произвольную точку 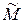_k(x_k,y_k) и предположим, что в пределах каждой элементарной дуги сила 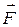постоянна и равна 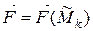. Тогда в силу (*), скалярное произведение 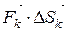можно рассматривать как приближённое значение работы A_k силы вдоль дуги .

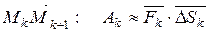Пусть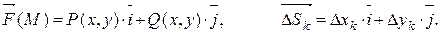

Тогда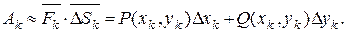

3) Искомая работа A силы на всей дуге AB будет приближённо равна

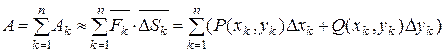
и это приближённое равенство тем точнее, чем меньше λ.

4) Следовательно, истинное значение работы A силы 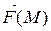при перемещении точки M по дуге AB получим, переходя к пределу при λ→0: = .

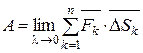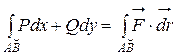Рассмотрим замкнутую кривую C, будем называть ее замкнутымконтуром. Ориентацию на этой кривой выберем следующим образом: если при движении точки М вдоль кривой ограниченная этим контуром область G остается слева, то направление движения (ориентацию на кривой) будем считать положительным. В противном случае – отрицательным.

Криволинейный интеграл II рода по замкнутому контуру будем обозначать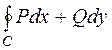

Справедлива

Теорема 5. 1 (формула Грина)

Пусть С – положительно ориентированная замкнутая кривая, ограничивающая область D, а функции P(x, y) и Q(x, y) непрерывны вместе со своими производными 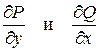в области D и на границе C. Тогда имеет место равенство

.

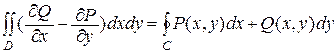(без доказательства). Это равенство называют формулой Грина.

Пример 3.

Вычислить .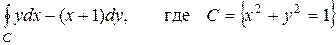

Решение:Здесь Р(х, у) = у, Q(x, y) =(x+1), 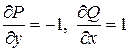. Тогда по формуле Грина

.

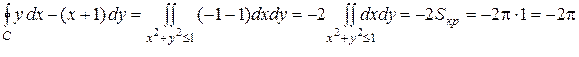Здесь мы используем свойство двойного интеграла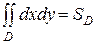

Заметим, что если 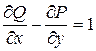, то

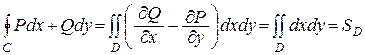
Рассмотрим три случая:

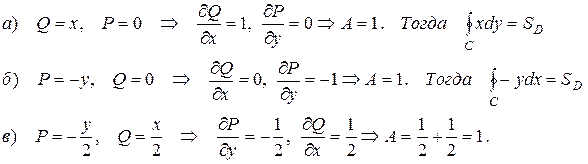
Тогда

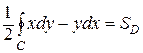
Таким образом, с помощью криволинейного интеграла II рода по замкнутому контуру С можно найти площадь области, ограниченной этим контуром:

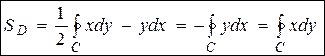
Справедливо также следующая важная

Теорема 5.2

Если функции P(x, y) и Q(x, y) непрерывны вместе со своими производными 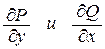в области D и 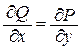, то следующие утверждения эквивалентны:

1. для любого замкнутого контура ;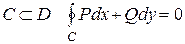

2. 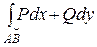- не зависит от пути интегрирования АВ, а зависит только от начальной А и конечной В его точек и обозначается: 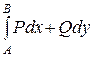. Условие 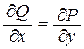при этом называют условием независимости криволинейного интеграла от пути интегрирования.

3. существует функция и(х,у) такая, что 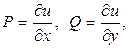а 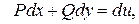и тогда

.

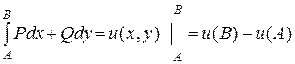Доказательство первого из этих утверждений легко следует из формулы Грина. Доказательство второго из этих утверждений проведите или изучите самостоятельно.

Третье утверждение рассмотрим без доказательства. Отметим только его важный смысл: равенство 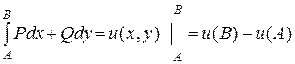, по существу, представляет аналог формулы Ньютона-Лейбница для криволинейного интеграла второго рода. Если при этом А(х₀, y₀) – некоторая фиксированная точка, а В(x, y) – текущая точка области D, то

,

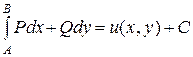что означает аналог теоремы Барроу, где С = - u(х₀, y₀). Таким образом, если по известному дифференциалу 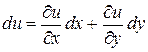функции двух переменных требуется найти функцию u(х, y), нужно вычислить криволинейный интеграл второго рода от выражения du по любому пути, соединяющему произвольную фиксированную точку (х₀, у₀) области определения функций 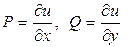и текущую точку (х, у). Очевидно, такие функции определяются с точностью до константы.

Пример 4.

Вычислить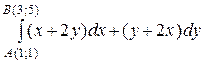

Так как P = x+2y, Q = y+2x – непрерывные функции, 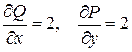– тоже непрерывные и выполняется условие 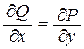, то интеграл не зависит от вида кривой, а зависит только от точек (1, 1) и (3, 5). Значит, можно выбрать любую линию, их соединяющую.

Рассмотрим ломанную АСВ, где С (3, 1), со звеньями, параллельными осям координат. Тогда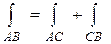

Но АС: y = 1, dy = 0, x Î [1, 3],

CB: x = 3, dx = 0, y Î [1, 5].

Тогда

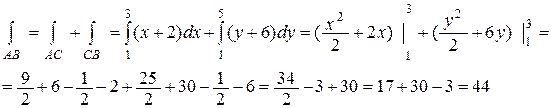
Рассмотрим прямую АВ: 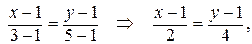2(x-1) = (y-1), откуда

y = 2x-2+1, y = 2x-1, а dy = 2dx. Тогда

.

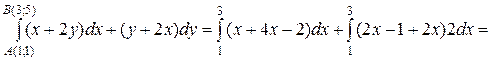
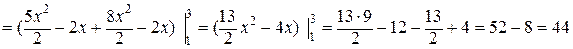Пример 5.

Найти функцию U(x,y) по ее дифференциалу

dU = ( x⁴+ 4xy³)dx + (6x³y² - 5y⁴)dy.

Решение:Убедимся в том, что для P=x⁴+4xy³ и Q=6x³y²-5y⁴ выполняется условие .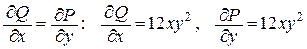

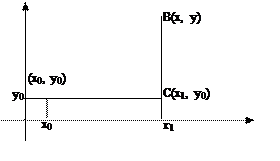Тогда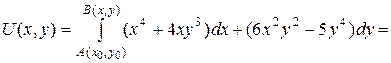

= ,

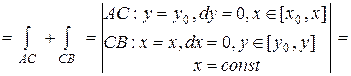
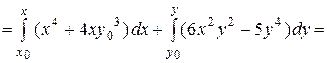
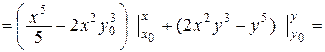
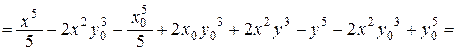
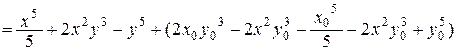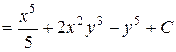где .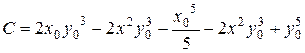

Если взять (х₀, y₀)= (0, 0), получим:

.

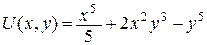В случае функции 3-х переменных и пространственной кривой L, условия независимости интеграла 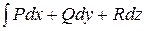от пути интегрирования (или того, что 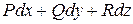есть дифференциал некоторой функции) имеют вид:

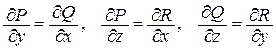
Пример 6.

Вычислить .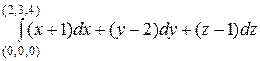

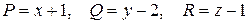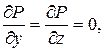
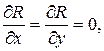
Решение:Здесь , , 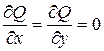значит, данный криволинейный интеграл не зависит от пути интегрирования, в только от начальной (0, 0, 0) и конечной (2, 3, 4) точек. Возьмем, например отрезок прямой, соединяющей эти точки, его уравнения

.

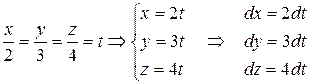Тогда