IV. Интегральный признак Коши

Признаки Даламбера и Коши не всегда являются эффективными при исследовании характера данного ряда.

Рассмотрим еще один признак, который позволяет иногда решать вопрос о сходимости ряда с положительными членами в тех случаях, когда рассмотренные выше признаки оказываются неприодными.

Этот признак основан на сравнении данного ряда с некоторым несобственным интегралом I рода от функции 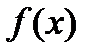, значения которой при последовательных целых значениях аргумента дают все члены этого ряда.

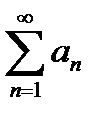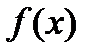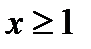Теорема 6.2.10..Дан положительный ряд (6.2.1); если существует не возрастающая непрерывная ф-ия , где , такая, ч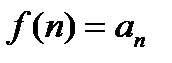то , то

1)ряд (6.2.1) сходится, если сходится несобственный интеграл 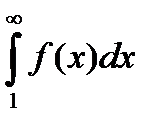; и

2)расходится, если этот интеграл расходится.

Пример 6.2.16.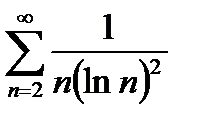

Предположим 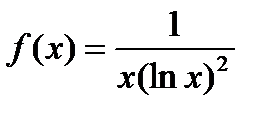- непрерывная, при 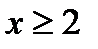функция, убывает с возрастанием х.

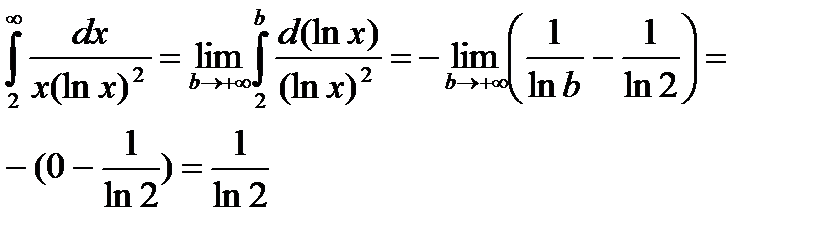
Несобственный интеграл сходится, следовательно, данный ряд сходится.

Пример 6.2.17. Исследовать на сходимость ряд 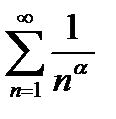, где a - любое действительное число, т. е.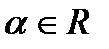

1) непосредственно видно, что при 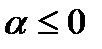член ряда 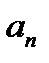стремится к нулю при неограниченном возрастании n, т. е. не выполняется даже необходимый признак сходимости ряда, и , следовательно, ряд расходится.

2)пусть теперь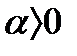

Как легко проверить, признак Даламбера и Коши вопроса о сходимости этого ряда не решают. С помощью же интегрального признака вопрос о сходимости этого ряда решается легко.

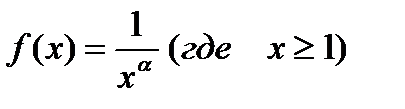- эта функция удовлетворяет всем условиям теоремы, рассмотренной выше.

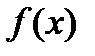( - непрерывна, положительна и убывает при )

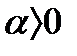Вопрос о сходимости ряда эквивалентен вопросу о сходимости несобственного интеграла

(*).

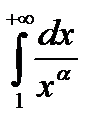При каких 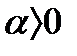существует интеграл (*)?

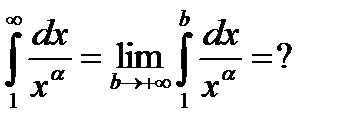
Вычислим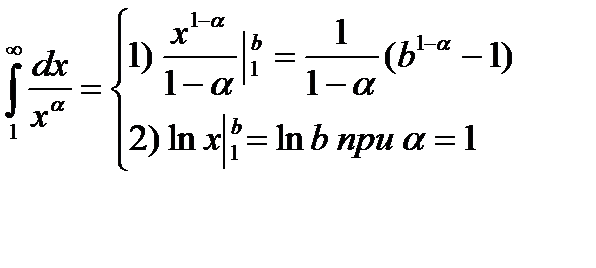

а) пусть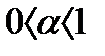

Тогда 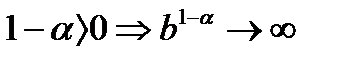при 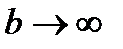и интеграл

Ряд расходится.

б) пусть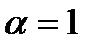

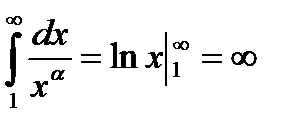- ряд расходится

в) пусть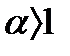

Тогда 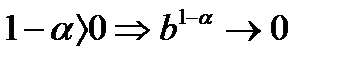при 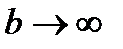Следовательно ряд сходится , т. к.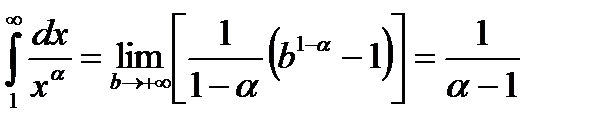

Вывод.Ряды вида 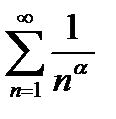1)сходятся при 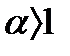и 2) расходятся при 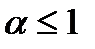, где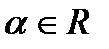

Замечание 6.2.3.При 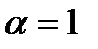ряд обращается в гармонический: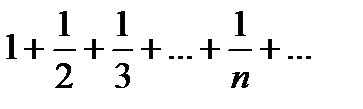

Выше мы рассмотрели теоремы сравнения, основанные на сравнении друг с другом двух рядов.

Какие же ряды используются для сравнения ?

При непосредственном применении теоремы сравнения в основном пользуются рядами:

1)геометрическим рядом 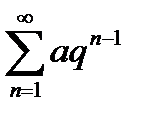(сходящимся при );

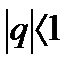2)рядами 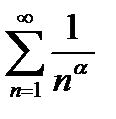(сходящимися при )

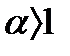Пример 6.2.18.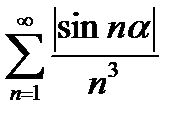

Оценим общий член ряда: 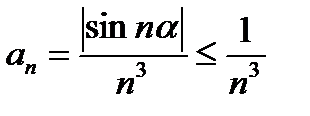, но ряд с общим членом = 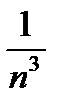сходится (a=3).

Поэтому по теореме 1 признаков сравнения данный ряд также сходится.

Пример 6.2.19.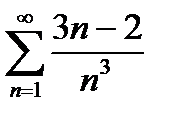

, ,

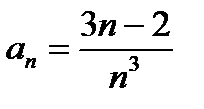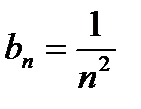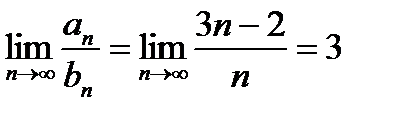
ряды сходятся или расходятся одновременно, т. к. 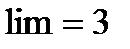. Но ряд с 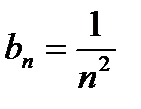- сходится. Поэтому данный ряд также сходится.

ЗНАКОПЕРЕМЕННЫЕ РЯДЫ

Ряды, содержащие бесконечное множество как положительных, так и отрицательных членов.

Прежде всего остановимся на частном случае – на так называемых знакочередующихся рядах.

Знакочередующиеся ряды

Ряды, у которых каждые два соседних члена имеют противоположные знаки.

Обычно знакочередующийся ряд записывают в виде:

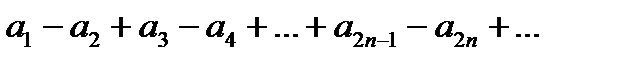
где 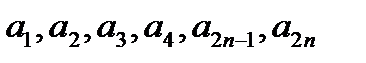- модули членов этого ряда

Теорема Лейбница (признак Лейбница) 6.2.11.

Если члены знакочередующегося ряда удовлетворяют условиям:

1) ;

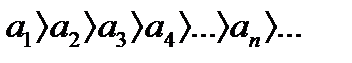2) 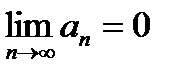, такой ряд сходится.

Пример6.2.20.Найти с точностью до 10^-3 сумму ряда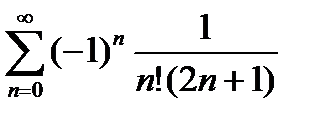

Ряд сходится, т. к. удовлетворяет всем условиям признака Лейбница.

Прежде всего надо знать, сколько слагаемых придется вычислять.

По правилу оценки погрешности вычисления надо взять столько членов, чтобы выполнялось неравенство

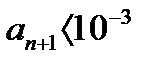
Тогда остаток ряда, начинающийся с этого члена, будет также меньше 10^-3.

Следовательно, решаем неравенство:

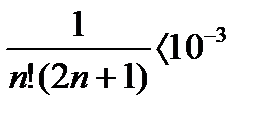
Это неравенство удовлетворяется уже при n=4.

Д-но,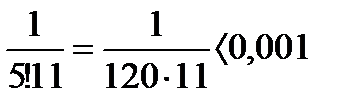

Следовательно, начиная с члена 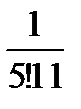, можно отбросить все члены ряда и вычислить только первые пять членов ряда.

Замечание 6.2.4. Практически удобнее находить число слагаемых так: записывают несколько первых членов ряда, а именно:

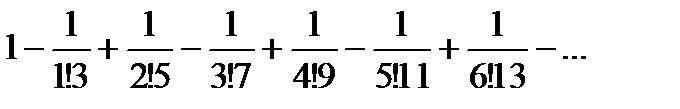
Видно, что модуль 6-го члена (по сету) меньше 10^-3.

Чтобы гарантировать требуемую точность, вычисляют каждое слагаемое с 4-мя знаками после запятой, делая при необходимости округление на 4-ом знаке.

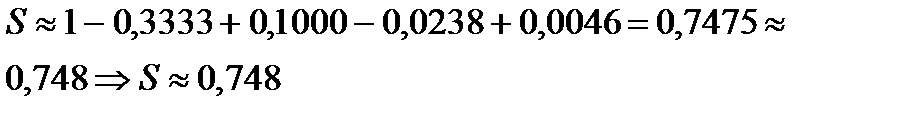
(Все 3 цифры после запятой верные).

Замечание 6.2.5.Признак Лейбница для знакочередующихся рядов является лишь достаточным признаком сходимости, но не необходимым ( т. е. ряд может сходится, хотя по признаку Лейбница не выполняется).