Возникновение скачков уплотнения (СУ) при торможении потока. Изменение параметров потока при прохождении через СУ

При полете ВС со сверхзвуковой скоростью (рис. 2.3) обтекание различных его частей можно представить на примере обтекания ромбовидного профиля крыла (одна из наиболее благоприятных форм профиля крыла сверхзвукового самолета).

Обычный дозвуковой профиль с тупой профилированной передней кромкой можно использовать только для полетов на дозвуковых скоростях.

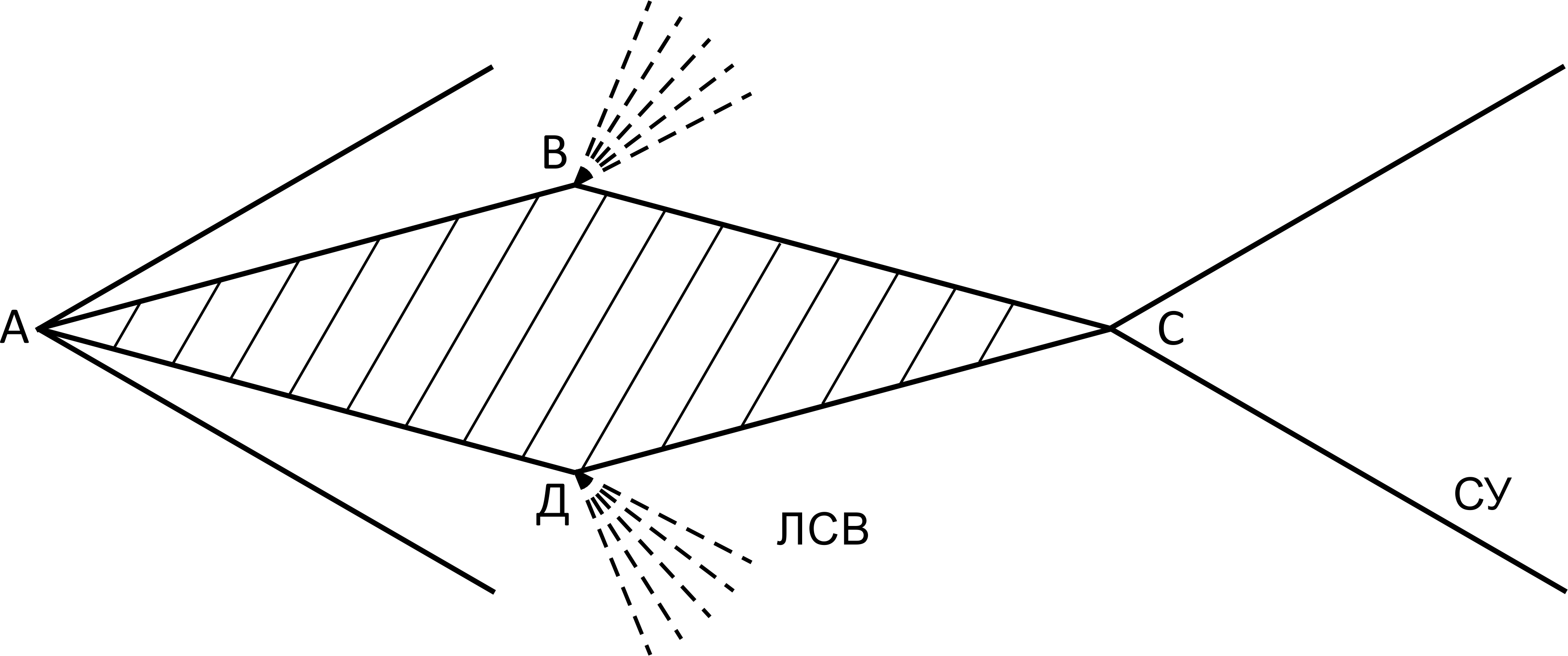
Рис. 2.3 Обтекание ромбовидного профиля крыла ВС сверхзвуковым потоком

Рассматривая рис.2.3, можно отметить, что в окрестности точек В и Д возникают линии слабых возмущений (ЛСВ) или характеристики, а в окрестности точек А и С – скачки уплотнения (СУ).

Такой профиль, а также любой сложный контур самолета можно представить как совокупность внутреннего и внешнего тупых углов.

Вследствие этого, обтекание ромбовидного профиля в окрестности точек В и Д можно представить как обтекание внешнего тупого угла (рис.2.4 а), т.е. тупого угла больше 180°. А обтекание ромбовидного профиля в окрестности точек А и С (рис.2.4 б), можно представить как обтекание внутреннего тупого угла, т.е. тупого угла меньше 180°.

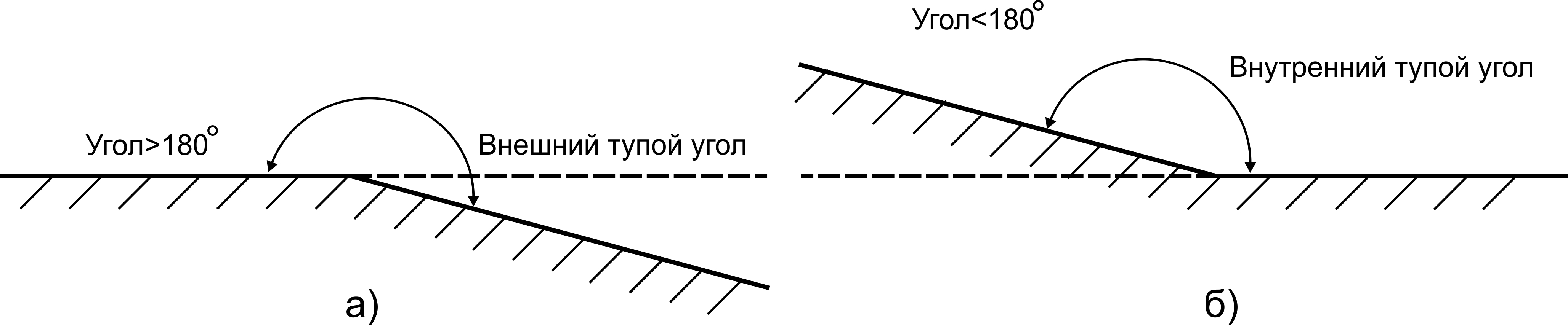
Рис. 2.4 Внешний и внутренний тупые углы для анализа обтекания профиля сверхзвуковым потоком

Рассмотрим вначале первый случай.

Течение Прандтля-Майера или обтекание внешнего тупого угла (φ> 180°)

Обтекание сверхзвуковым потоком внешнего тупого угла в окрестности точки А характеризуется плавным разворотом всех струек на дополнительный угол σ. В точке А плоскопараллельный поток отклоняется и приобретает направление наклонной стенки, т.е. точка А является точкой излома контура поверхности ВС (рис.2.5).

В области поворота потока – угла NВK между линиями слабых возмущений происходит поворот потока на бесконечно малые углы, вследствие чего параметры потока также изменяются на бесконечно малые величины.

Известны параметры сверхзвукового потока перед началом поворота:

- термодинамические параметры: ;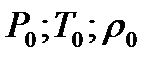

- кинематические параметры: .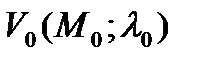

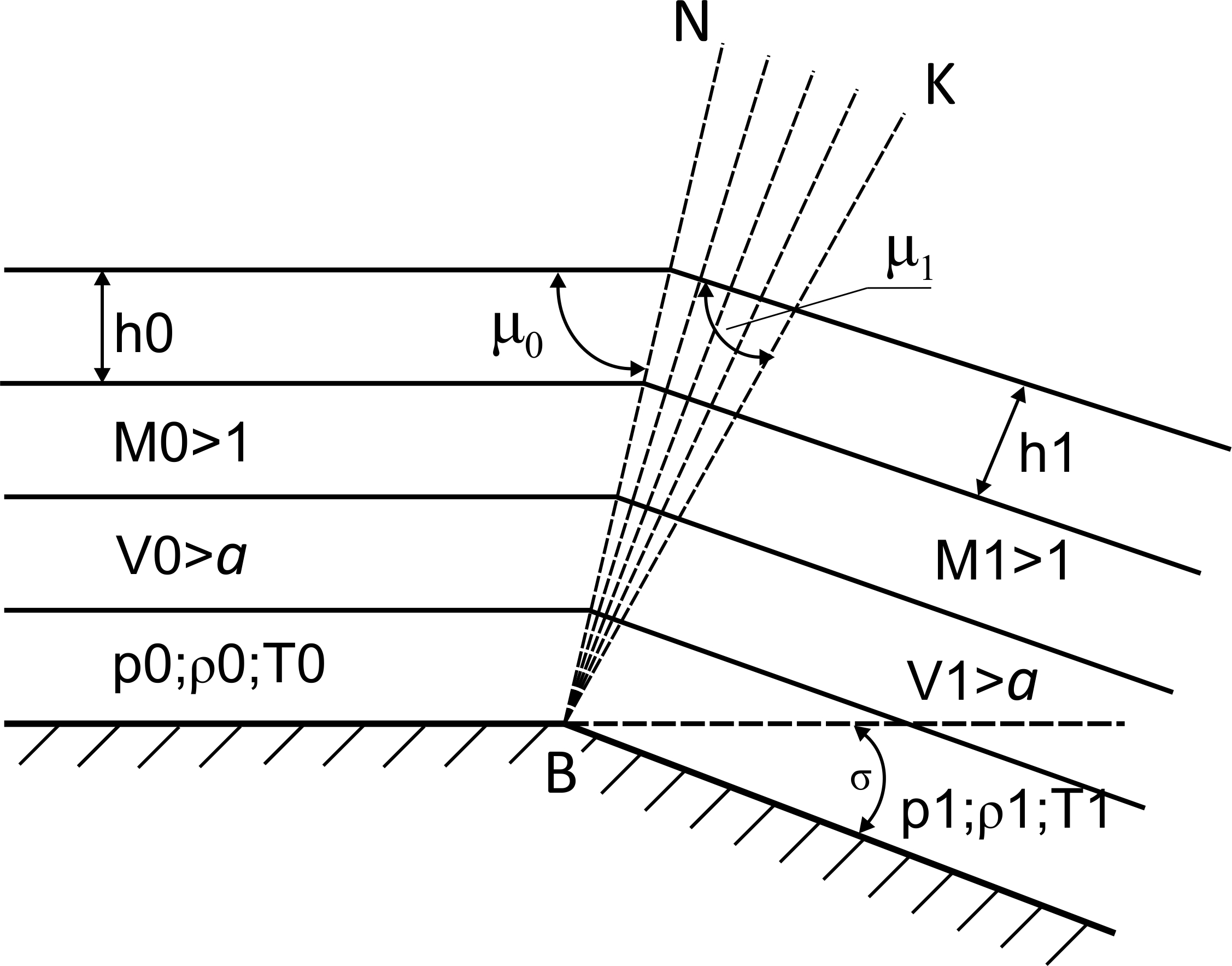
Рис. 2.5 Течение Прандтля-Майера

Анализ уравнения Гюгонио (раздел 1.4)

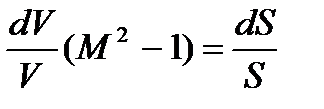
показывает, что при расширении сверхзвукового потока скорость в отдельных струйках увеличивается. Расширение определяется поворотом потока после прохождения точки А: расстояние h между струйками увеличивается.

Для анализа изменения угла Маха используем уравнение (2.1), которое показывает: угол Маха m₁ за областью поворота уменьшается по отношению к соответствующему углу m₀ перед областью поворота (M₁ > M₀ и m₁ < m₀) .

С учетом известного уравнения энергии (раздел 1.3)

,

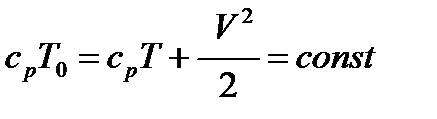можем утверждать, что термодинамические параметры p, r и T при обтекании внешнего тупого угла уменьшаются (скорость и температура в уравнении энергии обратно пропорциональны).

Таким образом, течение Прандтля-Майера – это возникновение слабых возмущений при расширении сверхзвукового потока (вследствие поворота). Поворот происходит не сразу по всему поперечному сечению: на линиях тока, удаленных от стенки, он начинается позднее, чем на расположенных вблизи нее. Это происходит потому, что возмущения распространяются со скоростью звука, но сносятся вниз по потоку со сверхзвуковой скоростью.

Линия NB (начальная ЛСВ) – граница между набегающим потока и областью поворота NBK. Если бы поворот был бесконечно малым, то можно было бы ограничиться одной линией NB, пересекая которую поток повернулся бы на бесконечно малый угол и изменил свои параметры на бесконечно малые величины. При конечном угле поворота σ сверхзвуковой поток поворачивается, пересекая множество линий слабых возмущений в области NBK, подобных линии NB, где BK – конечная линия поворота. Поэтому в совокупности его параметры изменяются на конечные величины.

Возникновение скачков уплотнения (СУ) при торможении сверхзвукового потока

При обтекание сверхзвуковым потоком тела конечных размеров (например, ВС) образуются так называемые сильные возмущения или разрывы: ударные волны (движущиеся) или скачки уплотнения (неподвижные относительно наблюдателя). При переходе через поверхность разрыва термодинамические параметры p, r и T возрастают, а скорость V – уменьшается. Причем, эти изменения происходят резко, скачком: значения параметров в 2-х бесконечно близких точках, разделенных этой поверхностью, отличаются на конечные величины.

Образование скачков уплотнения рассмотрим на примере обтекания внутреннего тупого угла (φ< 180°), который показан на рис. 2.6.

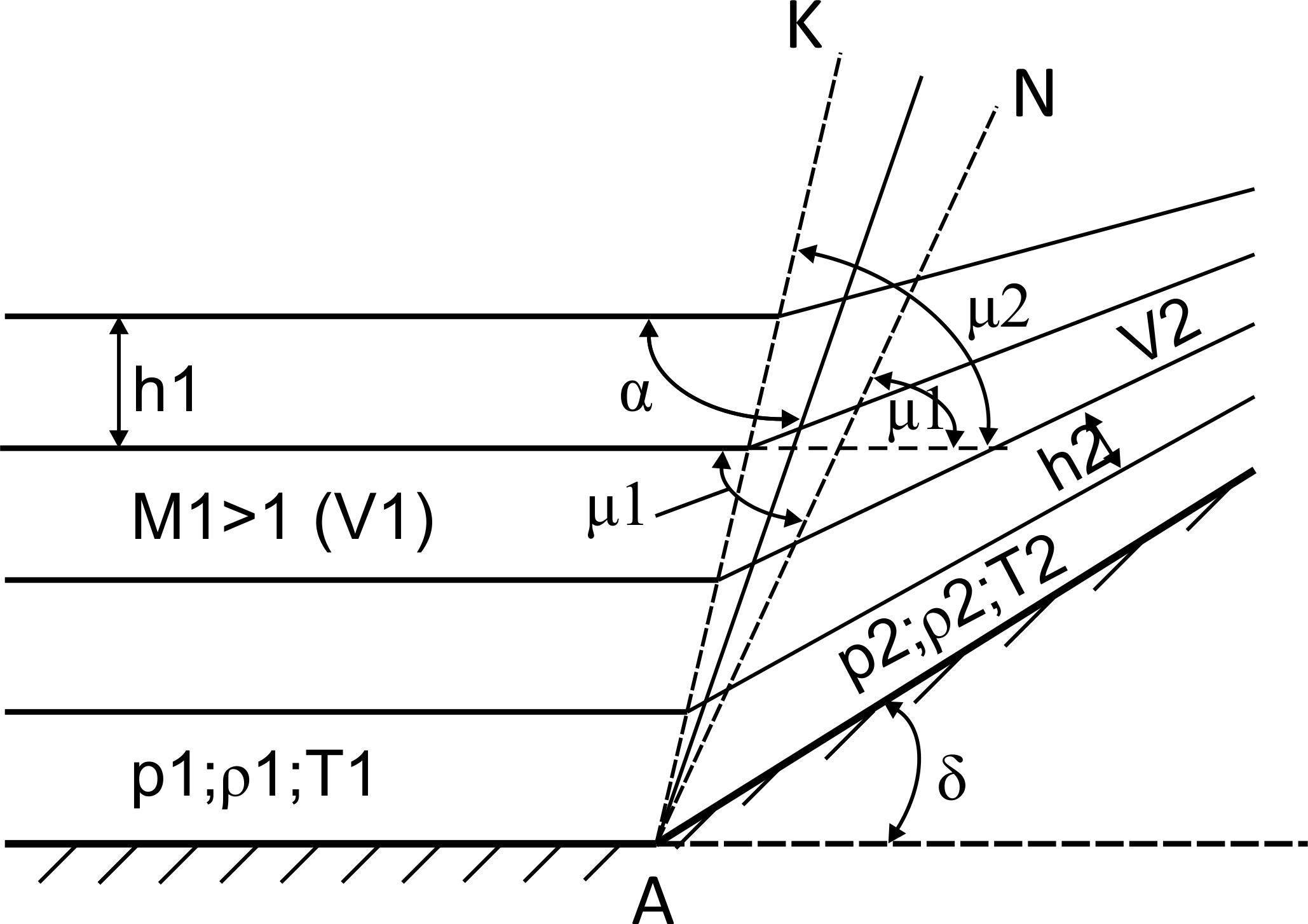
Анализ данного случая с позиций рассмотренного выше неразрывного течения (течение Прандтля-Майера) здесь неприменим.

Рис. 2.6 Возникновение скачка уплотнения при торможении сверхзвукового потока

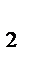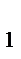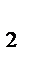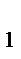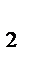Для анализа изменения угла Маха используем уравнение (2.1), которое показывает: угол Маха m за областью поворота увеличивается по отношению к соответствующему углу m перед областью поворота (М < М => m >m ).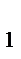

Простой геометрический анализ углов 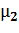и 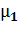показывает, что конечная линия поворота АК оказывается перед начальной NА. Такого в природе быть не может, поэтому между вышеназванными линиями поворота возникает разрыв потока, который, собственно, и является скачком уплотнения. Здесь α – угол между набегающим потоком и СУ; δ - угол поворота в скачке. Если α = 90°, то СУ – прямой. Если α <90°, то СУ – косой.

Уравнение Гюгонио в случае сужения сверхзвукового потока показывает, что скорость в отдельных струйках уменьшается. Сужение определяется поворотом (угол поворота δ) потока после прохождения точки А: расстояние h между струйками уменьшается .

С учетом известного уравнения энергии мы можем утверждать, что термодинамические параметры p, r и T при обтекании внешнего тупого угла увеличиваются (скорость и температура в уравнении энергии обратно пропорциональны). Причем, все изменения осуществляются резко, скачком.

Таким образом, скачок уплотнения это - разрыв газового потока, в котором скорость сверхзвукового потока резко, скачком уменьшается, а термодинамические параметры также скачком увеличиваются.