Функции нескольких переменных
При рассмотрении функций нескольких переменных ограничимся подробным описанием функций двух переменных, т.к. все полученные результаты будут справедливы для функций произвольного числа переменных.
Определение: Если каждой паре независимых друг от друга чисел (х, у) из некоторого множества по какому - либо правилу ставится в соответствие одно или несколько значений переменной z, то переменная z называется функцией двух переменных.
z = f(x, y)
Определение: Если паре чисел (х, у) соответствует одно значение z, то функция называется однозначной, а если более одного, то – многозначной.
Определение: Областью определения функции z называется совокупность пар (х, у), при которых функция z существует.
Определение: Окрестностью точкиМ0(х0, у0) радиуса r называется совокупность всех точек (х, у), которые удовлетворяют условию 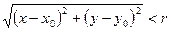 .
.
Определение: Число А называется пределом функции f(x, y) при стремлении точки М(х, у) к точке М0(х0, у0), если для каждого числа e > 0 найдется такое число r >0, что для любой точки М(х, у), для которых верно условие
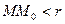
также верно и условие 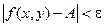 .
.
Записывают: 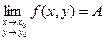
Определение: Пусть точка М0(х0, у0) принадлежит области определения функции f(x, y). Тогда функция z = f(x, y) называется непрерывной в точке М0(х0, у0), если
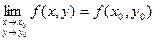 (1)
(1)
причем точка М(х, у) стремится к точке М0(х0, у0) произвольным образом.
Если в какой – либо точке условие (1) не выполняется, то эта точка называется точкой разрывафункции f(x, y). Это может быть в следующих случаях:
1) Функция z = f(x, y) не определена в точке М0(х0, у0).
2) Не существует предел 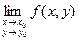 .
.
3) Этот предел существует, но он не равен f( x0, y0).
Свойство. Если функция f(x, y) определена и непрерывна в замкнутой и ограниченной области D, то в этой области найдется по крайней мере одна точка N(x0, y0такая, что для остальных точек верно неравенство
f(x0, y0) ³ f(x, y)
а также точка N1(x1, y1), такая, что для всех остальных точек верно неравенство
f(x1, y1) £ f(x, y)
тогда f(x0, y0) = M – наибольшее значение функции, а f(x1, y1) = m – наименьшее значениефункции f(x, y) в области D.
Непрерывная функция в замкнутой и ограниченной области D достигает по крайней мере один раз наибольшего значения и один раз наименьшего.
Свойство. Если функция f(x, y) определена и непрерывна в замкнутой ограниченной области D, а M и m – соответственно наибольшее и наименьшее значения функции в этой области, то для любой точки m Î [m, M] существует точка
N0(x0, y0) такая, что f(x0, y0) = m.
Проще говоря, непрерывная функция принимает в области D все промежуточные значения между M и m. Следствием этого свойства может служить заключение, что если числа M и m разных знаков, то в области D функция по крайней мере один раз обращается в ноль.
Свойство. Функция f(x, y), непрерывная в замкнутой ограниченной области D, ограничена в этой области, если существует такое число К, что для всех точек области верно неравенство 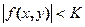 .
.
Приведенные выше свойства аналогичны свойствам функций одной переменной, непрерывных на отрезке.
