Место и роль математического моделирования в задачах исследования, проектирования и оптимизации технологических систем

Лекция 1. Введение в моделирование

План лекции

1. Объект моделирования.

2. Основные понятия и определения.

3. Классификация процессов как объектов моделирования.

4. Постановка задачи моделирования в общем виде.

Объект моделирования

Объектом называется все, на что направлена человеческая деятельность. Выработка методологии управления объектами ориентирована на упорядочение получения и обработки информации об объектах, которые существуют вне нашего сознания и взаимодействуют между собой и внешней средой.

Научно-техническое развитие в любой области обычно идет по следующему пути: сначала ведутся наблюдения и ставятся эксперименты, затем выполняются теоретические исследования и, наконец, осуществляется организация производственных процессов. Такой подход дает возможность получить целостное представление об объекте моделирования и выработать рекомендации по управлению технологической системой, позволяющие оптимизировать технологический процесс.

Основные понятия и определения

В наиболее общем смысле теория математического моделирования (ММ) и оптимизации представляет собой совокупность фундаментальных математических результатов и численных методов, ориентированных на нахождение и идентификацию наилучших вариантов из множества альтернатив и позволяющих избежать полного перебора и оценки возможных вариантов. Например, необходимо построить цех по производству никеля. Это может быть реализовано путем строительства как электропечей, так и печей жидкой ванны (ПЖВ) различной мощности. Задача заключается в выборе еще на стадии проектирования наилучшего варианта из возможных. Процесс оптимизации лежит в основе всей инженерной деятельности, т.к. позволяет, с одной стороны, проектировать новые более эффективные и менее дорогостоящие технические системы и, с другой стороны, разрабатывать методы повышения качества функционирования существующих систем.

В теории моделирования и оптимизации нашли широкое применение следующие понятия.

Определение 1.1.Гипотезой называется определенное предсказание, основывающееся на небольшом количестве опытных данных, наблюдений.

Так, небольшое количество экспериментальных данных, полученных на промышленных рудно-термических печах (РТП), позволяет предположить возможность использования напряженности магнитного поля Н_м, наведенного с наружной стороны электропечи, для контроля уровня расплавов в ней. При формулировании и проверке правильности гипотез большое значение в качестве метода суждения может быть использована аналогия.

Определение 1.2.Аналогией называется суждение о каком-либо частном сходстве двух объектов.

Причем такое сходство может быть существенным и несущественным. В частности, в качестве аналогии можно рассмотреть дуговые электропечи для плавки черных металлов и электрокорунда. Данные печи обладают тем частным свойством, что для плавления шихты в них используется электрическая дуга трехфазного тока. Гипотезы и аналогии должны обладать наглядностью и сводиться к удобным для исследования логическим схемам или моделям.

Определение 1.3.Строго говоря, моделью называется записанная на определенном языке (естественном, математическом и др.) совокупность знаний, представлений и гипотез об объекте или явлении. Соответственно, моделирование – это замещение одного объекта другим с целью получения информации о важнейших свойствах объекта-оригинала с помощью объекта-модели.

В качестве модели можно рассмотреть «холодную» модель электролизера, в которой вместо расплава электролита используют раствор электролита. Такие модели с успехом применяют для исследования электрических ре- жимов электролизеров, а также токораспределения в ванне электролизера или рудно-термической электропечи.

Определение 1.4.Адекватность модели объекту есть показатель того, что результаты моделирования подтверждаются и могут служить основой для прогнозирования процессов, протекающих в исследуемых объектах.

Адекватность модели зависит от целей моделирования и принятых критериев. Учитывая заложенную при создании неполноту модели, можно утверждать, что идеально адекватная модель принципиально невозможна.

Место и роль математического моделирования в задачах исследования, проектирования и оптимизации технологических систем

Для изучения и оптимизации существующих и проектирования вновь разрабатываемых технологических систем их необходимо представить в виде, удобном для исследования. С этой целью техническую систему упрощают. Такую систему (или ее часть), называемую системой автоматического управления (СУ), можно представить состоящей из двух частей: объекта управления (ОУ) и устройства управления (УУ) (рис. 1.1, а). На рис. 1.1, б представлен пример системы управления процессом плавки в РТП.

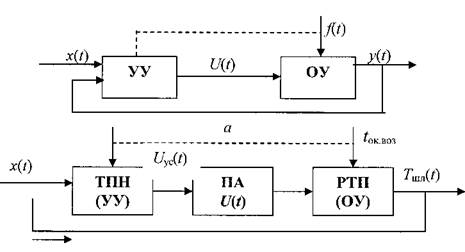
Рис. 1.1. Структурная схема системы автоматического моделирования

а – в общем виде; б – система автоматического управления электрическим режимом РТП

Здесь ТПН – это тиристорный преобразователь напряжения; ПА – перемещение электрода; x(t) – входное воздействие; y(t) – выход системы, ОУ; U_ус(t) – управляющее воздействие; f(t) – случайные возмущения; РТП – рудно-термическая печь; Т_шл (t) – температура шлака; t_ок.воз – случайное возмущение температуры окружающего воздуха.

Под ОУ применительно к задачам инженерии подразумевается техническое устройство, процессом y(t) на выходе которого надлежит управлять, УУ обобщает все входящие в контур СУ элементы, используемые с целью организации процесса управления. На вход системы управления подается воздействие x(t), определяющее желаемый характер управляемого процесса y(t), УУ на основании информации о процессах x(t) и y(t), а в ряде случаев и на основании данных о возмущениях f(t), рассчитывает управляющее воздействие U(t) на объект с целью приведения процесса y(t) в соответствие с сигналом x(t).

Для решения большинства задач анализа и синтеза СУ необходимо иметь математическую модель ОУ. Построение математической модели заключается в установлении ряда соотношений, позволяющих при каждых входных воздействиях и начальных состояниях найти сигнал на выходе ОУ. Обычно модель получают как математическую формулировку физических законов, которым подчинена работа ОУ. В общем случае ОУ является многомерным и имеет l управляемых процессов – у₁(t), у₂(t), …, у_l(t), m управляющих воздействий – u₁(t), u₂(t), …, u_m(t), k внешних возмущений – f₁(t), f₂(t),…, f_k(t) (рис. 1.2).

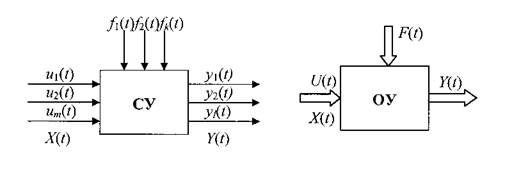
Рис. 1.2. Структурная схема управления объектом моделирования

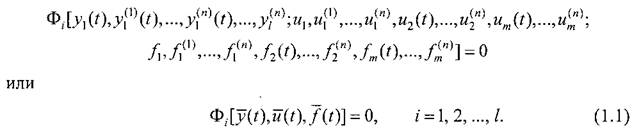Математическая запись физических законов, определяющих свойства непрерывного объекта, в большинстве случаев может быть представлена как система нелинейных дифференциальных уравнений, связывающих входные и выходные процессы и их производные:

При l = 1 объект называют одномерным.

Если функции Φ_i являются линейными относительно управляемых и управляющих процессов и их производных, то объект называют линейным по управлению, аналогично линейным по возмущению.

Математическая модель (1.1) в современной теории оптимальных и адаптивных систем получила ограниченное распространение. Гораздо чаще дифференциальные уравнения (1.1) n-го порядка представляют в виде системы из nl дифференциальных уравнений первого порядка, разрешенных относительно производных.