Основні методи інтегрування функцій

Застосування основних властивостей невизначеного інтеграла, а також табличних інтегралів складають основу метода безпосереднього інтегрування.

Приклад 5. Обчислити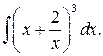

Врахуємо, що 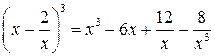. Звідси, на підставі властивостей 4, 5 й табличних інтегралів 1. і 2., матимемо

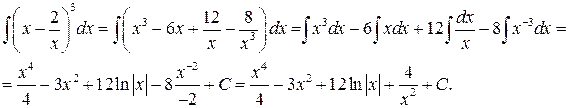
Приклад 6. Обчислити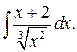

Зауважимо спочатку, що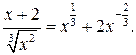

Звідси, на підставі властивостей 4 і 5 й табличного інтеграла 1., матимемо

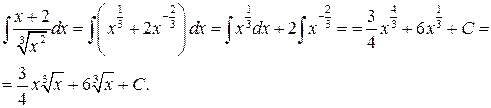
Приклад 7.Обчислити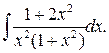

Ураховуючи, що 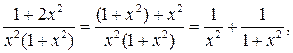на підставі властивості 5 й табличних інтегралів 1. і 3. матимемо

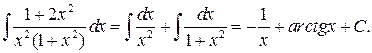
Приклад 8. Обчислити 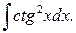Зауважимо, що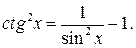

Звідси, на підставі властивості 5 й табличних інтегралів 1. і 11., матимемо

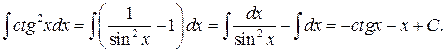
Як бачимо, мистецтво інтегрування полягає в умінні за допомогою властивостей невизначеного інтеграла перетворити підінтегральний вираз на „табличний”. Потрібно домогтися, щоб він став таким, як в одному із табличних інтегралів, або спочатку хоча б спростився. Для цього, крім методу безпосереднього інтегрування, застосовують інші методи.

У багатьох випадках введення нової змінної інтегрування дає змогу звести обчислення даного інтеграла до знаходження табличного інтеграла. Цей спосіб називають методом заміни змінної або методом підстановки. Він базується на такій теоремі.

Теорема. Нехай функція 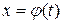визначена й диференційовна на проміжку Т, а проміжок Х –множина її значень. Нехай функція 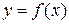визначена на проміжку Х і має на ньому первісну 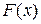. Тоді на проміжку Т складена функція 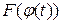є первісною функції 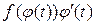, тобто

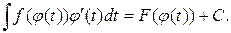(25)

Доведення. Згідно з правилом диференціювання складеної функції, враховуючи, що 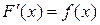, дістанемо

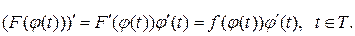
Отже, функція 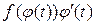дійсно має на проміжку Т однією зі своїх первісних функцію 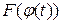, тобто виконується співвідношення (25).

Оскільки 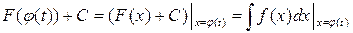, то рівність (25) можна подати у вигляді

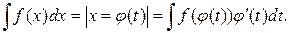(26)

Рівність (26) називають формулою заміни змінної в невизначеному інтегралі.

Приклад 9.Обчислити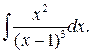

У підінтегральній функції зробимо заміну: 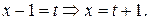Вважаючи, що х і t – незалежні змінні, встановимо зв’язок між диференціалами: 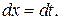Заміну і деякі наслідки, що з неї випливають, як правило, записують після інтеграла, який обчислюється, між двома вертикальними лініями:

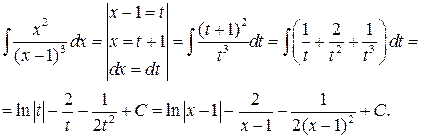
Приклад 10.Обчислити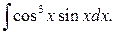

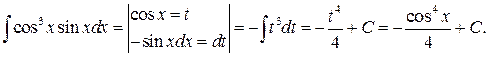
Приклад 11.Обчислити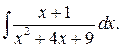

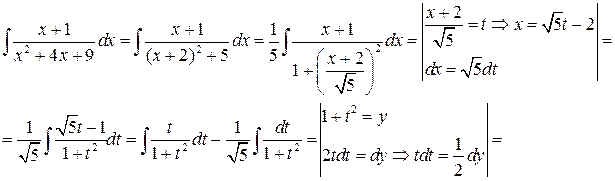
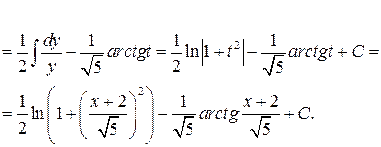
Приклад 12.Обчислити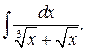

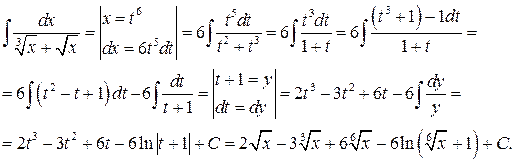
Приклад 13.Обчислити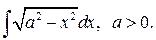

Зручно зробити заміну 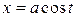, оскільки 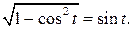Отже, маємо:

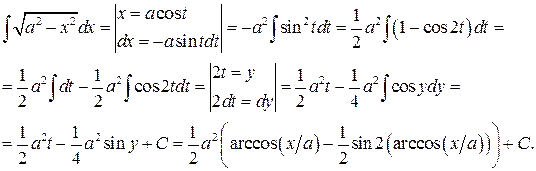
Приклад 14. Обчислити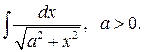

Введемо спочатку такі гіперболічні функції:

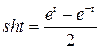(гіперболічний синус),

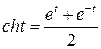(гіперболічний косинус).

Легко перевірити, що

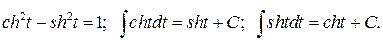
У підінтегральній функції зручно зробити таку заміну: 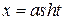, оскільки 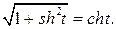Тоді маємо:

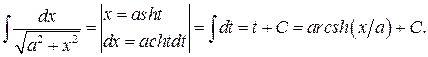
Приклад 15.Обчислити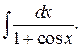

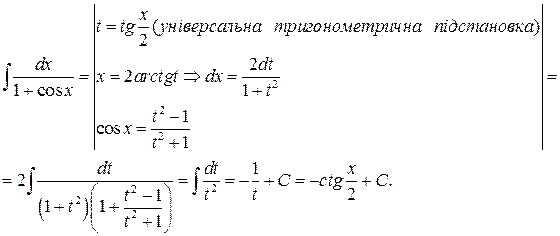
Метод інтегрування за частинами.Нехай функції и(х) і v(x) визначені і диференційовні на деякому проміжку Х. Тоді справедлива така формула (формула інтегрування частинами):

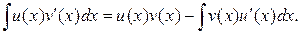(27)

Приклад 16.Обчислити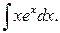

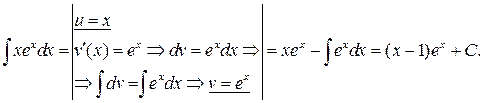
Приклад 17.Обчислити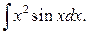

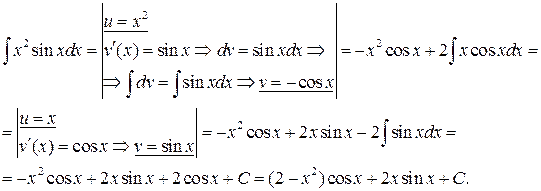
Метод невизначених коефіцієнтів. Нехай дробово-раціональна функція 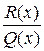має степінь многочлена в чисельнику менший за степінь многочлена у знаменнику. Многочлен 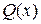має такий вигляд:

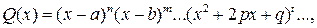де 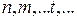– цілі числа і 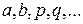– дійсні числа. Тоді дробово-раціональну функцію 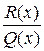можна єдиним чином представити у вигляді:

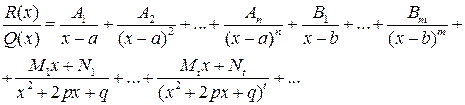(28)

Вираз (28) називається розкладом дробово-раціональної функції на прості дроби. Дійсні числа 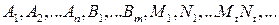– невідомі коефіцієнти цього розкладу.

Приклад 18. Обчислити інтеграл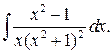

Розкладемо спочатку підінтегральну функцію на прості дроби. Згідно з формулою (28) маємо:

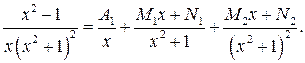
Знайдемо невідомі коефіцієнти розкладу, для чого перемножимо ліву і праву частину рівності на :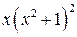

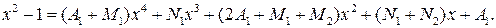
Прирівнюючи далі коефіцієнти, які стоять при однакових степенях х ліворуч і праворуч рівності, отримуємо таку систему лінійних алгебраїчних рівнянь:

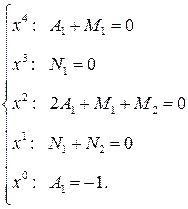
Розв’язуючи її, знаходимо: 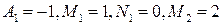і 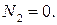Отже, шуканий розклад є таким:

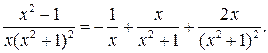
Після цього обчислюємо інтеграл: