Векторы и действия над ними
В геометрии под вектором (в узком смысле слова) понимается всякий направленный отрезок. Вектор с началом в точке A и концом в точке B принято обозначать символом 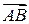 . Часто векторы обозначают одной буквой, например,
. Часто векторы обозначают одной буквой, например, 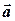 . Векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Векторы называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. К линейным операциям над векторами относят операции сложения и вычитания векторов, а также умножение вектора на число.
. Векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Векторы называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. К линейным операциям над векторами относят операции сложения и вычитания векторов, а также умножение вектора на число.
Пример 2.1. По двум заданным векторам 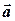 и и 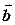 построить векторы построить векторы 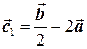 и и 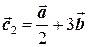 , если , если 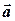 и и 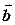 приведены на рисунке. приведены на рисунке. |
|
Решение. Чтобы сложить векторы, нужно совместить параллельным переносом начало и конец этих векторов. Тогда суммой этих векторов будет вектор, соединяющий начало первого и конец второго вектора (правило треугольника). Векторы можно сложить также по правилу параллелограмма, совместив начала этих векторов. Суммой векторов, в этом случае, будет диагональ параллелограмма, выходящая из начала векторов.
Разностью 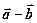 двух векторов
двух векторов 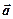 и
и 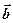 называется сумма
называется сумма 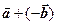 , т.е. чтобы вычесть из вектора
, т.е. чтобы вычесть из вектора 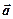 вектор
вектор 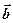 , достаточно прибавить к вектору
, достаточно прибавить к вектору 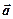 вектор (–
вектор (– 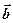 ). Отметим, что если на векторах
). Отметим, что если на векторах 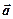 и
и 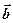 построить параллелограмм, то одна его диагональ равна сумме
построить параллелограмм, то одна его диагональ равна сумме  , а вторая – разности
, а вторая – разности 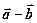 .
.
|
|
| |||||||||
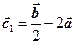 | 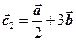 |
Система векторов 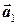 ,
, 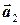 , ... ,
, ... , 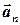 называется линейно зависимой, если найдется хотя бы одно не равное нулю число k1, k2 , ... , kn, чтобы выполнялось равенство
называется линейно зависимой, если найдется хотя бы одно не равное нулю число k1, k2 , ... , kn, чтобы выполнялось равенство 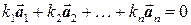 . Если данное равенство может выполняться только при условии, что все числа k1, k2 , ... , kn равны нулю, то такая система векторов называется линейно независимой. В частности, любые два коллинеарных вектора линейно зависимы; любые три компланарных вектора линейно зависимы; любые четыре 3-х мерных вектора линейно зависимы.
. Если данное равенство может выполняться только при условии, что все числа k1, k2 , ... , kn равны нулю, то такая система векторов называется линейно независимой. В частности, любые два коллинеарных вектора линейно зависимы; любые три компланарных вектора линейно зависимы; любые четыре 3-х мерных вектора линейно зависимы.
Линейно-независимые векторы образуют базис для какого-либо множества векторов, если любой вектор из этого множества может быть представлен в виде некоторой линейной комбинации исходных векторов.
Пусть какая-нибудь тройка векторов  образует базис в пространстве. Тогда любой вектор пространства можно разложить и притом единственным образом по этому базису:
образует базис в пространстве. Тогда любой вектор пространства можно разложить и притом единственным образом по этому базису:
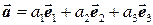 . (2.1)
. (2.1)
Числа a1, a2, a3 называются координатами вектора 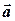 в базисе векторов
в базисе векторов  , что обозначается
, что обозначается 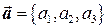 . Значение координат состоит в том, что операции над векторами можно сводить к действиям над числами. Тогда при сложении векторов будут складываться их соответствующие координаты, при умножении вектора на число все его координаты умножаются на это число и т.д.
. Значение координат состоит в том, что операции над векторами можно сводить к действиям над числами. Тогда при сложении векторов будут складываться их соответствующие координаты, при умножении вектора на число все его координаты умножаются на это число и т.д.
Два ненулевых вектора 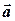 и
и 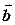 коллинеарны тогда и только тогда, когда выполняется равенство
коллинеарны тогда и только тогда, когда выполняется равенство 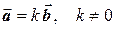 . Если векторы заданы в координатной форме, то условие коллинеарности будет иметь вид
. Если векторы заданы в координатной форме, то условие коллинеарности будет иметь вид
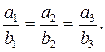 (2.2)
(2.2)
Пример 2.2. Коллинеарны ли векторы 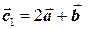 и
и 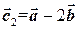 , если
, если 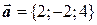 и
и 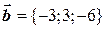 .
.
Решение. Найдем координаты векторов 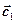 и
и 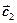 :
:
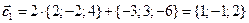 ,
,
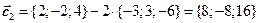 .
.
Из условия пропорциональности
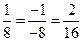 .
.
заключаем, что векторы 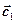 и
и 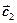 коллинеарны, причем
коллинеарны, причем 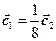 .
.
Пример 2.3. Показать, что векторы 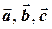 образуют базис. Найти разложение вектора
образуют базис. Найти разложение вектора 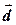 по этому базису, если
по этому базису, если 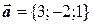 ,
, 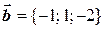 ,
, 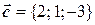 ,
, 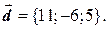
Решение. Векторы 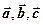 образуют базис, если определитель, составленный из координат этих векторов (смешанное произведение векторов) не равен нулю. Поскольку
образуют базис, если определитель, составленный из координат этих векторов (смешанное произведение векторов) не равен нулю. Поскольку
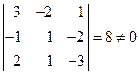 ,
,
то векторы 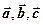 образуют базис. Следовательно, вектор
образуют базис. Следовательно, вектор 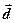 можно разложить по этому базису:
можно разложить по этому базису:
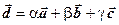 .
.
Найдем числа a, b, g. Для этого векторное уравнение распишем по координатам:
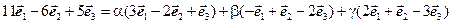 ,
,
или
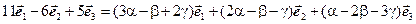 .
.
Два вектора равны, если равны их соответствующие координаты. Отсюда получаем систему уравнений:
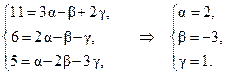
Таким образом, искомое разложение имеет вид
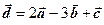 .
.
Ортонормированный базис – это базис, состоящий из единичных (нормированных) и взаимно перпендикулярных (ортогональных) векторов. В этом случае базисные вектора имеют особые обозначения: 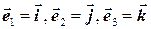 . Координаты вектора в таком базисе обычно обозначаются буквами x, y, z:
. Координаты вектора в таком базисе обычно обозначаются буквами x, y, z: 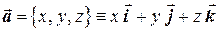 . Длина вектора в ортонормированном базисе равна
. Длина вектора в ортонормированном базисе равна
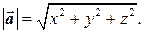 (2.3)
(2.3)