Линейные операторы и функционалы в пространстве финитных функций
Финитные функции.
Пусть 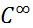 - пространство всех бесконечно дифференцируемых функций на всей числовой оси.
- пространство всех бесконечно дифференцируемых функций на всей числовой оси.
Опр.Функция 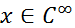 наз-ся финитной слева, если сущ-т такое число a, что для всех
наз-ся финитной слева, если сущ-т такое число a, что для всех 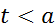 имеем
имеем 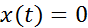 . Совокупность всех финитных слева функций обозначается
. Совокупность всех финитных слева функций обозначается 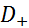 . Свойства финитных слева функций:
. Свойства финитных слева функций:
1. Произведение любого числа и финитной слева функции является финитной слева функцией, то есть если 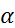 – произвольное число и
– произвольное число и 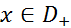 , то
, то 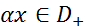
2. Сумма конечного числа финитных слева функций является финитной слева функцией, то есть если 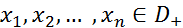 , то
, то
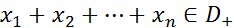
3. Произведение конечного числа бесконечно дифференцируемых функций, одна из которых финитна слева, является финитной слева функцией, то есть если 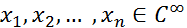 и существует такое
и существует такое 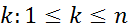 , что
, что 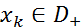 , то
, то 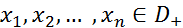
4. Из свойств 1 и 2 следует, что 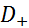 - векторное пространство пространства
- векторное пространство пространства 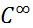 , и тогда из свойства 3 получаем, что
, и тогда из свойства 3 получаем, что 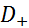 - подалгебра алгебры
- подалгебра алгебры 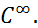
Пример: 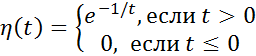 . График:
. График: 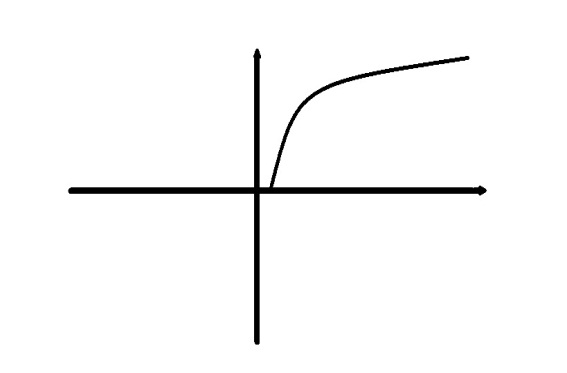 Докажем что
Докажем что 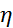 - бесконечно дифференцируема. Для этого достаточно показать, что она бесконечно дифференцируема в точке
- бесконечно дифференцируема. Для этого достаточно показать, что она бесконечно дифференцируема в точке 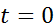 . Имеем
. Имеем 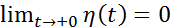 и
и 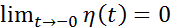 и, следовательно, функция
и, следовательно, функция 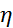 непрерывна. Далее имеем:
непрерывна. Далее имеем: 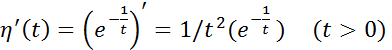 и применяя правило Лопиталя, получим
и применяя правило Лопиталя, получим 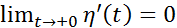 и
и 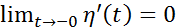 , то ф-ция
, то ф-ция 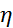 дифференцируема в точке
дифференцируема в точке 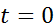 , причём
, причём 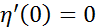 . Дифференцируя ф-цию
. Дифференцируя ф-цию 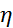 при
при  несколько раз, можно прийти в заключению, что её -ая производная выражается формулой:
несколько раз, можно прийти в заключению, что её -ая производная выражается формулой: 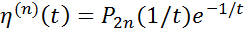
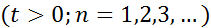 , где
, где 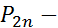 полином степени
полином степени 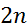 .
.
Из формулы (1) следует, что 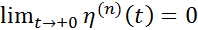 при
при 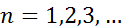 и
и 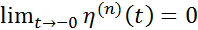 при
при 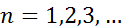 , то сущ-т -ая производная функции
, то сущ-т -ая производная функции 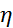 в точке
в точке 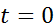 для любого натурального числа
для любого натурального числа 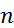 , то есть функция
, то есть функция 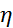 бесконечно дифференцируема в точке
бесконечно дифференцируема в точке 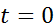 , что и требовалось доказать. Опр.Функция
, что и требовалось доказать. Опр.Функция 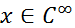 наз-ся финитной справа, если сущ-т такое число
наз-ся финитной справа, если сущ-т такое число 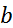 , что для всех
, что для всех  имеем
имеем 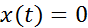 . Обозначается
. Обозначается 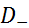 . Множество финитных справа функций обладает теме же свойствами, что и множество финитных слева функций. Пример финитной справа функции:
. Множество финитных справа функций обладает теме же свойствами, что и множество финитных слева функций. Пример финитной справа функции: 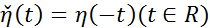 . График:
. График:
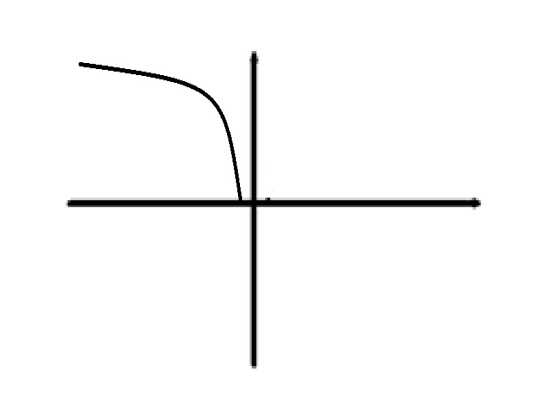
Опр.Функция 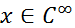 наз-ся финитной, если она финитна слева и финитна справа, то есть сущ-т такие числа
наз-ся финитной, если она финитна слева и финитна справа, то есть сущ-т такие числа 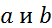 , что для всех
, что для всех 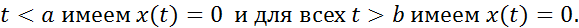 Опр.Функция
Опр.Функция 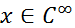 наз-ся финитной, если сущ-т такой отрезок
наз-ся финитной, если сущ-т такой отрезок 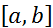 , вне которого функция обращается(тождественно) в нуль, то есть для всех
, вне которого функция обращается(тождественно) в нуль, то есть для всех 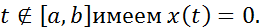 Опр.Функция
Опр.Функция 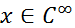 наз-ся финитной, если сущ-т такое ограниченное множество на числовой оси, вне которого функция обращается в нуль.Финитная функция обозначается
наз-ся финитной, если сущ-т такое ограниченное множество на числовой оси, вне которого функция обращается в нуль.Финитная функция обозначается 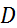 .Носителем функции
.Носителем функции 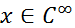 называется замыкание множества тех точек числовой прямой,в которых функция не обращается в нуль. Обозначения носителя функции х: supp x. Примеры:1.supp
называется замыкание множества тех точек числовой прямой,в которых функция не обращается в нуль. Обозначения носителя функции х: supp x. Примеры:1.supp 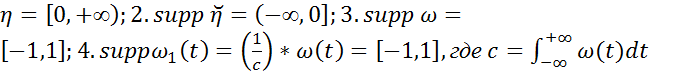
Критерий финитности функций. Пусть 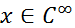 . Тогда справедливы следующие утверждения:
. Тогда справедливы следующие утверждения:
1. Для того чтобы функция х была финитной слева, необходимо и достаточно чтобы её носитель был ограничен слева, т.е. 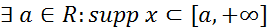
2. Для того чтобы функция х была финитной справа, необходимо и достаточно чтобы её носитель был ограничен справа, т.е. 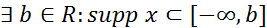
3. Для того чтобы функция х была финитной, необходимо и достаточно чтобы её носитель был компактным множеством.
Свертка финитных функций
При умножении двух функций, представл. рядами Лорана
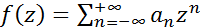 и
и 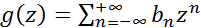
получаем произведение функций, также представляемое рядом Лорана 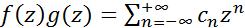 , коэффициенты которого
, коэффициенты которого 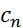 связаны с коэффициентами
связаны с коэффициентами 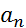 и
и 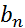 следующим образом:
следующим образом:
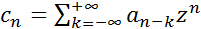 (1)
(1)
Последовательность 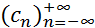 , определяемая формулой (1), называется свёрткой последовательностей
, определяемая формулой (1), называется свёрткой последовательностей 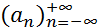 и
и 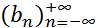 .
.
Рассмотрим две функции, представленные в виде интегралов Лапласа
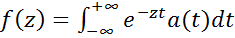 ,
, 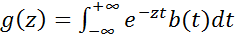
Перемножая эти функции и проводя формальные преобразования, получаем
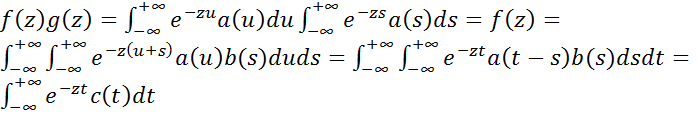 ,
,
где 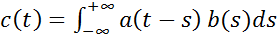 , (
, ( 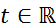 )(2)
)(2)
Функция 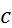 , определенная формулой (2), называется сверткой функций
, определенная формулой (2), называется сверткой функций 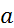 и
и 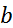 и обозначается
и обозначается 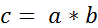 .
.
Бинарная операция  называется операцией свертки, или просто сверткой.Заменой переменных в правой части формулы (2) получим
называется операцией свертки, или просто сверткой.Заменой переменных в правой части формулы (2) получим 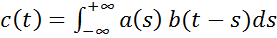 , (
, ( 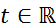 ) (3)
) (3)
откуда следует, что 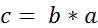 .Из равенств
.Из равенств 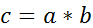 и
и 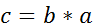 имеем
имеем 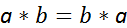 .Это означает, что свертка коммутативна.
.Это означает, что свертка коммутативна.
Свертка также обладает, как легко следует из линейности интеграла, следующими алгебраическими свойствами:
1) 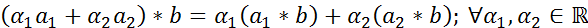
2) 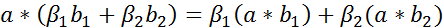 ;
; 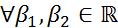
Свойство 1) называется линейностью свертки по первому аргументу, а свойство 2) - линейностью по второму аргументу.
Бинарная операция, обладающая свойствами 1) и 2), называется билинейной. Таким образом, свертка билинейна.
Теорема 1 (о свертке финитных слева функций). Пусть 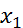 ,
, 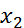 - финитные слева функции. Тогда:1) свертка
- финитные слева функции. Тогда:1) свертка 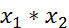 , существует и является финитной слева функцией, причем, если
, существует и является финитной слева функцией, причем, если 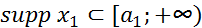 и
и 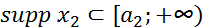 , то
, то 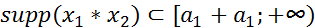 ;
;
2) для любого натурального числа 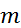 справедливо равенство
справедливо равенство 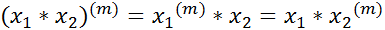 .
.
Следствие. Векторное пространство 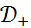 относительно введенной операции свертки является коммутативной алгеброй.
относительно введенной операции свертки является коммутативной алгеброй.
В этом случае мы будем говорить, что 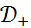 - сверточная алгебра.
- сверточная алгебра.
Обозначим через 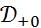 множество всех финитных слева функций, носители которых содержатся на замкнутой полуоси
множество всех финитных слева функций, носители которых содержатся на замкнутой полуоси 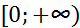 . Тогда, как следует из теоремы,
. Тогда, как следует из теоремы, 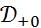 - подалгебра сверточной алгебры
- подалгебра сверточной алгебры 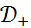 .
.
Теорема 2(о свертке финитных справа функций). Пусть 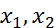 - финитные справа функции. Тогда
- финитные справа функции. Тогда
1) свертка 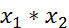 существует и является финитной справа
существует и является финитной справа
функцией, причем, если 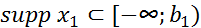 и
и
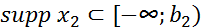 , то
, то 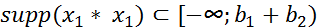 .
.
2) для любого натурального числа m справедливо равенство 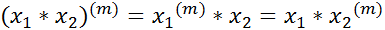 .
.
Следствие. 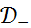 - сверточная алгебра.
- сверточная алгебра.
Обозначим через 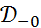 множество всех финитных справа функций, носители которых содержатся на замкнутой полуоси
множество всех финитных справа функций, носители которых содержатся на замкнутой полуоси 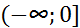 . Тогда, как следует из теоремы,
. Тогда, как следует из теоремы, 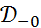 - подалгебра сверточной алгебры
- подалгебра сверточной алгебры 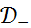 .
.
Теорема 3 (о свертке финитных функций). Пусть 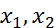 - финитные функции. Тогда
- финитные функции. Тогда
1) свертка 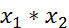 существует и является финитной функцией, причем, если
существует и является финитной функцией, причем, если 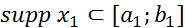 и
и 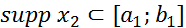 , то
, то 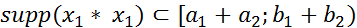
2) для любого натурального числа 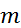 справедливо равенство
справедливо равенство
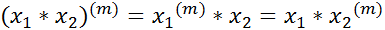 .
.
Следствие.  - сверточная алгебра.
- сверточная алгебра.
Таким образом, 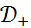 ,
, 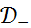 ,
,  являются одновременно и мультипликативными алгебрами, и сверточными алгебрами.
являются одновременно и мультипликативными алгебрами, и сверточными алгебрами.
Линейные операторы и функционалы в пространстве финитных функций.
Сформулируем необходимое и достаточное условие непрерывности линейного функционала на пространстве  .
.
Теорема 1 (критерий непрерывности линейного функционала на пространстве  ).
).
Линейный функционал на пространстве  непрерывен тогда и только тогда, когда он непрерывен на любом подпространстве
непрерывен тогда и только тогда, когда он непрерывен на любом подпространстве 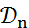 .
.
Доказательство. Пусть f— линейный функционал на пространстве  . В силу определения функционал f непрерывен тогда и только тогда, когда
. В силу определения функционал f непрерывен тогда и только тогда, когда 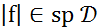 .
.
Тогда, используя определение полинормы 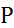 в пространстве
в пространстве  , преднорма
, преднорма 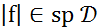 тогда и только тогда, когда сужение преднормы на любом подпространстве
тогда и только тогда, когда сужение преднормы на любом подпространстве 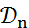 принадлежит
принадлежит 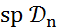 .
.
Но сужение преднормы 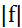 на подпространство
на подпространство 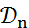 совпадает с модулем функционала, который является сужением функционала f на подпространстве
совпадает с модулем функционала, который является сужением функционала f на подпространстве 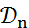 .
.
Таким образом, преднорма 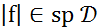 тогда и только тогда, когда
тогда и только тогда, когда
сужение функционала f на любое подпространство 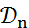 непрерывно, т.е. функционал f непрерывен тогда и только тогда, когда его сужение на любое подпространство
непрерывно, т.е. функционал f непрерывен тогда и только тогда, когда его сужение на любое подпространство 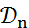 непрерывно, что и требовалось доказать.
непрерывно, что и требовалось доказать. 
Теорема 2 (критерий непрерывности линейного оператора, определенного на пространстве  ).
).
Линейный оператор, отображающий  в полинормированное пространство, непрерывен тогда и только тогда, когда он непрерывен на любом подпространстве
в полинормированное пространство, непрерывен тогда и только тогда, когда он непрерывен на любом подпространстве 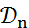 .
.
В качестве примера применения теоремы 2 рассмотрим оператор дифференцирования 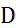 , определенный на всем пространстве
, определенный на всем пространстве  следующим образом:
следующим образом: 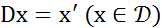 .
.
Очевидно, что 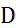 — линейный оператор, отображающий пространство
— линейный оператор, отображающий пространство  в пространство
в пространство  . Докажем его непрерывность. Зафиксируем
. Докажем его непрерывность. Зафиксируем 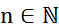 и рассмотрим сужение оператора
и рассмотрим сужение оператора 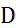 на подпространстве
на подпространстве 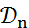 .
.
Тогда для любого 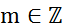 и любого
и любого 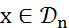 имеем:
имеем: 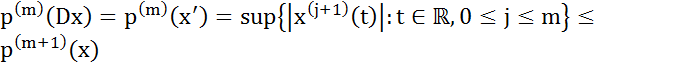 ,
,
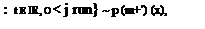 откуда следует, что
откуда следует, что 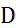 — непрерывный оператор, действующий
— непрерывный оператор, действующий  в
в  . Следовательно, применяя теорему, получим, что оператор
. Следовательно, применяя теорему, получим, что оператор 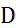 является непрерывным оператором из
является непрерывным оператором из  в
в  .
.
Теорема 3 (секвенциальный критерий непрерывности линейного функционала на пространстве  ).
).
Линейный функционал f на пространстве  непрерывен тогда и только тогда, когда для любой последовательности
непрерывен тогда и только тогда, когда для любой последовательности 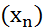 , сходящейся к нулю в пространстве
, сходящейся к нулю в пространстве  , числовая последовательность
, числовая последовательность 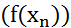 сходится к нулю.
сходится к нулю.
Теорема 4 (секвенциальный критерий непрерывности линейного оператора, определенного на 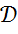 ),Пусть Y - полинормированное пространство.Линейный оператор
),Пусть Y - полинормированное пространство.Линейный оператор 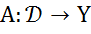 непрерывен тогда и только тогда, когда для любой последовательности
непрерывен тогда и только тогда, когда для любой последовательности 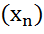 из
из 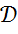 , сходящейся к нулю в пространстве
, сходящейся к нулю в пространстве 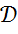 , последовательность
, последовательность 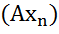 сходится к нулю в пространстве
сходится к нулю в пространстве 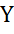 .
.
Теорема 5 (o непрерывности ограниченного линейного оператора на пространстве 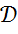 ).Пусть
).Пусть 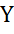 полинормированное пространство.
полинормированное пространство.
Линейный оператор 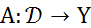 непрерывен тогда и только тогда, когда онограничен.
непрерывен тогда и только тогда, когда онограничен.
Следствие (o непрерывности ограниченного функционала на пространстве  ).
).
Линейный функционал на пространстве  непрерывен тогда и ТОЛЬКО тогда, когда он ограничен.
непрерывен тогда и ТОЛЬКО тогда, когда он ограничен.
Непрерывные линейные функционалы на пространстве  в теории обобщенных функций называются обобщенными функциями.
в теории обобщенных функций называются обобщенными функциями.
Теорема 6(об эквивалентных условиях непрерывности линейного функционала на пространстве  ).
).
Пусть 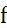 –линейный функционал на пространстве
–линейный функционал на пространстве  .
.
Следующие условия эквивалентны:
1) f непрерывен;
2) f непрерывен на любом подпространстве 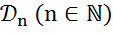 ;
;
3) для любой последовательности 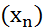 , сходящейся к нулю в пространстве
, сходящейся к нулю в пространстве  , числовая последовательность
, числовая последовательность 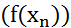 сходится к нулю;
сходится к нулю;
4) f ограничен.
