Решение систем нелинейных уравнений

Рассмотрим решение системы n нелинейных уравнений с n неизвестными:

f₁(x₁, ... ,х_n ) = 0,

. . .

f_n(x₁, ... ,х_n ) = 0,

Для решения систем в MathCad необходимо:

§ задать начальное приближение для всех неизвестных, входящих в систему, на основе которых строится итерационная последовательность уточнений начального приближения, сходящаяся к искомому решению;

§ напечатать ключевое слово Given, которое указывает MathCad, что далее следует система уравнений;

§ ниже слова Given ввести уравнения и неравенства. Для ввода знака равенства между левыми и правыми частями уравнений необходимо использовать клавиатурную комбинацию “Ctrl/=“. Между левыми и правыми частями неравенств могут также стоять знаки: >, <, ;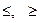

§ ввести любое выражение, которое включает функцию Find ( z₁, z₂ , ...). Число аргументов в этой функции должно быть равно числу неизвестных.

Функция Find возвращает найденное решение следующим образом:

§ если она имеет только один аргумент, то возвращается скаляр, являющийся решением уравнения, расположенного между ключевым словом Given и функцией Find;

§ если Find имеет больше одного аргумента, то она возвращает ответ в виде вектора, содержащего решение системы уравнений.

Ключевое слово Given, уравнения и неравенства, следующие за ним, и выражение, содержащее функцию Find, называются блоком решения уравнений.

В блоке решений недопустимы операторы присваивания, дискретные аргументы, а также выражения, их содержащие, и неравенства вида a < b < c.

Блоки решений не могут быть вложены друг в друга. Каждый блок должен иметь только одно ключевое слово Given и функцию Find.

На рисунке 1.4(а) показан пример блока решения системы трех уравнений с тремя неизвестными. В результате функция Find содержит три аргумента, x , y и z, и возвращает ответ в виде вектора с тремя компонентами.

Функция Find, которая завершает блок решения уравнений, может быть использована аналогично любой другой функции и чаще всего с ней производится одно из следующих действий:

§ можно вывести найденное решение, напечатав выражение вида
Find(z₁, z₂,...)=. Пример того, как это делается для системы двух уравнений с двумя неизвестными, приведен на рисунке 1.4(б);

§ можно определить переменную с использованием этой функции. Для этого в конце блока решения необходимо записать оператор присваивания, слева в котором стоит переменная, а справа функция Find. Пример, иллюстрирующий такую возможность, показан на рисунке 1.4(а);

а) б)

Рисунок 1.4 - Примеры решения систем нелинейных уравнений

§ используя Find, можно определить другую функцию. Для этого необходимо закончить блок решения выражением вида

f(a, b, ...): = Find(z₁, z₂,...).

Эта конструкция удобна при многократном решении системы уравнений для различных значений параметров a, b, ..., непосредственно входящих в систему уравнений. Пример такого использования показан на рисунке 1.5. Определенная в этом примере функция Find для каждого значения параметра R из заданного диапазона возвращает вектор, состоящий из двух элементов, поэтому выводить здесь необходимо раздельно элементы вектора F (R )₀ и F ( R )₁.

Рисунок 1.5 - Пример многократного решения системы

MathCad возвращает в блоке решения уравнений только одно решение системы. Однако, система может иметь несколько решений. Если одно решение найдено, то для поиска других решений можно использовать другие начальные приближения либо ввести дополнительные ограничения в виде неравенств, определяющих нужную область. На рисунке 1.6 показано, как различные начальные приближения дают различные решения задачи, а на рисунке 1.7 - как добавить ограничения в виде неравенств для поиска другого решения.

Рисунок 1.6 - Влияние начальных приближений на решение системы

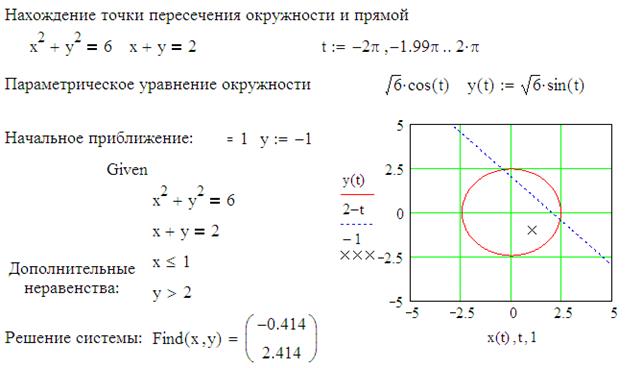Рисунок 1.7 - Ограничения в блоке решения уравнений

Если в результате итерационного процесса не может быть найдено более близкое приближение к искомому решению по сравнению с предыдущим шагом, то поиск решения прекращается, а функция Find помечается сообщением об ошибке.

Причиной появления этого сообщения может быть следующее:

§ задача не имеет решения;

§ для уравнения, которое не имеет вещественных корней, в качестве начального приближения взято вещественное число;

§ в процессе решения получена точка, из которой применяемый MathCad метод минимизации не может определить дальнейшее направление движения. Метод преодоления этой проблемы - изменение начального приближения или добавление ограничений на переменные в виде неравенств, чтобы обойти критическую точку.

В любом случае полезно вывести графики, связанные с системой, которые облегчат поиск области, где находится решение и выбрать подходящее начальное приближение.

Точность решения систем уравнений определяется встроенной константой TOL, изменяя которую можно увеличивать или уменьшать погрешность вычисления корней.