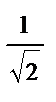Функцияның экстремумдары.
А)Функцияның өсу және кемуініңқажетті және жеткілікті шартары. Анықтама.х0 нүктесінің 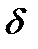 - маңайы табылып, (х0-
- маңайы табылып, (х0- 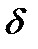 х0+
х0+ 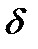 ), осы маңайдағы барлық х
), осы маңайдағы барлық х 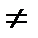 х0 үшін f(x)>f(х0) теңсіздігі орындалса, х0 нүктесі f(x) функциясының минимум нүктесі деп, ал f(x)<f(х0) теңсіздік орындалса, х0 нүктесі f(x) функциясының максимум нүктесі деп аталады. Теорема (функция өсуі мен кемуінің жеткілікті шарты). Егер (а,в) интервалында дифференциалданатын y=f(x) функциясының туындысы оң болса, онда осы интервалда функция өспелі болады, ал туындысы теріс болса, функция кемімелі болады. 1-суреттегі y=f(x) функциясы
х0 үшін f(x)>f(х0) теңсіздігі орындалса, х0 нүктесі f(x) функциясының минимум нүктесі деп, ал f(x)<f(х0) теңсіздік орындалса, х0 нүктесі f(x) функциясының максимум нүктесі деп аталады. Теорема (функция өсуі мен кемуінің жеткілікті шарты). Егер (а,в) интервалында дифференциалданатын y=f(x) функциясының туындысы оң болса, онда осы интервалда функция өспелі болады, ал туындысы теріс болса, функция кемімелі болады. 1-суреттегі y=f(x) функциясы 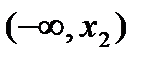 және
және 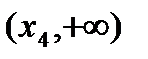 аралығында өседі,
аралығында өседі, 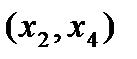 аралығында кемиді.
аралығында кемиді.
у 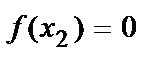 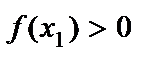 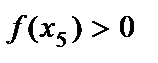 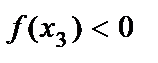 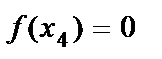 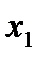 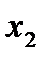 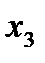 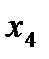 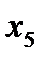 x 1-cурет x 1-cурет |
Б)функция экстремумының қажетті және жеткілікті шартары. Анықтама.Туындысы нолге айналатын не туындысы болмайтын нүктелер функцияның күдікті нүктелері(кейде І-текті күдікті нүктелер) деп аталады. Функцияның минимум және максимум нүктелерінэкстремум нүктелерідеп атайды. Осы нүктелердегі функция мәндерін функция экстремумдарыдейді.
Экстремумның бірінші жеткілікті шарты. y=f(x) функциясы х0 нүктесінде үзіліссіз және қандай да бір 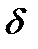 - маңайында функция туындысы бар болсын (х0 нүктесінде туынды болмауы мүмкін). Онда,
- маңайында функция туындысы бар болсын (х0 нүктесінде туынды болмауы мүмкін). Онда,
1) егер х аргумент х0 нүкте арқылы өткенде 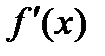 таңбасын оңнан теріске өзгертсе, онда х0 нүкте максимум нүктесі болады;
таңбасын оңнан теріске өзгертсе, онда х0 нүкте максимум нүктесі болады;
2) егер х аргумент х0 нүкте арқылы өткенде 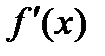 таңбасын терістен оңға өзгертсе, онда х0 нүкте минимум нүктесі болады;
таңбасын терістен оңға өзгертсе, онда х0 нүкте минимум нүктесі болады;
3) егер х аргумент х0нүктеарқылыөткенде 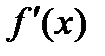 таңбасынөзгертпесе, онда х0 нүкте экстремум нүктесіемес.
таңбасынөзгертпесе, онда х0 нүкте экстремум нүктесіемес.
Экстремумның екінші жеткілікті шарты. y=f(x) функциясы х0 нүктесінде үзіліссіз және қандай да бір 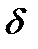 - маңайында екі рет дифференциалдансын. Соныменқатар
- маңайында екі рет дифференциалдансын. Соныменқатар 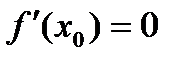
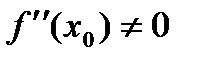 болса, онда
болса, онда
1) егер 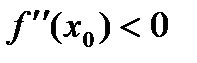 болса, онда х0нүкте f(x) функциясының максимум нүктесіболады;
болса, онда х0нүкте f(x) функциясының максимум нүктесіболады;
2) егер 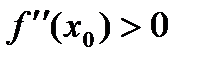 болса, онда х0нүкте f(x) функциясының минимум нүктесіболады.
болса, онда х0нүкте f(x) функциясының минимум нүктесіболады.
19.Функцияны туынды көмегімен зерттеу.
А)Функция графигінің дөңестігі және ойытығы.
Анықтама.y=f(x) функция графигі (а,в) интервалының кез келген нүктесінде жүргізілген жанамадан төмен жатса, онда функция дөңес (дөңестігі жоғары қараған) деп, ал жанамадан жоғары жатса, онда функция ойыс (дөңестігі төмен қараған) деп аталады.
3-суретте y=f(x) функциясының графигі 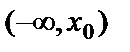 аралығында дөңес болады да, ал
аралығында дөңес болады да, ал 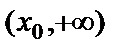 аралығында ойыс болады.Функция дөңестігінің жеткілікті шарты. (а,в) интервалында y=f(x) функциясының екінші ретті туындысы теріс таңбалы болса, функция графигі осы аралықта дөңес, ал екінші туындысы оң таңбалы болса, функция графигі осы аралықта ойыс болады.
аралығында ойыс болады.Функция дөңестігінің жеткілікті шарты. (а,в) интервалында y=f(x) функциясының екінші ретті туындысы теріс таңбалы болса, функция графигі осы аралықта дөңес, ал екінші туындысы оң таңбалы болса, функция графигі осы аралықта ойыс болады.
Б)Иілу нүктесі.Анықтама.Функция графигінің дөңес және ойыс бөліктерін бөліп тұратын нүктені функцияның иілу нүктесі деп атайды. Суретте қисық бойында жатқан (x0, f(x0)) нүкте графиктің дөңес және ойыс бөліктерін бөліп тұр, яғни ол функцияның иілу нүктесі болады. Иілу нүктесі бар болуының жеткілікті шарты. (а,в) интервалында екі рет дифференциалданатын y=f(x) функциясының екінші туындысы х аргумент х0 нүкте арқылы өткенде таңбасын өзгертсе, онда (x0, f(x0)) нүктесі функцияның иілу нүктесі болады.
Мысал. 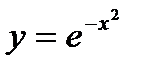 (Гаусс қисығы) функциясының иілу нүктелері мен дөңестік аралықтарын тап.Шешуі. 1) Функция бүкіл сан осінде анықталған, яғни D(y)=
(Гаусс қисығы) функциясының иілу нүктелері мен дөңестік аралықтарын тап.Шешуі. 1) Функция бүкіл сан осінде анықталған, яғни D(y)= 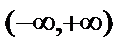 .
.
2) Бірінші және екінші туындыларын табамыз: 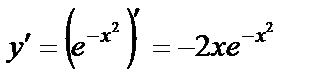 ;
;
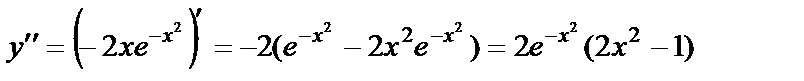 .
.
3)ІІ-текті күдікті нүктелерін 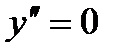 шартынан табамыз:
шартынан табамыз: 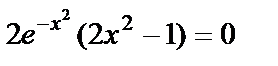 .
. 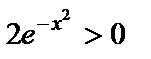 болғандықтан,
болғандықтан, 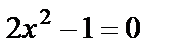 . Осыдан
. Осыдан 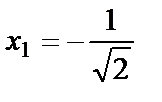 және
және 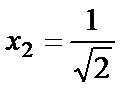 күдікті нүктелер табылады. Осы нүктелер анықталу облысын үш интервалға бөледі:
күдікті нүктелер табылады. Осы нүктелер анықталу облысын үш интервалға бөледі:
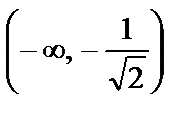 ,
, 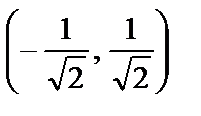 ,
, 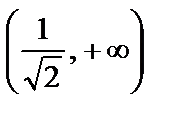 .
.
Осы интервалдардағы екінші туынды таңбасын анықтаймыз (4-сурет):
у 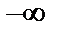 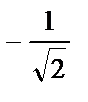 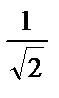 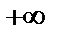 Ойыс дөңес ойыс |
Сонымен,функция графигі 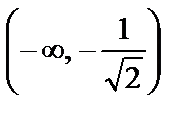 және
және 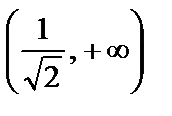 аралықтарда ойыс, ал
аралықтарда ойыс, ал 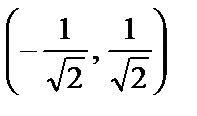 аралықта дөңес болады екен. Екінші ретті
аралықта дөңес болады екен. Екінші ретті 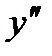 туынды
туынды 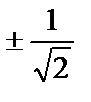 нүктелерден өткенде таңбасын өзгертетіндіктен, бұл нүктелер функцияның иілу нүктелері болады
нүктелерден өткенде таңбасын өзгертетіндіктен, бұл нүктелер функцияның иілу нүктелері болады
С)АСИМПТОТАЛАРЫ.Анықтама.Егер y=f(x) функциясы үшін 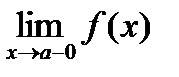 және
және 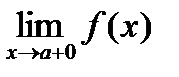 шектерінің ең болмағанда біреуі шексіздікке тең болса, онда
шектерінің ең болмағанда біреуі шексіздікке тең болса, онда 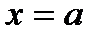 функция графигінің тік асимптотасы деп аталады (6а-сурет).
функция графигінің тік асимптотасы деп аталады (6а-сурет).
у=kx+b түзуі y=f(x) функция графигінің көлбеу асимптотасы деп аталады, егер функцияға тиісті қандай да бір М нүкте координат басынан алыстаған сайын түзуге шексіз жақындаса (6б-сурет).
у у
6а-сурет 6б-сурет |
Көлбеу асимптотаның дербес жағдайы (k=0) горизонталь асимптота болады: y=b
Көлбеу асимптотаны мынадай теорема көмегімен табуға болады.
Теорема. у=kx+b түзуі y=f(x) функция графигінің көлбеу асимптотасы болуы үшін мынадай шектердің бар болуы қажетті және жеткілікті: 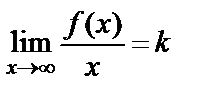 ,
, 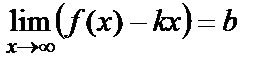 .
.

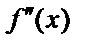 + - +
+ - +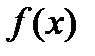 х
х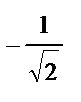 0
0