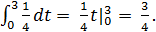Дисперсия дискретных случайных величин
Определение. Дисперсией случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
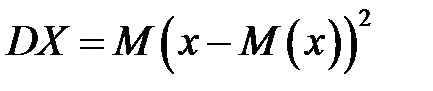= D(X) = M( 
Величина x – M(X) называется отклонением случайной величины от ее математического ожидания.
Свойства дисперсии
1. Дисперсия постоянной величины С равна нулю.
2. Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат
D(CX) = 
.
3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин
D(X+Y) = D(X) + D(Y).
4. Дисперсия разности двух независимых случайных величин равна
сумме дисперсий этих величин
D(X-Y) = D(X) + D(Y).
Пример.
Дисперсия случайной величины Х равна 3. Найти дисперсию следующих величин: а) -3Х, б) 4Х + 3.
Средним квадратическим отклонением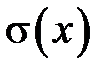 
случайной величины 
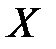называется корень квадратный из ее дисперсии:
, 
.
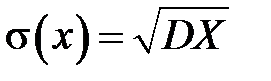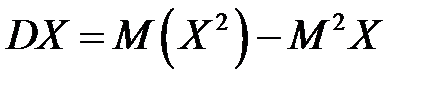Пример 1.
Случайная величина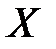 
– число очков, выпавших при однократном бросании игральной кости. Определить 
.
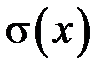Решение.
 | ||||||
 |  | | | | | |
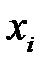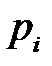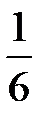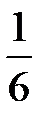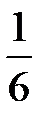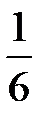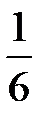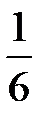Имеем
;
.
.
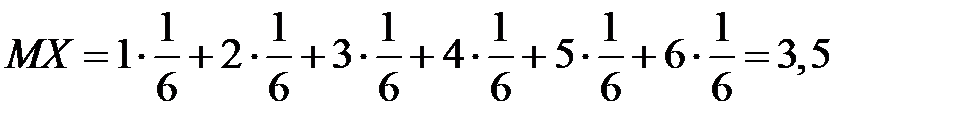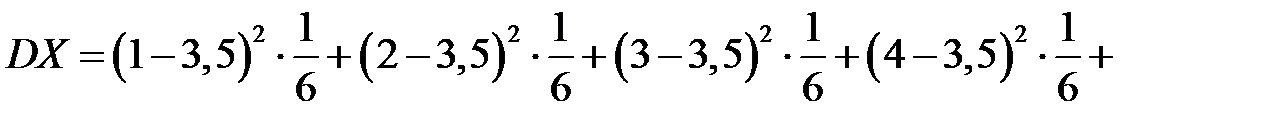
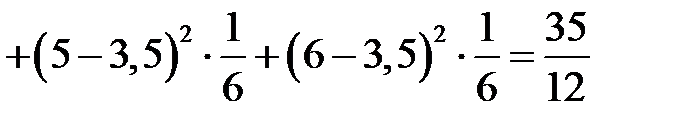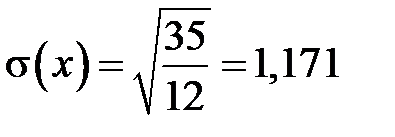Непрерывные случайные величины
Для непрерывной случайной величины, в отличие от дискретной, нельзя построить ряд распределения. Поэтому непрерывную случайную величину изучают другим способом.
Пусть Х - непрерывная случайная величина с возможными значениями из (а,в). Тогда для нее существует функция распределения
F(х) = P(х<x).
Свойства функции распределения:
1. 0 ≤ F(х) ≤ 1;
2. F(х) - неубывающая функция;
3. P(a ≤ x <в) = F(a) – F(в);
4. Вероятность того, что непрерывная случайная величина Х примет какое-либо заранее заданное значение, рана нулю.
5. Вероятности попадания непрерывной случайной величины в интервал, сегмент, полуинтервал с одними и теми же концами одинаковы
P(a ≤ x <b) = P(a < x ≤ b) = P(a ≤ x ≤ b) =P(a < x ≤ b).
6. Если возможные значения случайной величины Х принадлежат интервалу (а,d) , то
1. F(х) = 0 при х ≤ a;
2. F(х) =1 при х ≤ d;
3.
Дифференциальная функция распределения (плотность распределения).
Определение. Плотностью распределения f(x) (или дифференциальной функцией распределения) непрерывной случайной величины называется
первая производная от ее функция распределения
.
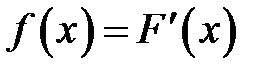Свойства плотности распределения:
1)f(x)≥ 0;
2)f(-∞ )= f(-∞) = 0;
3)f(x) – кусочно непрерывная функция;
4)F(х) =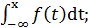 
5)P(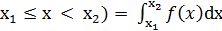 
;
6) 
.
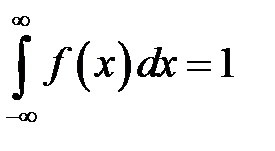Вероятность попадания случайной величины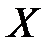 
на участок от 
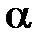до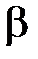 
выражается формулой
,
.
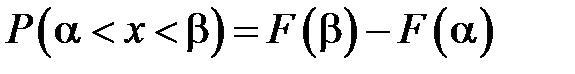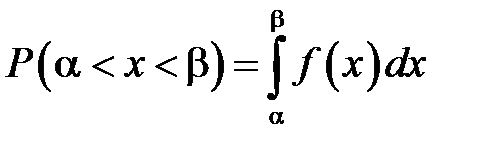Пример 1.
Возможно ли, что принекотором значении аргумента:
1. Функция распределения больше 1?
2. Плотность распределения больше 1?
3. Функция распределения отрицательной?
4. Плотность распределения отрицательной?
Пример.
Задана плотность распределения непрерывной случайной величины:
f(x) =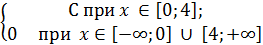 
Найти константу С и (0 вычислить Р < х < 3).
Решение.
На основании свойств плотности распределения имеем:
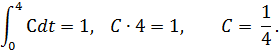
Таким образом
f(x) =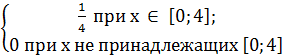 
На основании свойства 5 имеем
Р < х < 3) = 