Переходный, принужденный и свободный режимы электрической цепи

Возникновение переходных процессов в электрических цепях

Переходный процесс – это переход от одного установившегося режима к другому. Например различного рода коммутации (переключения), которые приводят к изменению состояния электрической цепи (подключаются или отключаются источники питания, изменяется конфигурация цепи и ее параметры).

Переходный процесс не может происходить мгновенно. Как правило токи и напряжения изменяются монотонно либо колебательно (рис.1).

Задача расчета переходных процессов – установить законы изменения токов и напряжений цепи в зависимости от времени и дать им анализ.

Изучение переходных процессов представляет большой практический интерес. Значения токов и напряжений на отдельных участках цепи могут существенно превышать значения в установившихся режимах, что в ряде случаев приводит к нарушениям нормальной работы оборудования и даже аварийным ситуациям. Знание характера протекания переходных процессов позволяет еще на этапе проектирования предусмотреть меры, предупреждающие пробой изоляции или механическое повреждение электроустановок. Анализ переходных процессов целесообразно проводить во многих радиотехнических и импульсных устройствах, устройствах автоматики и компьютерной техники.

Переходный, принужденный и свободный режимы электрической цепи

Рассмотрим подключение неразветвленной цепи R, L, C к источнику напряжения (рис.2)

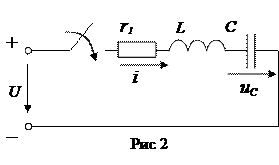
После замыкания ключа в цепи будет протекать ток переходного процесса, который создает падения напряжения на элементах.

Запишем второй закон Кирхгофа для мгновенных значений

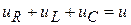. (1)

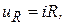
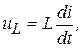
С учетом функциональных зависимостей 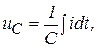переходный режим описывается интегро-дифференциальным уравнением

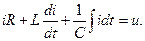(2)

Через определенный промежуток времени в цепи наступит установившийся или принужденный режим и уравнение (2) примет следующий вид

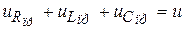, или

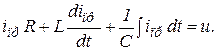(3)

Принужденные токи и напряжения рассчитываются в установившемся режиме цепи любыми ранее изученными методами.

Разница между переходным и принужденным режимами характеризуется свободным режимом параметры которого соответственно равны

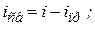
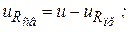
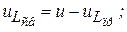
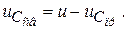
В свободном режиме параметры цепи не зависят от внешних сил. Тогда приравняв нулю правую часть уравнения (2) запишем

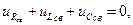
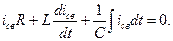(4)

Уравнение (4) является линейным однородным интегро-дифференциальным уравнением с постоянными коэффициентами, решение которого в общем виде представляют как

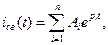
где р_i – корн характеристического уравнения. Порядок уравнения как правило равен числу реактивных элементов (исключения составляют индуктивные сечения и емкостные контуры).

А_i – постоянные интегрирования, которые определяются из начальных условий.