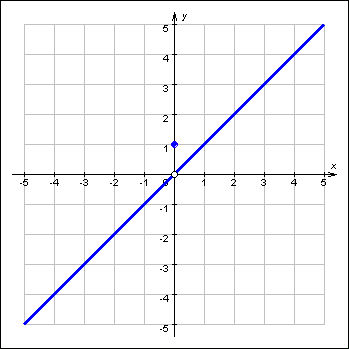
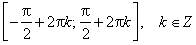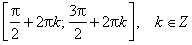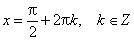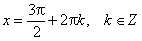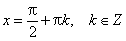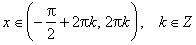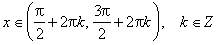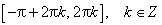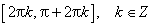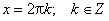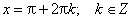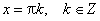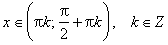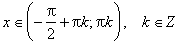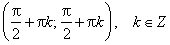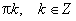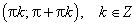Четность, нечетность, периодичность тригонометрических функций
Известно, что для любого значение x верны равенства
sin (-x) = -sin x, cos (-x) = cos x
Следовательно, y = sin x — нечетная функция, а y = cos x — чётная функция. Так как для любого значения x из области определения функции y = tg x верно равенство tg (-x) = -tg x, тоy = tg x — нечетная функция.
Известно, что для любого значения x верны равенства
sin (x + 2π) = sin x, cos (x + 2π) = cos x.
Из этих равенств следует, что значения синуса и косинуса периодически повторяются при изменении аргумента на 2π. Такие функции называются периодическими с периодом 2π.
Функция f (x) называется периодической, если существует такое число T ≠ 0, что для любого xиз области определения этой функции выполняется равенство f (x - T) = f (x) = f (x + T).
Число T называется периодом функции f (x).
Из этого определения следует, что если x принадлежит области определения функции f (x), то числа x + T, x - T и вообще числа x + Tn, n Є Z, также принадлежат области определения этой периодической функции и f (x + Tn) = f (x), n Є Z
Число 2π является наименьшим положительным периодом функции y = cos x, также и для функции y = sin x.
π - наименьший положительный период функции tg x.
Функция синус
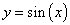
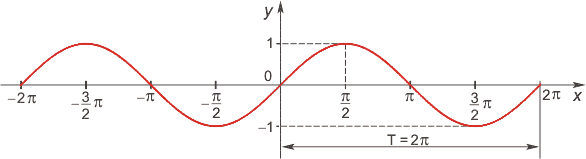 | ||||||||
Область определения функции— множество Rвсех действительных чисел. Множество значений функции — отрезок [-1; 1], т.е. синус функция — ограниченная. Функция нечетная: sin(−x)=−sin x для всех х ∈ R. График функции симметричен относительно начала координат. Функция периодическая с наименьшим положительным периодом 2π: sin(x+2π·k) = sin x, где k ∈ Z для всех х ∈ R. sin x = 0 при x = π·k, k ∈ Z. sin x > 0 (положительная) для всех x ∈ (2π·k, π+2π·k), k ∈ Z. sin x < 0 (отрицательная) для всех x ∈ (π+2π·k, 2π+2π·k), k ∈ Z.
|
Функция косинус
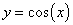
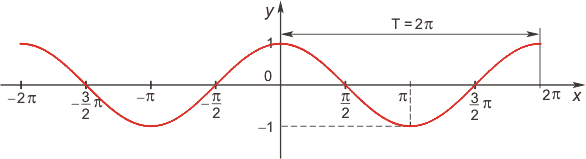 | ||||||||||||||
Область определения функции— множество Rвсех действительных чисел. Множество значений функции — отрезок [-1; 1], т.е. косинус функция — ограниченная. Функция четная: cos(−x)=cos x для всех х ∈ R. График функции симметричен относительно оси OY. Функция периодическая с наименьшим положительным периодом 2π: cos(x+2π·k) = cos x, где k ∈ Z для всех х ∈ R.
|
Функция тангенс
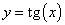
 | ||||||||||
Множество значений функции — вся числовая прямая, т.е. тангенс — функция неограниченная. Функция нечетная: tg(−x)=−tg x для всех х из области определения. Функция периодическая с наименьшим положительным периодом π, т.е. tg(x+π·k) = tg x, k ∈ Z для всех х из области определения.
|
Функция котангенс
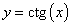
 | ||||||||||
Множество значений функции — вся числовая прямая, т.е. котангенс — функция неограниченная. Функция нечетная: ctg(−x)=−ctg x для всех х из области определения. Функция периодическая с наименьшим положительным периодом π, т.е. ctg(x+π·k)=ctg x, k ∈ Z для всех х из области определения.
|
Предел функции
Понятие предела функции является одним из самых важных в математике. Дадим два определения этому понятию.
Определение предела по Коши. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для каждого ε > 0 существует δ > 0 такое, что для всех x, удовлетворяющих условию |x – a| < δ, x ≠ a, выполняется неравенство |f (x) – A| < ε.
Определение предела по Гейне. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для любой последовательности 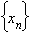 такой, что
такой, что 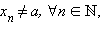 сходящейся к числу a, соответствующая последовательность значений функции
сходящейся к числу a, соответствующая последовательность значений функции 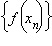 сходится к числу A.
сходится к числу A.
| |
| График 1.3.6.1. Предел функции y = x2 при x → 2. |
| |
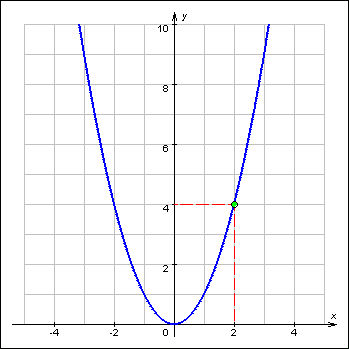
График 1.3.6.2. Предел функции 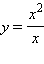 при x → 0. при x → 0. |
Если A – предел функции в точке a, то пишут, что
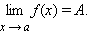 |
Определения предела функции по Коши и по Гейне эквивалентны.
| |
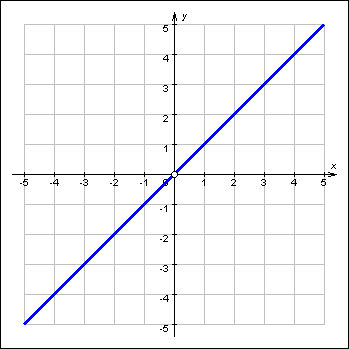
| График 1.3.6.3. Предел функции y = {x (x ≠ 0); 1 (x = 0)} приx → 0 равен 0. |
Предел функции 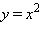 в точке a = 0 равен 0:
в точке a = 0 равен 0: 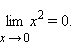 Предел функции
Предел функции 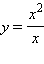 в точке a = 0 также равен 0, хотя эта функция не существует в этой точке (ее знаменатель обращается в нуль). Предел функции
в точке a = 0 также равен 0, хотя эта функция не существует в этой точке (ее знаменатель обращается в нуль). Предел функции  в точке a = 0 равен 0, хотя значение функции в этой точке f (0) = 1.
в точке a = 0 равен 0, хотя значение функции в этой точке f (0) = 1.
Если функция f (x) имеет предел в точке a, то этот предел единственный.
Число A1 называется пределом функции f (x) слева в точке a, если для каждого ε > 0 существует δ > 0 такое, что для всех 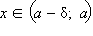 выполняется неравенство
выполняется неравенство 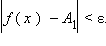
Число A2 называется пределом функции f (x) справа в точке a, если для каждого ε > 0 существует δ > 0 такое, что для всех 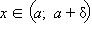 выполняется неравенство
выполняется неравенство 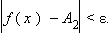
Предел слева обозначается 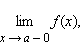 предел справа –
предел справа – 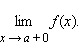 Эти пределы характеризуют поведение функции слева и справа от точки a. Их часто называют односторонними пределами. В обозначении односторонних пределов при x → 0обычно опускают первый нуль:
Эти пределы характеризуют поведение функции слева и справа от точки a. Их часто называют односторонними пределами. В обозначении односторонних пределов при x → 0обычно опускают первый нуль:  и
и 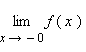 . Так, для функции
. Так, для функции 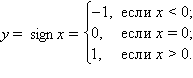
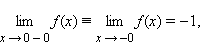
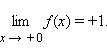
Если для каждого ε > 0 существует такая δ-окрестность точки a, что для всех x, удовлетворяющих условию |x – a| < δ, x ≠ a, выполняется неравенство |f (x)| > ε, то говорят, что функция f (x) имеет в точке a бесконечный предел:
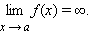 |
Так, функция 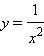 имеет в точке x = 0 бесконечный предел
имеет в точке x = 0 бесконечный предел 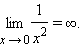 Часто различают пределы, равные +∞ и –∞. Так,
Часто различают пределы, равные +∞ и –∞. Так, 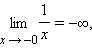
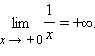
Если для каждого ε > 0 существует такое δ > 0, что для любого x > δ выполняется неравенство |f (x) – A| < ε, то говорят, что предел функции f (x) при x, стремящемся к плюс бесконечности, равен A:
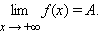 |
Аналогично формулируется определение предела при x, стремящемся к минус бесконечности: 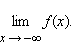 В качестве примера приведем функцию
В качестве примера приведем функцию 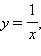 которая стремится на бесконечности к нулю:
которая стремится на бесконечности к нулю: 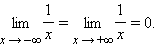
Наконец, запись 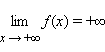 означает, что для любого ε > 0 существует такое δ > 0, что для любого x > δ выполняется неравенство f (x) > ε. Запись
означает, что для любого ε > 0 существует такое δ > 0, что для любого x > δ выполняется неравенство f (x) > ε. Запись 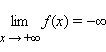 означает, что для любого ε > 0 существует такое δ > 0, что для любого x > δ выполняется неравенство f (x) < –ε. Запись
означает, что для любого ε > 0 существует такое δ > 0, что для любого x > δ выполняется неравенство f (x) < –ε. Запись 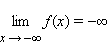 означает, что для любого ε > 0 существует такое δ > 0, что для любого x < –δ выполняется неравенство f (x) < –ε.
означает, что для любого ε > 0 существует такое δ > 0, что для любого x < –δ выполняется неравенство f (x) < –ε.
Если функция f (x) имеет конечный предел в точке a, то существует окрестность точки a, в которой функция f ограничена ( возможно, что в самой точке a функция не определена). При этом, если A ≠ 0, то найдется окрестность точки a, в которой (быть может, за исключением самой точки a) значения функции f имеют тот же знак, что и число A.
Если существует такое δ > 0, что для всех x, принадлежащих δ-окрестности точки a, выполняются неравенства
| g (x) ≤ f (x) ≤ h (x), |
и если
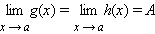 , , |
то существует 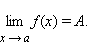
Если существует такое δ > 0, что для всех x, принадлежащих δ-окрестности точки a, справедливо неравенство
| f (x) < g (x), |
и если 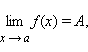
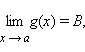 то A ≤ B.
то A ≤ B.