Векторы угловой скорости и углового ускорения
Введем понятия векторов угловой скорости и углового ускорения тела. Если 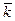 – единичный вектор оси вращения, направленный в ее положительную сторону, то векторы угловой скорости
– единичный вектор оси вращения, направленный в ее положительную сторону, то векторы угловой скорости 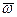 и углового ускорения
и углового ускорения 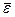 определяют выражениями:
определяют выражениями:
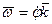 ,
, 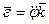 . (73)
. (73)
Так как 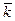 – постоянный по модулю и направлению вектор, то из (63) следует, что
– постоянный по модулю и направлению вектор, то из (63) следует, что
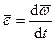 . (74)
. (74)



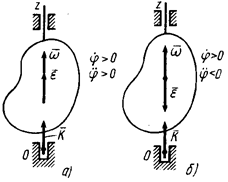 При
При 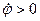 и
и  направления векторов
направления векторов  и
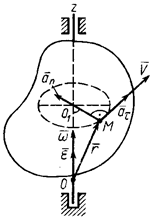
и 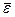 совпадают. Они оба направлены в положительную сторону оси вращения Оz (рис. 31, а). Если
совпадают. Они оба направлены в положительную сторону оси вращения Оz (рис. 31, а). Если 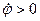 и
и 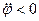 , то они направлены в противоположные стороны (рис. 32, б). Вектор углового ускорения совпадает по направлению с вектором угловой скорости при ускоренном вращении и противоположен ему при замедленном. Векторы
, то они направлены в противоположные стороны (рис. 32, б). Вектор углового ускорения совпадает по направлению с вектором угловой скорости при ускоренном вращении и противоположен ему при замедленном. Векторы 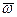 и
и 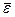 можно изображать в любых точках оси вращения.
можно изображать в любых точках оси вращения.
Векторные формулы для скоростей и ускорений точек тела
Выразим скорость, касательное, нормальное и полное ускорения точки тела в векторной форме (рис. 32). Скорость точки по модулю и направлению можно представить векторным произведением
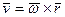 , (75)
, (75)
 где
где 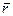 – радиус-вектор точки
– радиус-вектор точки  , проведенный из произвольной точки оси вращения
, проведенный из произвольной точки оси вращения 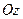 , например точки
, например точки 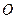 . Выражение (75) называется векторной формулой Эйлера.
. Выражение (75) называется векторной формулой Эйлера.
Из определения ускорения и векторной формулы Эйлера имеем:
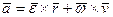 . (76)
. (76)
Первое слагаемое в (76) является касательным ускорением, а второе – нормальным, т. е.
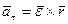 ,
, 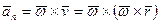 . (77)
. (77)
Сложное движение точки
Для изучения некоторых, более сложных видов движений твердого тела целесообразно рассмотреть простейшее сложное движение точки. Во многих задачах движение точки приходится рассматривать относительно двух (и более) систем отсчета, движущихся друг относительно друга. Так, движение космического корабля, движущегося к Луне, требуется рассматривать одновременно и относительно Земли и относительно Луны, которая движется относительно Земли. Любое движение точки можно считать сложным, состоящим из нескольких движений.
В простейшем случае сложное движение точки состоит из относительного и переносного движений. Определим эти движения. Пусть имеем две системы отсчета, движущиеся друг относительно друга. Если одну из этих систем 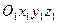 (рис. 33) принять за основную или неподвижную (ее движение относительно других систем отсчета не рассматривается), то вторая система отсчета
(рис. 33) принять за основную или неподвижную (ее движение относительно других систем отсчета не рассматривается), то вторая система отсчета 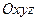 будет двигаться относительно первой. Движение точки относительно подвижной системы отсчета
будет двигаться относительно первой. Движение точки относительно подвижной системы отсчета 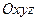 называется относительным. Характеристики этого движения, такие, как траектория, скорость и ускорение, называются относительными. Их обозначают индексом
называется относительным. Характеристики этого движения, такие, как траектория, скорость и ускорение, называются относительными. Их обозначают индексом 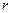 ; для скорости и ускорения
; для скорости и ускорения 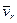 и
и 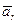 . Движение точки относительно основной, или неподвижной, системы отсчета
. Движение точки относительно основной, или неподвижной, системы отсчета 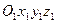 называется абсолютным (или сложным). Его также иногда называют составным движением. Траектория, скорость и ускорение этого движения называются абсолютными. Скорость и ускорение абсолютного движения обозначают буквами
называется абсолютным (или сложным). Его также иногда называют составным движением. Траектория, скорость и ускорение этого движения называются абсолютными. Скорость и ускорение абсолютного движения обозначают буквами 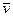 и
и 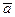 без индексов. Переносным движением называют движение подвижной системы отсчета по отношению к неподвижной. Вследствие относительного движения движущаяся точка в различные моменты времени совпадает с различными точками тела
без индексов. Переносным движением называют движение подвижной системы отсчета по отношению к неподвижной. Вследствие относительного движения движущаяся точка в различные моменты времени совпадает с различными точками тела 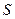 , с которым скреплена подвижная система отсчета. Переносной скоростью и переносным ускорением являются скорость и ускорение той точки тела
, с которым скреплена подвижная система отсчета. Переносной скоростью и переносным ускорением являются скорость и ускорение той точки тела 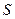 , с которой в данный момент совпадает движущаяся точка. Переносные скорость и ускорение обозначают
, с которой в данный момент совпадает движущаяся точка. Переносные скорость и ускорение обозначают 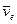 и
и 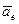 .
.
Теорема сложения скоростей: скорость абсолютного движения точки равна векторной сумме скоростей переносного и относительного движений этой точки
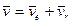 . (78)
. (78)
Так как в общем случае скорости переносного и относительного движений не перпендикулярны, то
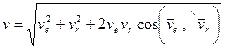 .
.
Абсолютную скорость можно представить в виде:
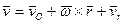 . (79)
. (79)
Скорость
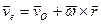
является скоростью точки свободного твердого тела, скрепленного с подвижной системой координат, с которой в данный момент совпадает точка  в движении тела относительно неподвижной системы осей координат. Это есть переносная скорость точки
в движении тела относительно неподвижной системы осей координат. Это есть переносная скорость точки  .
.
Теорема сложения ускорений точки (кинематическая теорема Кориолиса): абсолютное ускорение точки является векторной суммой трех ускорений – переносного, относительного и Кориолиса
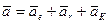 , (80)
, (80)
где
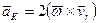 . (81)
. (81)
Ускорение 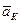 называется ускорением Кориолиса. Иногда его также называют добавочным (или поворотным) ускорением.
называется ускорением Кориолиса. Иногда его также называют добавочным (или поворотным) ускорением.
Абсолютное ускорение можно также представить в виде:
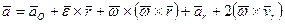 . (82)
. (82)
В этой формуле первые три слагаемых составляют ускорение точки свободного твердого тела в общем случае его движения вместе с подвижной системой осей координат относительно неподвижной. Первое слагаемое 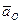 – ускорение точки
– ускорение точки 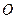 ,
, 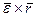 и
и 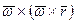 – соответственно вращательное и нормальное ускорения точки
– соответственно вращательное и нормальное ускорения точки  , если бы она двигалась только вместе с подвижной системой осей координат, не имея в рассматриваемый момент времени относительного движения.
, если бы она двигалась только вместе с подвижной системой осей координат, не имея в рассматриваемый момент времени относительного движения.
При координатном способе задания в декартовых координатах
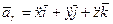 ,
,
где 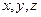 – координаты движущейся точки относительно подвижной системы осей координат;
– координаты движущейся точки относительно подвижной системы осей координат; 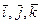 – единичные векторы этих осей. При естественном способе задания движения
– единичные векторы этих осей. При естественном способе задания движения
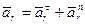 ,
, 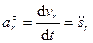 ,
, 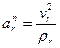 ,
,
где 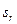 – расстояние от начала отсчета до точки по траектории относительного движения;
– расстояние от начала отсчета до точки по траектории относительного движения; 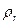 – радиус кривизны этой траектории. В частном случае, когда переносное движение есть вращение вокруг неподвижной оси, переносное ускорение
– радиус кривизны этой траектории. В частном случае, когда переносное движение есть вращение вокруг неподвижной оси, переносное ускорение
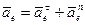 ,
,
где касательное переносное ускорение
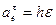 ,
,
причем 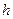 – кратчайшее расстояние от движущейся точки до оси вращения. Нормальное переносное ускорение
– кратчайшее расстояние от движущейся точки до оси вращения. Нормальное переносное ускорение
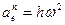 .
.
Абсолютное ускорение в этом случае
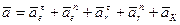 . (83)
. (83)
Ускорение Кориолиса
Рассмотрим ускорение Кориолиса и его свойства. Оно определяется формулой (81)
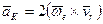 .
.
Угловую скорость вращательной части движения подвижной системы отсчета, т.е. угловую скорость переносного движения, обозначили как 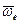 .
.
Ускорение Кориолиса является результатом взаимного влияния двух движений: переносного и относительного. Часть его 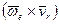 получается вследствие изменения переносной скорости точки из-за относительного движения. Другая его часть, тоже
получается вследствие изменения переносной скорости точки из-за относительного движения. Другая его часть, тоже 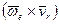 , есть результат изменения относительной скорости вследствие переносного движения.
, есть результат изменения относительной скорости вследствие переносного движения.
Модуль ускорения Кориолиса в соответствии с (81) определяется выражением
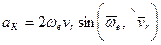 . (84)
. (84)
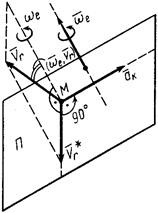
Для определения ускорения Кориолиса очень удобно правило Жуковского Н. Е. Оно основано на формуле (81). Пусть имеем точку  , движущуюся с относительной скоростью
, движущуюся с относительной скоростью 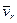 , (рис. 34). Построим плоскость
, (рис. 34). Построим плоскость 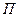 , перпендикулярную угловой скорости переносного вращения
, перпендикулярную угловой скорости переносного вращения 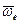 , и спроецируем
, и спроецируем 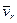 на эту плоскость. Проекцию обозначим
на эту плоскость. Проекцию обозначим 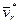 . Она является вектором; ее модуль
. Она является вектором; ее модуль
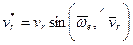 .
.
 Ускорение Кориолиса выразится в форме
Ускорение Кориолиса выразится в форме
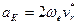 . (84')
. (84')
Учитывая (81) и (84'), получаем правило Жуковского: модуль ускорения Кориолиса равен удвоенному произведению угловой скорости переносного вращения на модуль проекции относительной скорости на плоскость, перпендикулярную оси переносного вращения; чтобы получить направление ускорения Кориолиса, следует вектор проекции относительной скорости 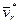 повернуть на 90° вокруг оси, параллельной оси переносного вращения, в направлении этого вращения.
повернуть на 90° вокруг оси, параллельной оси переносного вращения, в направлении этого вращения.
Рассмотрим случаи обращения в нуль ускорения Кориолиса. Из (84) следует, что 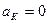 , если:
, если:
1) 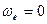 , т.е. переносное движение является поступательным;
, т.е. переносное движение является поступательным;
2) 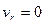 , т.е. в те моменты времени, в которые происходит изменение направления относительного движения;
, т.е. в те моменты времени, в которые происходит изменение направления относительного движения;
3) 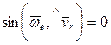 , т.е. когда скорость относительного движения
, т.е. когда скорость относительного движения 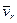 параллельна угловой скорости переносного вращения
параллельна угловой скорости переносного вращения 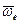 .
.
