Дифференциальные уравнения движения точки

С помощью дифференциальных уравнений движения решается вторая задача динамики. Правила составления таких уравнений зависят от того, каким способом хотим определить движение точки.

1) Определение движения точки координатным способом.

Рассмотрим свободную материальную точку, движущуюся под действием сил 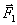, ,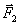.., . 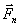Проведем неподвижные координатные оси Oxyz (рис.4). Про­ектируя обе части равенства 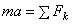на эти оси и учитывая, что 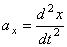и т.д., получим дифферен­циальные уравнения криволинейного дви­жения точки в проекциях на оси прямо­угольной декартовой системы координат:

, , .

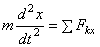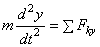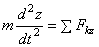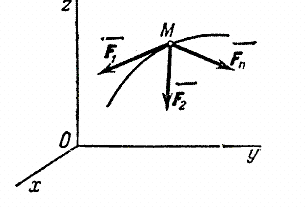
Рис.4

Так как действующие на точку силы мо­гут зависеть от времени, от положения точки и от ее скорости, то правые части уравнений могут содержать время t, координаты точки х, у, z и проекции ее скорости 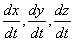. При этом в правую часть каждого из уравнений могут входить все эти переменные.

Чтобы с помощью этих уравнений решить основную задачу динамики, надо, кроме действующих сил, знать еще начальные условия, т.е. положение и скорость точки в начальный момент. В координатных осях Oxyz начальные условия задаются в виде: при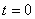

.

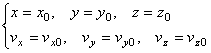Зная действующие силы, после интегрирования уравнений найдем координаты х, y, z движущейся точки, как функции времени t, т.е. найдем закон движения точки.

Пример 3. Изучим движение тела, брошенного с начальной скоростью 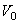под углом 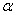к горизонту, рассматривая его как материальную точку массы т. При этом сопротивлением воздуха пренебрежём, а поле тяжести будем считать однородным (Р=const), полагая, что дальность полёта и высота траектории малы по сравнению с радиусом Земли.

Поместим начало координат О в начальном положении точки. Направим ось 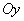вертикально вверх; горизонтальную ось Ox расположим в плоскости, проходящей через Оy и вектор 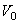, а ось Oz проведём перпендикулярно первым двум осям (рис.5). Тогда угол между вектором 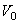и осью Ox будет равен .

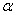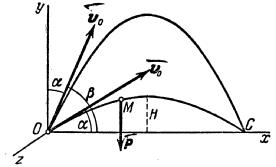
Рис.5

Изобразим движущуюся точку М где-нибудь на траектории. На точку действует одна только сила тяжести 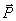, проекции которой на оси координат равны: , , .

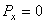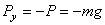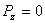Подставляя эти величины в дифференциальные уравнения и замечая, что 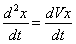и т.д. мы после сокращения на m получим:

, , .

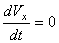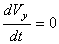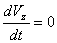Умножая обе части этих уравнений на dt и интегрируя, находим:

, ,

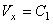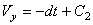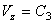
Начальные условия в нашей задаче имеют вид:

при t=0:

,

,

, .

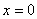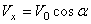
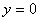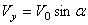
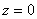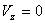Удовлетворяя начальным условиям, будем иметь:

, , .

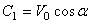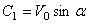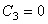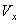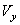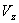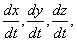Подставляя эти значения С₁, С₂ и С₃ в найденное выше решение и заменяя , , на придём к уравнениям:

.

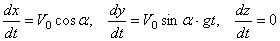Интегрируя эти уравнения, получим:

.

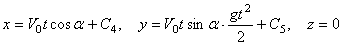Подстановка начальных данных даёт С₄=С₅=С₆=0, и мы окончательно находим уравнения движения точки М в виде:

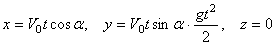(1)

Из последнего уравнения следует, что движение происходит в плоскости Оxy.

Имея уравнение движения точки, можно методами кинематики определить все характеристики данного движения.

1. Траектория точки. Исключаяиз первых двух уравнений (1) время t, получим уравнение траектории точки:

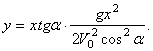(2)

Это - уравнение параболы с осью, параллельной оси Оy. Таким образом, брошенная под углом к горизонту тяжёлая точка движется в безвоздушном пространстве по параболе (Галилей).

2. Горизонтальная дальность. Определим горизонтальную дальность, т.е. измеренное вдоль оси Оx расстояние ОС=Х. Полагая в равенстве (2) y=0, найдём точки пересечения траектории с осью Ох. Из уравнения:

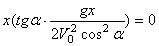
получаем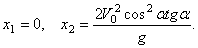

Первое решение дает точку О, второе точку С. Следовательно, Х=Х₂ и окончательно

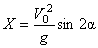. (3)

Из формулы (3) видно, что такая же горизонтальная дальность Xбудет получена при угле 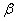, для которого 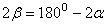, т.е. если угол 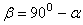. Следовательно, при данной начальной скорости 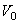в одну и ту же точку С можно попасть двумя траекториями: на­стильной ( 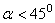) и навесной ( ).

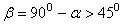При заданной начальной скорости 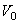наибольшая горизонтальная дальность в безвоздушном пространстве получается, когда 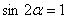, т.е. при угле .

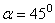3. Высота траектории. Если положить в уравнении (2)

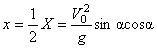, то найдется высота траектории Н:

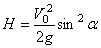. (4)

4. Время полета. Из первого уравнения системы (1) следует, что полное время полета Т определяется равенством 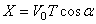. Заменяя здесь Х его значением, получим

.

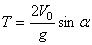При угле наибольшей дальности 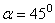все найденные вели­чины равны:

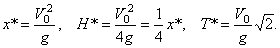
Полученные результаты практически вполне приложимы для ориен­тировочного определения характеристик полета снарядов (ракет), имеющих дальности порядка 200…600 км, так как при этих дальностях (и при 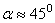) снаряд основную часть своего пути проходит в стратосфере, где сопротивлением воздуха можно пренебречь. При меньших дальностях на результат будет сильно влиять сопротивле­ние воздуха, а при дальностях свыше 600 км силу тяжести уже нельзя считать постоянной.

Пример 4. Из пушки, установленной на высоте h, произвели выстрел под углом 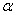к горизонту (рис. 6). Ядро вылетело из ствола орудия со скоростью u. Определим уравнения движения ядра.

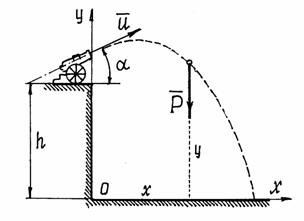
Рис.6

Чтобы правильно составить дифференциальные уравнения движения, надо решать подобные задачи по определённой схеме.

а) Назначить систему координат (количество осей, их направление и начало координат). Удачно выбранные оси упрощают решение.

б) Показать точку в промежуточном положении. При этом надо проследить за тем, чтобы координаты такого положения обязательно были положительными (рис.6).

в) Показать силы, действующие на точку в этом промежуточном положении (силы инерции не показывать!).

В этом примере – это только сила 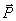, вес ядра. Сопротивление воздуха учитывать не будем.

г) Составить дифференциальные уравнения по формулам: 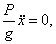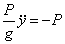. Отсюда получим два уравнения: 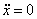и .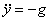

д) Решить дифференциальные уравнения.

Полученные здесь уравнения – линейные уравнения второго порядка, в правой части – постоянные. Решение этих уравнений элементарно.

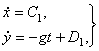и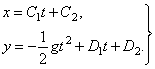

Осталось найти постоянные интегрирования. Подставляем начальные условия (при t = 0 x = 0, y = h, 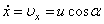, 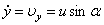) в эти четыре уравнения: 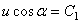, , 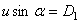0 = С₂, h = D₂.

Подставляем в уравнения значения постоянных и записываем уравнения движения точки в окончательном виде

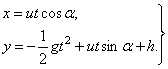
Имея эти уравнения, как известно из раздела кинематики, можно определить и траекторию движения ядра, и скорость, и ускорение, и положение ядра в любой момент времени.

Как видно из этого примера, схема решения задач довольно проста. Сложности могут возникнуть только при решении дифференциальных уравнений, которые могут оказаться непростыми.

2) Определение движения точки естественным способом.

Координатным способом обычно определяют движение точки, не ограниченные какими-либо условиями, связями. Если на движение точки наложены ограничения, на скорость или координаты, то определить такое движение координатным способом совсем не просто. Удобнее использовать естественный способ задания движения.

Определим, например, движение точки по заданной неподвижной линии, по заданной траектории (рис. 7).

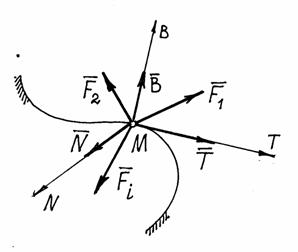
Рис.7

На точку М кроме заданных активных сил 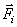, действует реакция линии. Показываем составляющие реакции 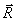по естественным осям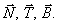

Составим основное уравнение динамики 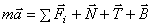и спроектируем его на естественные оси

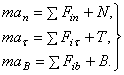
Так как 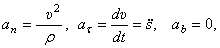то получим дифференциальные уравнения движения, такие

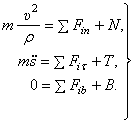(5)

Здесь сила 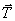- сила трения. Если линия, по которой движется точка, гладкая, то Т = 0 и тогда второе уравнение будет содержать только одну неизвестную – координату s:

.

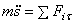Решив это уравнение, получим закон движения точки 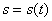, а значит, при необходимости, и скорость и ускорение. Первое и третье уравнения (5) позволят найти реакции 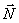и .

Рис. 13.5.

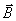Пример 5. Лыжник спускается по цилиндрической поверхности радиуса r. Определим его движение, пренебрегая сопротивлениями движению (рис. 8).

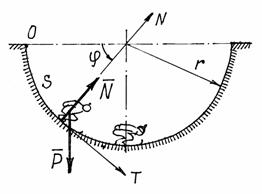
Рис.8

Схема решения задачи та же, что и при координатном способе (пример 4). Отличие лишь в выборе осей. Здесь оси N и Т движутся вместе с лыжником. Так как траектория – плоская линия, то ось В, направленную по бинормали, показывать не нужно (проекции на ось В действующих на лыжника сил будут равны нулю).

Дифференциальные уравнения по (5) получим такие

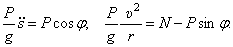(6)

Первое уравнение получилось нелинейным: 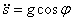. Так как 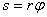, то его можно переписать так: 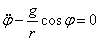. Такое уравнение можно один раз проинтегрировать. Запишем 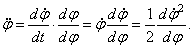Тогда в дифференциальном уравнении переменные разделятся: 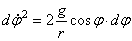. Интегрирование дает решение 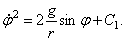Так как при t = 0: 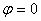и 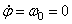, то С₁= 0 и 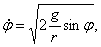а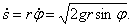

К сожалению, в элементарных функциях второй интеграл найти невозможно. Но и полученное решение позволяет сделать некоторые выводы. Можно найти скорость лыжника в любом положении как функцию угла 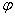. Так в нижнем положении, при 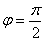, 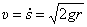. А из второго уравнения (6) при 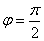можно определить давление: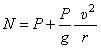 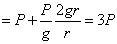. То есть давление на лыжника в нижнем положении равно его трехкратному весу.

Пример 6: Точка, имеющая массу m, движется из состояния покоя по окружности радиуса R с постоянным касательным ускорением 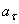. Определить действующую на точку силу в момент, когда она пройдет по траектории расстояние .

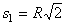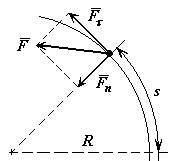
Рис.9

Решение: Применяя дифференциальные уравнения движения точки в проекциях на естественные оси, имеем:

; ; ;

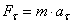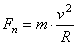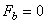Так как 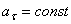, то ,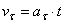

; ;

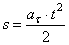
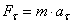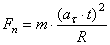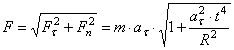
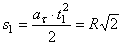; следовательно ;

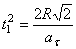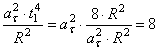; следовательно