Задачи для самостоятельного решения. 1.1. Средний срок службы мотора 4 года
1.1. Средний срок службы мотора 4 года. Оценить снизу вероятность того, что данный мотор не прослужит более 20 лет.
1.2. Среднее число дождливых дней в году в данном районе равно 80. Оценить вероятность того, что в этом районе будет не более 100 дождливых дней в году.
1.3. Средний вес клубня картофеля равен 120 г. Какова вероятность того, что наугад взятый клубень картофеля весит не более 300 г?
1.4. Сумма всех вкладов в некотором сберегательном банке составляет 2 млн. руб., а вероятность того, что случайно взятый вклад не превышает 10000 руб. равна 0,8. Что можно сказать о числе вкладчиков данного сберегательного банка?
1.5. Номинальное значение диаметра втулки равно 5 мм, а дисперсия, вследствие погрешностей изготовления, не превосходит 0,01. Оценить вероятность того, что размер втулки будет отличаться от номинала не более чем на 0,5 мм.
1.6. Случайная величина Х имеет дисперсию, равную 0,01. Какова вероятность того, что случайная величина Х отличается от математического ожидания не более чем на 0,25?
1.7. Случайная величина Х имеет закон распределения:
| хк | 4,5 | |||||
| рк | 0,1 | 0,4 | 0,3 | 0,05 | 0,05 | 0,1 |
Пользуясь неравенством Маркова, оценить вероятность того, что случайная величина Х примет значение, большее 4.
1.8. Электростанция обслуживает сеть из 18000 ламп, вероятность включения каждой из которых в зимний вечер равна 0,9. Оценить вероятность того, что число ламп, включенных в сеть зимним вечером, отличается от своего математического ожидания по абсолютной величине не менее, чем на 200.
1.9. Оценить вероятность того, что отклонение любой случайной величины от ее математического ожидания по модулю будет меньше трех средних квадратичных отклонений этой величины.
1.10. Определить сколько надо провести замеров диаметров деревьев, чтобы средний диаметр деревьев отличался от истинного значения не более, чем на 2 см с вероятностью не меньшей 0,95. Известно, что на данном участке среднеквадратическое отклонение диаметров деревьев не превышает 10см.
1.11. Оценить вероятность того, что число лиц, имеющих высшее образование, в группе из 800 человек отличается от своего математического ожидания меньше, чем на 30.
1.12. Для определения средней продолжительности горения электроламп в партии из 200 одинаковых ящиков было взято на выборку по одной лампе из каждого ящика. Оценить снизу вероятность того, что средняя продолжительность горения отобранных 200 ламп отличается от средней продолжительности горения во всей партии по абсолютной величине меньше, чем на 5 часов, если известно, что среднее квадратичное отклонение продолжительности горения любой лампы в каждом ящике меньше 7 часов.
1.13. Сколько раз нужно измерять данную величину, значение которой равно а, чтобы с вероятностью не меньшей, чем 0,95, можно было утверждать, что среднее арифметическое значений этих измерений отличается от а по абсолютной величине меньше, чем на 2, если среднеквадратическое отклонение каждого из измерений меньше 10?
1.14. Для определения урожайности поля из 200 га взяли выборку с каждого гектара. Известно, что по каждому гектару поля дисперсия не превышает 2. Оценить вероятность того, что отклонение средней выборочной урожайности не превосходит 0,2ц.
1.15. Вероятность положительного исхода отдельного испытания р =0,8. Оценить вероятность того, что в 1000 независимых повторных испытаниях отклонение относительной частоты положительных исходов от вероятности при отдельном испытании по абсолютной величине будет меньше 0,05.
1.16. Всхожесть семян некоторого растения составляет 60%. Найти вероятность того, что при посеве 10000 семян отклонение доли взошедших семян от вероятности того, что взойдет каждое из них, не превосходит 0,01.
1.17. В каких пределах находится случайная положительная величина Х с вероятностью 0,8, если ее математическое ожидание равно 2?
1.18. Пусть вероятность того, что покупателю обувного магазина необходимы туфли 41-го размера, равна 0,15. Оценить границы процента покупателей среди 2000 побывавших в магазине, которым нужны такие туфли, если эти границы надо гарантировать с вероятностью 0,98.
1.19. Среднее изменение курса акций в течение месяца составляет 0,5%. Оценить вероятность того, что в течение месяца курс акций изменится не более, чем на 2%.
1.20. Среднее количество звонков в офис фирмы в течение дня равно 30. Оценить вероятность того, что в течение дня появится более 90 звонков.
1.21. Сколько раз нужно бросить монету, чтобы с вероятностью не меньшей, чем 0,997, можно было утверждать, что относительная частота выпадения герба будет между 0,499 и 0,501?
1.22. Опыт страховой компании показывает, что на каждый пятый договор приходится страховой случай. Сколько договоров нужно заключить, чтобы с вероятностью 0,95 можно было утверждать, что доля страховых случаев отклонится от 0,2 не более, чем на 0,05?
1.23. Вероятность того, что акции, переданные на депозит, будут востребованы, равна 0,075. Оценить вероятность того, что из 1000 клиентов от 60 до 90 востребуют свои акции.
1.24. При установившимся технологическом процессе фабрика выпускает в среднем 80% продукции первого сорта. Чему равна вероятность того, что в партии из 1000 изделий число первосортных заключено между 760 и 830?
1.25. Посажено 600 семян кукурузы с вероятностью 0,9 прорастания для каждого семени. Найти границу абсолютной величины отклонения относительной частоты взошедших семян от вероятности р = 0,9, если эта граница должна быть гарантирована с вероятностью 0,995.
1.26. С конвейера сходит в среднем 85% изделий первого сорта, Определить, сколько изделий надо взять, чтобы с вероятностью 0,997 можно было утверждать, что относительная частота изделий первого сорта отличается от вероятности 0,85 по модулю не более, чем на 0,01.
1.27. Имеется 100 партий деталей. Математическое ожидание числа бракованных деталей в каждой партии равно 2, а среднеквадратическое отклонение равно 1,5. Найти вероятность того, что всего в 100 партиях имеется от 180 до 220 бракованных изделий.
1.28. При каком числе независимых испытаний вероятность выполнения неравенства 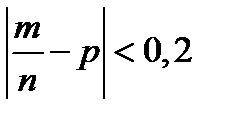 превысит 0,96, если вероятность появления события в отдельном испытании равна 0,7?
превысит 0,96, если вероятность появления события в отдельном испытании равна 0,7?
1.29. В среднем 10% работоспособного населения некоторого региона − безработные. Оценить с помощью неравенства Чебышева вероятность того, что уровень безработицы среди обследованных 10000 работоспособных жителей города будет в пределах от 9 до 11% (включительно).
1.30. Сколько нужно произвести измерений, чтобы с вероятностью, равной 0,9973, утверждать, что погрешность средней арифметической результатов этих измерений не превысит 0,01, если измерение характеризуется среднеквадратическим отклонением, равным 0,03?
