Определители квадратных матриц. Свойства определителей

ВОПРОСЫ К ЭКЗАМЕНУ

Понятие матрицы. Виды матриц. Операции над матрицами.

Матрицы. Действия над матрицами. Свойства операций над матрицами. Виды матриц.

Матрицей A=A_mn порядка m*n называется прямоугольная таблица чисел, содержащая m - строк и n - столбцов.

Элементы матрицы a_ij, у которых i=j, называются диагональными и образуют главную диагональ.

Для квадратной матрицы (m=n) главную диагональ образуют элементы a₁₁, a₂₂,..., a_nn .

Равенство матриц.

A=B, если порядки матриц A и B одинаковы и a_ij=b_ij (i=1,2,...,m; j=1,2,...,n)

Покажем операцию умножения матриц на примере

5. Возведение в степень

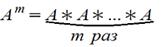
m>1 целое положительное число. А - квадратная матрица (m=n) т.е. актуально только для квадратных матриц

6. Транспонирование матрицы А. Транспонированную матрицу обозначают A^T или A'

Строки и столбцы поменялись местами.

Действия над матрицами.

Действия над матрицами.

1. Сложение матриц - поэлементная операция

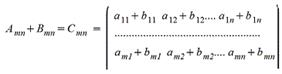
2. Вычитание матриц - поэлементная операция

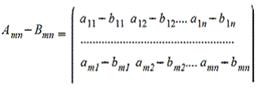
3. Произведение матрицы на число - поэлементная операция

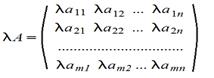
4. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B)

A_mk*B_kn=C_mn причем каждый элемент с_ij матрицы C_mn равен сумме произведений элементов i-ой строки матрицы А на соответствующие элемеенты j-го столбца матрицы B , т.е.

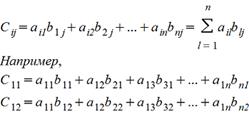
Определители квадратных матриц. Свойства определителей.

Каждой квадратной матрице размера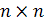

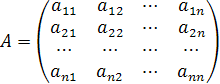
может быть поставлено в соответствие некоторое число, называемое определителем матрицы 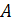, или просто определителем n-го порядка.

Определение. Определителем n-го порядка матрицы 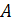называется число, равное алгебраической сумме n! слагаемых, каждое из которых равно произведению n элементов 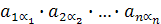матрицы 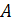, взятых по одному из каждой строки и каждого столбца, причем каждое слагаемое берется со знаком “+" или "-".

Определитель матрицы 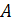обозначают различными символами: .

.

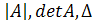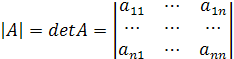Свойства определителей:

1. Определитель не изменится, если его строки заменить столбцами, и наоборот.

2. От перестановки двух строк или двух столбцов определитель изменит только знак.

3. Определитель, имеющий две одинаковые строки (два одинаковых столбца) равен нулю.

4. Общий множитель любой строки (столбца) можно вынести за знак определителя.

5. Определитель, у которого элементы двух строк (двух столбцов) соответственно пропорциональны, равен нулю.

6. Если каждый элемент какого-либо столбца (строки) определителя есть сумма двух слагаемых, то определитель равен сумме двух определителей. У одного из них элементами соответствующего столбца (строки) будут первые слагаемые, у другого – вторые. Остальные элементы у этих двух определителей те же, что и у данного.

7. Определитель не изменится, если к элементам любой строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.

8. Умножение всех элементов некоторой строки (столбца) определителя на число k равносильно умножению определителя на это число k.

9. Если все элементы некоторой строки (столбца) определителя равны нулю, то и сам определитель равен нулю.

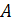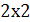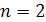Пример. Определителем второго порядка матрицы размера (где , а 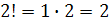, значит, определитель имеет два слагаемых) называется число равное 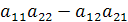. Обозначается

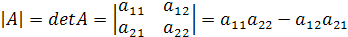
Мнемоническое правило вычисления определителя второго порядка:

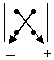Пример. Вычислить определитель матрицы .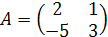

Решение. По формуле имеем:

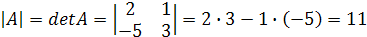
Пример. Вычислить определитель матрицы .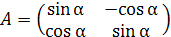

Решение. По формуле имеем:

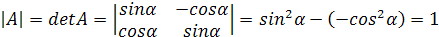
Матрице 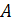размера 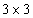соответствует число, называемое определителем третьего порядка матрицы .

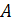Обозначается 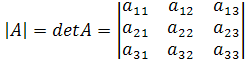и выражается через определители второго порядка.

Способы вычисления определителей третьего порядка:

а) разложение по элементам строк и столбцов:

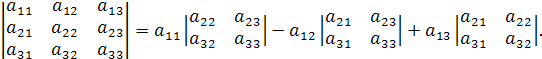
Замечание. Определитель третьего порядка можно раскрывать по любой строке или столбцу. Для этого необходимо применять правило с учетом знаков: элемент a_ij берут со знаком (–1)^i+j или запомнить таблицу

б) диагональный:

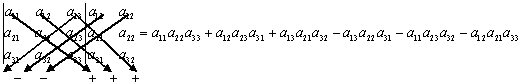Суть метода: приписываем справа первый и второй столбец соответственно; перемножаем со знаком «+» элементы главной диагонали и двух дополнительных диагоналей, со знаком «–» элементы побочной диагонали и двух дополнительных диагоналей.

в) «звездочка» – мнемоническое правило вычисления определителя третьего порядка:

слагаемые со знаком «+» слагаемые со знаком «-».

Пример. Вычислить определитель матрицы .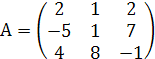

Решение. Воспользуемся формулой разложения определителя по элементам строк и столбцов, разложим по первой строке:

.

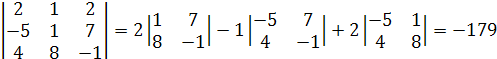Замечание. При вычислении определителей четвертого порядка и выше используется способ разложения по строке или столбцу.