Уравнения радиального равновесия
Влияние начального давления и темпиратуры пара на цикл КПД Ренкена
Идеальным термодинамическим циклом тепловых и атомных электростанций является цикл Ренкена.В ПДФ
Особености атомных ПТУ
Основные особенности паровой турбины АЭС с ВВЭР и РБМК связаны с ее работой на насыщенном паре и потому с относительно малым теплоперепадом (большой расход пара) и работой большей части ступеней на влажном паре. Соответствующий цикл паротурбинной установки где показана также необходимость сепарации и промперегрева между частью среднего давления (ЧСД) и частью низкого давления (ЧНД) турбины.
ЧСД турбины выполняется в виде одного цилиндра среднего давления (ЦСД), а ЧНД турбины состоит обычно из нескольких цилиндров низкого давления (ЦНД), причем каждый из них выполнен двухпоточным. Пар после ЦСД и сепаратора-промперегревателя поступает параллельно во все ЦНД. (Правильнее говорить именно ЧСД и ЦСД, так как речь идет о среднем давлении, хотя иногда, по аналогии с обычной теплоэнергетикой, головную часть турбины АЭС называют ЧВД и ЦВД.) В любых паровых турбинах, за исключением противодавленческих, приходится иметь дело с работой на влажном паре. Если для турбины ТЭС на перегретом паре это относится только к последним ступеням ЦНД, то для машины на насыщенном паре большая часть НД, то есть ступени после промежуточного перегрева пара между цилиндрами, работают на перегретом паре. Влияние влажности пара отрицательно сказывается на тепловой экономичности установки — внутренний относительный КПД турбины при работе на влажном паре уменьшается. Приближенно можно считать, что
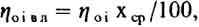
то есть увеличение средней влажности пара на 1% приводит к уменьшению внутреннего относительного КПД турбины также примерно на 1 %.
Влажность пара отрицательно влияет на работу турбины также и в связи с эрозией лопаток. Существуют методы отвода влаги из проточной части турбины. Конструкции внутритурбинных влагоудаляющих устройств различны.
Значительная часть влаги отбрасывается к корпусу по поверхности лопаток рабочего колеса, поэтому такие сепарационные устройства целесообразно располагать непосредственно за рабочим колесом, тогда отведенный конденсат уже не будет оказывать вредного влияния на работу последующих ступеней турбины. Для последней ступени ЦНД отводят влагу также и с помощью влагоулавливающего устройства, расположенного за сопловым аппаратом.
Для удаления влаги из влагоулавливающей камеры отсасывается некоторое количество пара, который направляется затем в регенеративную систему. Эффективность влагоудаления возрастает с увеличением отсоса, однако при этом возрастает недовыработка электроэнергии на отсасываемом паре. Хотя теоретически было бы целесообразно отводить влагу после каждой ступени, внутритурбинные влагоулавливающие устройства располагают только в ЦНД, где в связи с большими диаметрами проточной части турбины эрозионный износ лопаточного аппарата проявляется сильнее.
Эрозионные разрушения лопаток паровой турбины начинаются с их поверхности. Поэтому для снижения эрозии применяют различные способы упрочнения поверхности лопаток — хромирование, местную закалку кромок, нагартование, упрочнение поверхностного слоя электроискровым способом и др. На отечественных заводах наиболее распространен последний способ. Совершенно обязательно упрочнение поверхностного слоя лопаток для последних ступеней. Для этих целей используется стеллит, но бескобальтовый. Эффективность защитных мероприятий в решающей мере зависит от качества их выполнения, причем при плохом выполнении эрозия идет в еще большей мере, чем в отсутствие защитных мероприятий. В последние годы стали изготовлять лопатки для влажного пара из эрозионно-стойких материалов. Наряду с этим продолжаются поиски наиболее эффективных влагоудаляющих внутритурбинных устройств в сочетании с выбором более рациональных конструктивных и газодинамических параметров.
Наиболее эффективен вывод влаги через отборы турбины, особенно если число отборов отвечает числу ее ступеней. Уменьшение влажности при отводе влаги с греющим паром системы регенерации в процессах, изображаемых на h,s-диаграмме, обычно не учитывается. Это означает, что влажность по ступеням и за турбиной в действительности меньше, чем это следует из тепловых процессов в h,s — диаграмме.
10.
Основной задачей дальнейшего развития морских ГТД служит изыскание направлений для повышения их экономичности, которыми служат :повышение начальной (на выходе из камеры сгорания) температуры газа; применение промежуточного охлаждения сжимаемого в компрессорах ГТД воздуха; использование тепла выпускного газа для подогрева сжатого воздуха в затурбинном газовоздушном теплообменнике (регенерация тепла выпускного газа) перед его поступлением в камеру сгорания; использование тепла выпускного газа для получения пара в утилизационном парогенераторе теплоутилизационного контура с целью выработки в паровой турбине дополнительной мощности, отдаваемой потребителю механической энергии, основная часть мощности для которого отдается ГТД;
13. Si процесс в турбинной ступени.

Уравнения радиального равновесия
Паротурбинные ступени с q=d/l<10 (ступени большой веерности) относят к ступеням с длинными лопатками, в которых изменяются термодинамические параметры и кинематические характеристики потока водяного пара вдоль радиуса ступени (по высоте решеток). Эти изменения следует учитывать при профилировании проточной части сопловых и рабочих решеток, чтобы обеспечить высокий КПД ступени. На рис. 9.1,а показана проточная часть ступени большой веерности с меридиональными линиями тока и расчетными сечениями, а на рис. 9.1,б – параллелепипед абсолютных скоростей в цилиндрической системе координат. Для этих условий вектор скорости раскладывается на три составляющие: с2=сu2+ca2+cr2, которые связаны между собой через соответствующие углы: a, v и n. Чтобы спрофилировать лопатки для такой ступени, необходимо знать зависимости изменения параметров вдоль радиуса в зазорах между решетками. Для этого получим уравнение, связывающее изменение вдоль радиуса статического давления р1 со скоростью с1. Рассмотрим ступень, в которой линии тока расположены на цилиндрических поверхностях, т.е. составляющая сr=0. Будем считать, что поток в ступени осесимметричный, т.е. параметры потока в окружном направлении неизменны. Для вывода уравнения радиального равновесия выделенного элемента водяного пара рассматривается схема, показанная на рис. 9.1,в. в)

Рис. 9.1. К характеристике линий тока (а), скоростей (б) в ступени большой веерности и к выводу уравнения радиального равновесия потока в ней (в) Элемент потока толщиной da выделен в зазоре между цилиндрическими сечениями радиусами r и r+dr и меридиональными плоскостями с углом dj от оси ротора. К выделенному элементу приложены силы давления: - по цилиндрическим поверхностям + р1rdjda и – (р1+dр1)(r+dr)djda; - по меридиональным поверхностям (р1+0,5dp1)drda, а также инерционная сила от центростремительного ускорения элемента , где с1u – окружная составляющая скорости с1, v1 – удельный объем водяного пара в сечении «1-1» (рис. 9.1,а). Поскольку давление р1 вдоль оси а постоянно, то уравнение равновесия всех сил в проекциях на направление радиуса r имеет вид: р1×r×dj×da–(р1+dр1)(r+dr)×dj×da+2(р1+0,5dp1)×dr×da×sin+=0. (9.1) Заменив sin(dj/2)»dj/2, после преобразований (членами третьего порядка малости пренебрегаем) получим для сечения «1-1» ступени упрощенный вид уравнения радиального равновесия . (9.2) Аналогично получают уравнения и для других сечений («0-0» и «2-2» на рис. 9.1,а): ; . (9.3) Применительно к схеме течения, показанной на рис. 9.1,б, где присутствуют составляющие скорости по радиусу (с1r) и вдоль оси а (с1а), уравнение (9.2) записывается следующим образом: . (9.4) В правой части (9.4) первый член характеризует влияние центробежных сил, а остальные члены – влияние радиального ускорения. Из полученных уравнений радиального равновесия следует, что градиент статического давления вдоль радиуса в сечении за сопловой решеткой ступени пропорционален квадрату окружной составляющей скорости и обратно пропорционален радиусу. Таким образом, если перед ступенью (за ней) окружная составляющая скорости с0u (c2u) равна нулю, т.е. угол a0 (a2) равен 900, то по высоте лопаток перед ступенью (за ней) статическое давление не изменяется. На основе уравнений радиального равновесия формируются различные законы закручивания лопаток решеток турбинных ступеней.
19.
22. Особенности проектирования лопаток последней ступенисвязаны с прочностными характеристиками, большими окружными скоростями, большой влажностью.
25.
28. Деформацией называется изменение формы и размеров тела под действием напряжений.
Деформация металла под действием напряжений может быть упругой и пластической.
Упругой называется деформация, полностью исчезающая после снятия вызывающих ее напряжений.
При упругом деформировании изменяются расстояния между атомами металла в кристаллической решетке. Снятие нагрузки устраняет причину, вызвавшую изменение межатомного расстояния, атомы становятся на прежние места, и деформация исчезает.
Упругая деформация на диаграмме деформации характеризуется линией ОА (рисунок 5).

Рисунок 5 – Диаграмма зависимости деформации металла ε
от действующих напряжений σ
Если нормальные напряжения достигают значения сил межатомных связей, то наблюдается хрупкое разрушение путем отрыва (рисунок 6)

Рисунок 6 – Схема упругой деформации и хрупкого разрушения под действием упругих напряжений а – ненапряженная решетка металла; б – упругая деформация; в, г – хрупкое разрушение в результате отрыва
Зависимость между упругой деформацией ε и напряжением σ выражается законом Гука
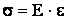
где Е – модуль упругости.
Модуль упругости является важнейшей характеристикой упругих свойств металла. По физической природе величина модуля упругости рассматривается как мера прочности связей между атомами в твердом теле.
Эта механическая характеристика структурно нечувствительна, т. е. термическая обработка или другие способы изменения структуры не изменяют модуля упругости, а повышение температуры, изменяющее межатомные расстояния, снижает модуль упругости.
Пластической или остаточной называется деформация после прекращения действия вызвавших ее напряжений.
При пластическом деформировании одна часть кристалла перемещается по отношению к другой под действием касательных напряжений. При снятии нагрузок сдвиг остается, т.е. происходит пластическая деформация (рисунок 7)
В результате развития пластической деформации может произойти вязкое разрушение путем сдвига.
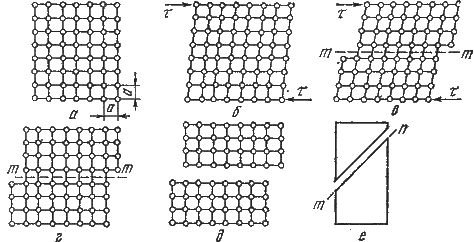
Рисунок 7 – Схема пластической деформации и вязкого разрушения под действием касательных напряжений а– ненапряженная решетка; б – упругая деформация; в – упругая и пластическая деформация; г – пластическая деформация; д, е – пластичное (вязкое) разрушение в результате среза
Процесс деформации при достижении высоких напряжений завершается разрушением. Тела разрушаются по сечению не одновременно, а вследствие развития трещин. Разрушение включает три стадии: зарождение трещины, ее распространение через сечение, окончательное разрушение.
Различают хрупкое разрушение – отрыв одних слоев атомов от других под действием нормальных растягивающих напряжений. Отрыв не сопровождается предварительной деформацией. Механизм зарождения трещины одинаков благодаря скоплению движущихся дислокаций перед препятствием (границы субзерен, фазовые границы), что приводит к концентрации напряжений, достаточной для образования трещины. Когда напряжения достигают определенного значения, размер трещины становится критическим и дальнейший рост осуществляется произвольно.
Для хрупкого разрушения характерна острая, часто ветвящаяся трещина. Величина зоны пластической деформации в устье трещины мала. Скорость распространения хрупкой трещины велика – близка к скорости звука (внезапное, катастрофическое разрушение). Энергоемкость хрупкого разрушения мала, а работа распространения трещины близка к нулю.
Различают транскристаллитное разрушение – трещина распространяется по телу зерна, интеркристаллитное – по границам зерен (всегда хрупкое).
Результатом хрупкого разрушения является блестящий светлый кристаллический излом с ручьистым строением. Хрупкая трещина распространяется по нескольким параллельным плоскостям. Плоскость излома перпендикулярна нормальным напряжениям.
Вязкое разрушение – путем среза под действием касательных напряжений. Ему всегда предшествует значительная пластическая деформация.
Трещина тупая раскрывающаяся. Величина пластической зоны впереди трещины велика. Малая скорость распространения трещины. Энергоемкость значительная, энергия расходуется на образование поверхностей раздела и на пластическую деформацию. Большая работа затрачивается на распространение трещины. Поверхность излома негладкая, рассеивает световые лучи, матовая (волокнистый) излом. Плоскость излома располагается под углом.
По излому можно определить характер разрушения.
Механические свойства металлов и сплавов. К механическим свойствам металлов и сплавов относятся: прочность, твердость, упругость, пластичность, ударная вязкость, ползучесть и усталость.

Рис. 76. Виды нагрузок, вызывающих изменение формы металла или cплава
Прочность - это способность металла или сплава противостоять деформации и разрушению под действием приложенных нагрузок - растягивающих, сжимающих, изгибающих, скручивающих и срезающих (рис. 76). Нагрузки бывают внешними (вес, давление и др.) и внутренними (изменение размеров тела от нагревания и охлаждения, изменение структуры металла и т. д.), а также статическими, т. е. постоянными по величине и направлению действия, или динамическими, т. е. переменными по величине, направлению и продолжительности действия. Методы определения прочности рассмотрены отдельно.
Твердостью называется способность металла или сплава оказывать сопротивление проникновению в него другого, более твердого тела. Применяют следующие способы испытания твердости металлов и сплавов вдавливанием в поверхность образца:
стального закаленного шарика диаметром 2,5; 5 или 10 мм - определение твердости по Бринеллю;
стального закаленного шарика диаметром 1,588 мм или алмазного конуса с углом 120° - определение твердости по Роквеллу;
правильной четырехгранной алмазной пирамиды – определение твердости по Виккерсу.
Упругостью называется способность металла или сплава восстанавливать первоначальную форму после прекращения действия внешней нагрузки (рис. 77).

Рис. 77. Деформация, характеризующая упругость (после снятия нагрузки образец возвращается в исходное положение)
Пластичностью называется способность металла или сплава, не разрушаясь, изменять форму под действием нагрузки и сохранять эту форму после ее снятия.
Ударной вязкостью называется способность металла или сплава сопротивляться действию ударных нагрузок. Ударная вязкость измеряется в кгс•м/см2 (Дж/м2).
Ползучестью называется свойство металла или сплава медленно и непрерывно пластически деформироваться под действием постоянной нагрузки (особенно при повышенных температурах).
Усталостью называется постепенное разрушение металла или сплава при большом числе повторно-переменных нагрузок; свойство выдерживать эти нагрузки называется выносливостью.
Испытания образцов металлов и сплавов на растяжение. При испытании образцов на растяжение определяют предел прочности (временное сопротивление) σв, предел текучести (физический) σт, предел текучести условный (технический) σ0,2, предел пропорциональности σпц, истинное сопротивление разрыву Sк и относительное удлинение и сужение δ, φ.

Рис. 78. Диаграмма растяжения (зависимость удлинения ∆l от нагрузки Р)
Рассмотрим показанную на рис. 78 диаграмму, на которой по вертикальной оси отложена приложенная нагрузка Р в килограммах (чем выше точка по оси, тем больше нагрузка), а по горизонтальной оси - абсолютное удлинение ∆l образца. Такие диаграммы строят по результатам растяжения образцов на специальных испытательных разрывных машинах. Полученная кривая позволяет судить о прочности образца на растяжение.
Начальный прямолинейный участок 0-Рпц характеризует упругость образца, пропорциональность между удлинением материала и нагрузкой (Рпц - нагрузка при пределе пропорциональности).
Точка Р׳т резкого перегиба кривой определяет величину нагрузки при верхнем пределе текучести. Участок Р׳т-Рт (площадка текучести), параллельный горизонтальной оси 0-∆l, в пределах которого образец удлиняется при постоянной внешней нагрузке.
Точка Рв отмечает наибольшую растягивающую силу - нагрузку при пределе прочности, по которой рассчитывают предел прочности материала образца.
Точка Рк определяет величину растягивающей силы в момент разрушения образца.
Предел прочности при растяжении (временное сопротивление) - это напряжение, отвечающее наибольшей нагрузке, предшествовавшей разрушению образца: σв=Pв/F0, где F0 - площадь поперечного сечения образца перед испытанием, мм2 (м2); Рв - наибольшая растягивающая сила, кгс (Н).
Предел текучести (физический) - это наименьшее напряжение, при котором происходит деформация испытуемого образца без увеличения нагрузки (нагрузка не увеличивается, а образец удлиняется): σт=Pт/F0, где Рт – нагрузка растяжения, вызывающая удлинение образца на площадке текучести, кгс (Н).
Предел текучести условный (технический) σ0,2 – это напряжение, при котором остаточная деформация образца достигает 0,2%: σ0,2= Р׳т/F0, где Рт - нагрузка растяжения в начале площадки текучести, кгс (Н).
Предел пропорциональности σпц - условное напряжение, при котором отступление от линейной зависимости между напряжениями и деформациями достигает определенной степени, устанавливаемой техническими условиями: σпц=Рпц/F0, где Рпц - нагрузка в конце площадки упругости, кгс (Н).
Истинное сопротивление разрыву - это напряжение в шейке растягиваемого образца, определяемое как отношение растягивающей силы, действующей на образец непосредственно перед его разрывом, к площади поперечного сечения образца в шейке: Sк=Pк/F, где Рк - нагрузка в момент разрыва образца, кгс (Н); F - истинное сечение образца в момент разрыва, мм2 (м2).
Относительное удлинение δ и относительное сужение – φ определяются по формулам: δ=∆l/l0∙100%, φ=(F0-F)/F∙100%, где ∆l=l1-l0 - абсолютное удлинение образца при разрыве; l1 - длина образца в момент разрыва; l0 - первоначальная длина образца; F0 – первоначальная площадь поперечного
Под длительной прочностью понимается сопротивление металлов и сплавов механическому разрушению под действием постоянной длительной нагрузки, т. е. в условиях ползучести. Количественной ее характеристикой является предел длительной прочности 0П, т. е. наименьшее напряжение, вызывающее разрушение при заданных техническими условиями температуре и^времени, например, при 600° С за 1000 ч. В этом случае предел длительной прочности можно обозначить а 6Д°°0С в кГ/мм2
31.
34.Уравнения Навье — Стокса — система дифференциальных уравнений в частных производных, описывающая движение вязкой ньютоновской жидкости. Уравнения Навье — Стокса являются одними из важнейших вгидродинамике и применяются в математическом моделировании многих природных явлений и технических задач. Названы по имени французского физика Анри Навье и британского математика Джорджа Стокса.
В случае несжимаемой жидкости система состоит из двух уравнений:
· уравнения движения,
· уравнения неразрывности.
В гидродинамике обычно уравнением Навье — Стокса называют только одно векторное уравнение движения[1][2][3][4][5][6]. Впервые уравнение Навье — Стокса было получено Навье (1827, несжимаемая жидкость[7]) иПуассоном (1831, сжимаемая жидкость[8]), которые исходили из модельных представлений о молекулярных силах. Позже феноменологический вывод уравнения был дан Сен-Венаном[9] и Стоксом[10].
В векторном виде для несжимаемой жидкости они записываются следующим образом:
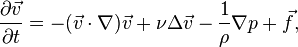
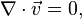
где  — оператор набла,
— оператор набла, 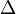 — векторный оператор Лапласа,
— векторный оператор Лапласа, 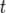 — время,
— время,  — коэффициент кинематической вязкости,
— коэффициент кинематической вязкости,  — плотность,
— плотность,  — давление,
— давление, 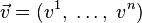 — векторное поле скоростей,
— векторное поле скоростей, 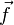 — векторное поле массовых сил. Неизвестные
— векторное поле массовых сил. Неизвестные  и
и  являются функциями времени
являются функциями времени 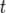 и координаты
и координаты 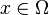 , где
, где 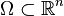 ,
,  — плоская или трёхмерная область, в которой движется жидкость. Обычно в систему уравнений Навье — Стокса добавляют краевые и начальные условия, например:
— плоская или трёхмерная область, в которой движется жидкость. Обычно в систему уравнений Навье — Стокса добавляют краевые и начальные условия, например:
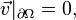
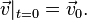
Иногда в систему уравнений Навье — Стокса дополнительно включают уравнение теплопроводности и уравнение состояния.
При учёте сжимаемости уравнения Навье — Стокса принимают следующий вид:
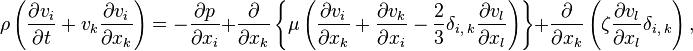

где 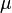 — коэффициент динамической вязкости (сдвиговая вязкость),
— коэффициент динамической вязкости (сдвиговая вязкость),  — «вторая вязкость», или объёмная вязкость,
— «вторая вязкость», или объёмная вязкость, 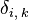 — дельта Кронекера.
— дельта Кронекера.
Уравнения Рейнольдса (англ. RANS (Reynolds-averaged Navier-Stokes)) — уравнения Навье-Стокса (уравнения движения вязкой жидкости) осредненные по Рейнольдсу.
Используются для описания турбулентных течений. Метод осреднения Рейнольдса заключается в заменеслучайно изменяющихся характеристик потока (скорость, давление, плотность) суммами осредненных ипульсационных составляющих. В случае несжимаемой Ньютоновской жидкости уравнения Рейнольдсазаписываются в виде:
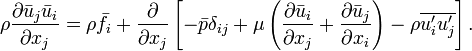
Переменные, осредненные по времени, отмечены в этом уравнении чертой сверху, а пульсационныесоставляющие — апострофом. Левая часть уравнения (нестационарный член) описывает изменениеколичества движения жидкого объёма, вследствие изменения во времени осредненной составляющейскорости. Это изменение компенсируется (см. правую часть уравнения) осредненными внешними силами  , осредненными силами давления
, осредненными силами давления 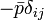 , вязкостными силами
, вязкостными силами 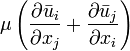 . Кроме того, в правуючасть входят кажущиеся напряжения (напряжения Рейнольдса, турбулентные напряжения)
. Кроме того, в правуючасть входят кажущиеся напряжения (напряжения Рейнольдса, турбулентные напряжения) 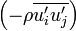 , учитывающие дополнительные потери и перераспределение энергии в турбулентном потоке (по сравнениюс ламинарным потоком).
, учитывающие дополнительные потери и перераспределение энергии в турбулентном потоке (по сравнениюс ламинарным потоком).
Уравнения Рейнольдса описывают осредненное по времени течение жидкости, их особенность (посравнению с исходными уравнениями Навье-Стокса) заключается в том, что в них появились новыенеизвестные функции, которые характеризуют кажущиеся турбулентные напряжения. Система уравненийРейнольдса содержит шесть неизвестных и оказывается незамкнутой, в связи с чем, для её решенияприходится привлекать дополнительную информацию.
Весьма существенным является то обстоятельство, что напряжения Рейнольдса являются случайнымивеличинами, поэтому в расчетах используют статистические данные об их величине (моделитурбулентности), которые получают путём анализа результатов эксперимента. Также необходимоотметить, что напряжения Рейнольдса являются свойством течения (а не свойством жидкости), поэтому, если условия рассматриваемой задачи будут существенно отличаться условий, в которых были полученыстатистические данные о величине напряжений Рейнольдса, результаты расчёта могут оказатьсякачественно неверными. К настоящему времени разработано значительное количество моделейтурбулентности различной сложности, позволяющих оценить (смоделировать) величину турбулентныхнапряжений в различных условиях.
