III. Метод волосного гигрометра

Действие волосного гигрометра основано на свойстве челове­ческого волоса поглощать влагу и изменять свою длину в зависимости от изменений относительной влажности воздуха. Во влажном воздухе волос, набухая, удлиняется, а в сухом воздухе - уко­рачивается.

Конструктивно волосной гигрометр оформляется следующим образом. Хорошо очищенный и обезжиренный конский волос верхним концом прикрепляется к рамке прибора, нижним концом - к дужке, вращающейся около оси. Дужка связана с пружиной, благодаря че­му волос всегда поддерживается в натянутом состоянии. На этой же оси укреплена стрелка, связанная с дужкой. Конец стрелки перемещается вдоль шкалы с делениями, обозначающими проценты относительной влажности воздуха от 0 до 100%.

Для того чтобы волосной гигрометр давал верные показания, его время от времени проверяют, сравнивая его показания c пока­заниями аспирационного психрометра Ассмана.

Существенным преимуществом волосного гигрометра является то, что он позволяет определять влажность воздуха не только при положительных, но и при отрицательных температурах воздуха. Поэтому в зимних условиях волосной гигрометр служит единственным прибором, с помощью которого на метеорологических станциях производятся наблюдения за изменениями влажности воздуха.

На принципе действия волосного гигрометра основано уст­ройство гигрографа - прибора, предназначенного для непрерыв­ной записи изменений относительной влажности воздуха. Гигро­графы применяются на метеорологических станциях, в научных лабораториях, складах.

Приемной частью гигрографа служит пучок хорошо очищен­ных и обезжиренных женских волос в количестве 30-40 штук. При увеличении относительной влажности воздуха пучок волос удлиняется, а при уменьшении относительной влажности воздуха – уко­рачивается. Изменение длины пучка волос передается при помощи рычагов стрелке, снабженной пером. Перо производит запись по­казаний прибора на ленте, надетой на барабан, который приво­дится в движение часовым механизмом. Полный оборот барабана происходит за 176 часов (1 неделя и 6 часов). Его показания периодически сверяются с показаниями психрометра Ассмана. При определении относительной влажности воздуха по гигрографу не следует трогать его руками.

Порядок выполнения работы

В задачу данной части лабораторной работы входит проверка волосного гигрографа и гигрометра, в процессе которой устанав­ливаются поправки к показаниям данных приборов.

Будем считать поправкой к показанию прибора величину Dr, которую необходимо прибавить к показанию прибора r', чтобы получить истинное значение относительной влажности воздуха r. Таким образом,

r'+Dr = r,

отсюда

Dr = r– r'. (11)

Поправка Dr может быть как положительной, так и отрицатель­ной.

Результаты измерений свести в следующий протокол.

1. Поверка волосного гигрометра:

а) показание волосного гигрометра- r' (%);

б) относительная влажность воздуха, определенная с помощью аспирационного психрометра Ассмана - r (%);

в) поправка к показанию волосного гигрометра - Dr (%).

2. Поверка гигрографа:

а) показание гигрографа - r' (%);

б) относительная влажность воздуха, определенная с помощью аспирационного психрометра Ассмана - r (%);

в) поправка к показанию гигрографа - Dr (%).

Литература

1. Савельев И.В. Курс общей физики. Т. I. -М.: Наука, 1977. § 1.

2. Телеснин Р.В. Молекулярная физика. - М.: Высшая школа, 1965. § 63.

3. Ландсберг Г.С. Элементарный учебник физики. Т. I. - М.: Наука, 1967.

4. Физический практикум (механика и молекулярная фи­зика)/ Под ред. В.И.Ивероновой. - М.: Наука, 1967. Задача 59.

5. Мэрион Дж.Б. Общая физика с биологическими примерами. - М.: Высшая школа, 1986.

Для получения зачета необходимо

1. Продемонстрировать умение определять разными методами влаж­ность воздуха.

2. Представить отчет по установленной форме.

3. Уметь отвечать на вопросы типа:

а) Почему в радиопередачах метеосводки объявляют об относи­тельной, а не об абсолютной влажности воздуха?

б) Чем объяснить то, что вечером после жаркого летнего дня в низменной местности наблюдается образование тумана?

в) На улице целый день моросит холодный осенний дождь. В ком­нате развесили выстиранное белье. Высохнет ли белье быстрее, если открыть форточку?

г) При каких условиях при росте абсолютной влажности может происходить уменьшение относительной влажности?

д) Чем объяснить то, что при открывании зимой форточки в комнату "врываются" клубы водяного тумана?

е) Почему запотевают очки, когда человек с мороза входит в комнату?

ж) Чем объяснить появление зимой инея на оконных стеклах? С какой стороны стекла он появляется? Почему?

з) Как изменится разность температур "сухого" и "влажного" термометров в психрометре при понижении температуры в комнате, если абсолютная влажность остается без изменения?

и) Почему зимой выделение тумана при дыхании заметно, а летом нет?

Дополнительные вопросы для студентов факультета технологии и предпринимательства

1. Почему открытые газопроводные трубы на зиму утепляют?

2. Какой процент влажности воздуха считается нормальным для человека, работающего в помещении механического цеха? Какое влияние оказывает на человека воздух с влажностью менее 30%? Как повысить влажность воздуха, если в помещении она составляет 20%?

3. Как влияет недостаточная относительная влажность воздуха на станки, инструменты и другие приборы в помещении?

4. Для чего желательно окрашивать фундаменты металлических станков и некоторые части станков?

Дополнительные вопросы для студентов факультетов химии, биологии, института естествознания

1. Как влияет на организм человека воздух повышенной (пониженной) влажности? Что означают термины: "воздух сухой", "воздух влажный, удушливый"? Дайте характе­ристику комфортной (с учетом влажнос­ти) для человека среды.

2. Почему и как образуется изморозь?

3. В настоящее время насчитывают около 600 видов животных и более 400 видов растений, которые могут выполнять роль барометров, индикаторов влажности и температуры, предсказателей штормов, бурь или хорошей безоблачной погоды. Приведите известные вам примеры.

Дополнительные вопросы к работе

1. Указать температуру, при которой в комнате не может быть увеличения влажности.

2. Какова размерность постоянной психрометра?

3. Как зависит давление насыщенных паров от темпе­ра­туры?

4. При каком режиме работы холодильника темпе­ратура наиболее медленно приближается к точке росы?

5. Вычислить плотность водяного пара, если его дав­ле­ние 1200 Па.

6. До какой температуры в воздухе с давлением водя­ного пара 800 Па охладится влажное тело?

7. Какой газ называется паром?

8. Чем отличается насыщенный пар от ненасыщен­ного?

9. Подчиняется ли пар газовым законам и каким?

10. Каковы устройства и принцип работы гигрометра и психрометра?

11. При температуре 300 K влажность воздуха 30%. При какой температуре влажность этого воздуха будет 50%?

12. Относительная влажность воздуха при темпе­ра­туре 293 K равна 44%. Что показывает влажный термометр психрометра?

13. Относительная влажность воздуха при темпера­туре 273 K равна 40%. Выпадет ли иней, если температура почвы понизится до 265 K? Почему?

14. Относительная влажность:

а) увеличивается с повышением температуры;

б) равна значению давления насыщенного пара;

в) при точке росы равна 100%;

г) указанные положения не действительны.

Выберите правильный ответ.

15. Как можно уменьшить относительную влажность воздуха в цехе, несмотря на увеличение абсолютной влажности?

Работа № 11. ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ТЕП­ЛО­ЕМКОСТЕЙ ВОЗДУХА МЕТОДОМ КЛЕМАНА-ДЕЗОРМА

Цель работы: опытное определение отношения теплоемкости воздуха при постоянном давлении С_P к теплоемкости при постоян­ном объеме С_V методом адиабатического расширения.

Принадлежности: прибор Клемана-Дезорма, манометр, секундомер, ручной насос.

Вопросы, знание которых обязательно для допуска

К выполнению работы

1. Что такое идеальный газ? Какие макроскопические и микроскопические параметры характе­ризуют состояние газа?

2. Какой процесс называется изотермическим, изобарическим, изохоричес­ким, адиабатическим? Приведите их графики в координатах Р-V; Р-T; V-T.

3. Что называется удельной (молярной) теплоемкостью?

4. Почему теплоемкость газов зависит от процесса?

5. Что понимают под числом степеней свободы молекул?

6. Сформулируйте первое начало термодинамики.

7. Какой принцип положен в основу вычисления С_P/С_V в данной работе?

8. Знать порядок выполнения работы.

В в е д е н и е

Количество теплоты, необходимое для нагревания тела на один градус, называют теплоемкостью тела. Количество теплоты, необходимое для нагревания единицы массы вещества на один градус, называют удельной теплоемкостью тела:

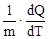с = . (1)

Формула (1) представлена в дифференциальной форме потому, что удельная теплоемкость реальных тел и газов зависит от температуры. Поскольку количество теплоты зависит от процесса, то и теплоемкость существенно зависит от процесса.

Молярная теплоемкость вещества – теплоемкость одного моля этого вещества:

С = 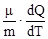, (2)

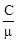c = , (3)

где m - молярная масса.

Рассмотрим теорию теплоемкости идеального газа.

Величина теплоемкости, характеризующая свойства газов, не является для данного газа величиной постоянной, а зави­сит от условий, при которых про­ис­ходит нагревание. Эту зависи­мость можно получить, воспользовав­шись первым началом термодинамики, которое формулируется следующим образом:

Количество теплоты dQ, переданное системе, затрачивается на увеличение ее внутренней энергии dU и на работу dА, совершае­мую системой против внешних сил:

dQ = dU + dA = dU + PdV. (4)

Если нагревание газа происходит при постоянном объеме, то газ не совершает работы (PdV = 0) и, следовательно, согласно первому началу термодинамики, все количество теплоты идет на увеличение внутренней энергии газа:

dQ = dU. (5)

Внутренняя энергия одного моля идеального газа

U = 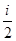RT, (6)

где i – число степеней свободы молекулы газа, R – универсальная газовая постоянная.

Теплоемкость одного киломоля идеального газа при постоянном объеме

C_V = 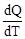= = 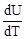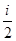R. (7)

Если нагревание газа происходит при постоянном давлении, то газ, расширяясь, совершает положительную работу против внешних сил. В соответствии с первым началом термодинамики (4) при изобарическом процессе подведенное количество теплоты расходуется на изменение внутренней энергии газа (dU) и совершение работы (dA), связанное с расширением газа:

dQ = dU + PdV. (8)

Из уравнения Клапейрона

PV = RT (9)

следует

PdV = RdT (10)

и

dQ = dU + RdT. (11)

Отсюда молярная теплоемкость при постоянном давлении

C_P = 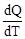= 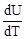+ R, (12)

где C_V = 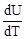- молярная теплоемкость при постоянном объеме. Следовательно,

C_P = C_V + R. (13)

Это - уравнение Майера, связывающее теплоемкости изобарного и изохорного процессов: молярная теплоемкость идеального газа при постоянном давлении больше молярной теплоемкости при постоянном объеме на величину универсальной газовой постоянной R.

В классической теории теплоемкость идеального газа определяется числом степеней свободы молекул и не зависит от температуры. Для одноатомного газа (i = 3) C_V = 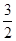R, C_P = 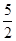R; для двухатомного (i = 5) C_V = 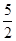R, C_P = 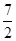R.

Если процесс перехода системы из одного состояния в другое протекает без теплообмена с окружающей средой, то такой процесс называется адиабати­чес­ким. При таком процессе уравнение (4) примет вид

dU + dA = 0

или

dA = -dU, (14)

т.е. при адиабатическом расширении или сжатии работа совершает­ся газом только за счет изменения запаса внутренней энергии. Уравнение адиабатического процесса (уравнение Пуассона) может быть выведено следующим образом. Поскольку dA = PdV, a dU = C_VdT, то уравнение (14) принимает вид:

PdV = - C_V dT. (15)

Разделив это уравнение на (9), получим

= -

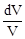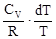
или

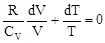. (16)

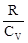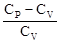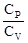Учитывая уравнение Майера, получим выражение для множителя = = – 1.

Если обозначить 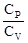= g, то уравнение (16) примет вид

(g - 1) 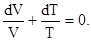(17)

Интегрируя и потенцируя уравнение (17), находим

ln V^g-1 + ln T = const,

T×V^g-1 = const. (18)

Используя уравнение состояния (9), получим уравнение Пуассона

P×V^g = const. (18)

Величина g зависит только от числа степеней свобо­ды молекул, из которых состоит газ.

Значения удельной теплоемкости некоторых газов приведены в таблице 1.

Таблица 1

Газ	Сv, Дж/кг К	Сp, Дж/кг К	g = Сp/Сv
He			1.66
Ar			1.67
H2			1.41
N2			1.40
O2			1.40
CO			1.40
NH3			1.31
CO2			1.30

Адиабатический процесс можно осуществить на следующей установке (рис. 1). В большой закрытый баллон Б, соединенный с U-образным открытым водяным манометром М, насосом Н нагнетается воздух. Через время t в нем уста­но­вится давление

Р₁=Н+h₁, (20)

где Н - атмосферное давление; h₁ - избыток давления воздуха в баллоне над атмосферным Н, измеряемый манометром и равный разности уровней жидкости в манометре.

Затем, если открыть кран П, то сжатый воздух быстро выйдет наружу, так как кран имеет довольно большое отверстие. Как толь­ко давле­ние в баллоне снизится и станет равным атмосферному (Н) - кран быстро закры­вают. Такой про­цесс расширения мож­но считать адиа­ба­тичес­ким, так как он протекает быстро и потому без теплообмена.

Пусть масса воздуха после накачивания насосом в баллоне объемом V₁ равна m. При открывании крана часть воздуха (Dm) выходит. Тогда масса оставшегося воздуха m₁ = m - Dm. Масса воз­духа m₁, которая заключается в объеме V₁, занимала перед открытием крана меньший объем V₂. Таким образом, уравнение (19) для массы газа m₁ в нашем случае, примет вид:

HV₁^g = P₁V₂^g, (21)

где Н и V₁ - давление и объем воздуха в конце процесса; P₁ и V₂ - давление и объем той же массы газа в начале процесса.

При адиабатическом расширении воздух в сосуде несколько охладится, но через некоторое время вследствие теплопроводности стенок температура воздуха начнет изохорически повышаться и снова станет равной температуре окружающей среды, а давление поднимется до величины P₂ = H + h₂ (h₂ - дополнительное давление, измеряемое манометром).

Начальное и конечное состояния газа наблюдаются при одина­ковой темпе­ратуре. Поэтому на основании закона Бойля-Мариотта получим

P₁V₂ = P₂V₁. (22)

Решив соответственно уравнения (21) и (22), получим

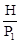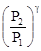= . (23)

Логарифмируя(23), найдем

lg H – lg P₁ = g×(lg P₂ – lg P₁),

откуда

g = 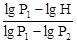. (24)

Поскольку на практике давления Н, Р₁ и Р₂ незначительно отличаются друг от друга, то в последней формуле разности логарифмов можно заменить разнос­тя­ми самих величин:

g = 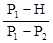. (25)

Если учесть, что P₁ = H + h₁, а Р₂ = Н + h₂ , из уравнения (25) получим расчетную формулу для данного опыта:

g = 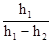. (26)

Рассмотренный метод определения отношения Сp/Сv может дать значение, близкое к табличному, только для случая малых сжатий и расширений газа в сосуде.

Порядок выполнения работы

1. В стеклянный баллон накачайте немного воздуха. Когда разность уровней в манометре станет максимальной, перекройте кран К. При закачивании воздуха совершается работа против сил давления газа, что приводит к увеличению его внутренней энергии, а следовательно, и температуры. Необходимо выж­дать 2-3 минуты (пока за счет теплообмена температура в баллоне не станет равной комнатной, при этом установится давление воздуха и разность уровней жидкости в манометре перестанет меняться), измерить мано­метром избыточное давление воздуха h₁.

2. Откройте кран П, соединяющий стеклянный баллон с атмосферой, и в тот момент, когда уровни жидкости в обоих коленах манометра М сравняются, быстро закройте кран. При этом происходит адиабатическое расширение воздуха, и чтобы оно было ближе к идеальному, п. 2 необходимо выполнить максимально быстро.

3. Выждав 2-3 минуты, пока газ, охлажденный при адиабати­ческом расширении, нагреется до комнатной температуры и давление окончательно установится, измерить избыточное давление[2] h₂.

4. По формуле (26) вычислить значение g.

5. Опыт повторите не менее 5 раз, изменяя всякий раз величину h₁ и определяя g, рассчитайте среднее зна­чение g_ср.

6. Если несколько первых значений g существенно отличаются друг от друга и от табличного, то это означает отсутствие навыка в проведении опыта (пробка закрывается слишком рано или слишком поздно). В этом случае для вычисления g следует при­менить метод экстраполяции. Для этого необходимо провести все те же изме­рения, что и в пунктах 1-4, но пробку вынимать не на 1-2 с, а на большие промежутки времени, отсчитываемые по секундомеру (пробку вынимать на 5, 10, 15 и 20 с). Первоначальное избыточ­ное давление по возможности устанавливать одно и то же. Опыт повторить по 3 раза для каждого промежутка времени. Данные из­мерений занести в таблицу 2. После этого построить график зависимости g_ср = f(t). Экстра­полируя (продолжая) график к t = 0, найдите g.

7. Подсчитать абсолютную и относительную погрешность в оп­ределении g.

8. Рассчитать охлаждение газа 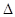Т при адиабатическом расширении. (Атмосферное давление определить по показаниям барометра; давление, измеренное в мм водяного столба, перевести в единицы СИ).

Таблица 2

t, c	№ опыта	h1, см	h2, см	g	gср
среднее
среднее
среднее
среднее

9. Определить удельную (молярную) теплоемкость воздуха при постоянном объеме и постоянном давлении (m_возд = 0.029 кг/моль).

Литература

1. Савельев И.В. Курс общей физики. Т.1. -М.: Наука, 1987.

2. Мелешко Л.О. Молекулярная физика и введение в термо­динамику. - Минск: Высшая школа, 1977.

3. Грабовский Р.Н. Курс физики. -М.: Высшая школа, 1970. § 42-44.

4. Мэрион Дж.Б. Общая физика с биологическими примерами. - М.: Высшая школа, 1986. Гл. 8, 9.

5. Ланина И.Я., Соломин В.П. Экскурсии в природу по физике и биологии. – СПб.: РГПУ им. А.И. Герцена, 1998.

6. Каленникова Т.Г. Природа и ты. (Вопросы и задания по экологии). - Минск: Народная Асвета, 1989.