Работа № 4. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

Цель работы - изучение особенностей протекания переходных процессов в электрических цепях, содержащих накопители энергии, получение представления об условиях существования установившихся режимов в цепи и их связи с вынужденным режимом.

1. Основные положения теории

Цепи, содержащие только резистивные элементы, не накапливают электрической энергии, для них связь между реакцией и воздействием описывается постоянным коэффициентом, который не зависит от предшествующего состояния цепи и определяется схемой соединения и параметрами резистивных элементов.

По-иному ведут себя электрические цепи, содержащие реактивные накопители электрической энергии (индуктивности, емкости). В этом случае энергия, вырабатываемая источниками, или необратимо преобразуется в другой вид энергии, или расходуется при совершении работы, или накапливается в цепи на реактивных накопителях. При этом реакция цепи на внешнее воздействие зависит не только от характера этого воздействия, но и от запасов энергии на реактивных накопителях.

Процессы, связанные с изменением энергии на накопителях, называют переходными процессами.

Практически все цепи, содержащие реактивные элементы, все время находятся в переходном режиме. Тем не менее, существуют режимы в электрических цепях, при которых запасы энергии на реактивных элементах практически не меняются, либо меняются по некоторому периодическому закону (в этом случае не меняется среднее значение энергии за период, запасенное в реактивных элементах). Такие режимы называют установившимися или квазиустановившимися, они возникают в цепях, содержащих источники с постоянными или периодически изменяющимися во времени параметрами.

Переходные процессы в линейных электрических цепях описываются линейными дифференциальными уравнениями. Полное решение этих уравнений обычно рассматривают как сумму общего и частного решений. Частное решение не зависит от запасов энергии на реактивных элементах и определяется внешними источниками, а также конфигурацией и параметрами элементов цепи. Оно получило название принужденной составляющей. Общее же решение в основном определяется состоянием реактивных накопителей, их запасами энергии, его форма не зависит от внешних источников, оно получило название свободной составляющей.

Форма решения для свободной составляющей зависит от корней характеристического уравнения и может быть представлена в виде 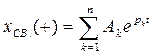. Следует заметить, что практически во всех случаях действительная часть корней характеристического уравнения отрицательна, а это говорит о том, что свободная составляющая с течением времени затухает.

В линейных цепях существование корней с нулевой действительной частью возможно лишь в цепях без потерь, состоящих только из реактивных элементов. В этом случае в цепи возникают незатухающие колебания. Так как на практике таких цепей не существует, их исследование носит чисто теоретический характер.

Особый интерес представляют цепи с активными необратимыми элементами (операционные усилители и др.), которые с точки зрения теории можно рассматривать как цепи, содержащие элементы с отрицательными параметрами. В этом случае характеристическое уравнение имеет корни с положительной действительной частью, при этом свободная составляющая может неограниченно возрастать.

В реальных цепях этот режим невозможен, так как на определенном этапе цепь переходит в нелинейный режим, при котором прекращается дальнейшее нарастание свободной составляющей.

В данной лабораторной работе такие режимы не рассматриваются. Так как в пассивных цепях с потерями свободная составляющая всегда затухает, по ее затуханию оценивают длительность переходного процесса, для чего вводится понятие постоянной времени цепи τ : τ - промежуток времени, по истечении которого свободная составляющая уменьшается в е раз ( е = 2,71828…).

Длительность переходного процесса обычно считают равной (3 ÷ 4) τ. По истечении этого промежутка времени остаточное значение свободной составляющей равно сотым долям ее начального значения.

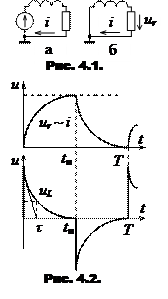Для цепей первого порядка (с одним накопителем) 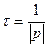. В цепях с большим числом накопителей длительность переходного процесса оценивается по наиболее медленно затухающей свободной составляющей. Если корни характеристического уравнения имеют вид

p_1,2 = - δ ± јω ,

постоянная времени определяется по формуле .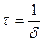

Рассмотрим особенности переходных процессов в цепях первого и второго порядка. Наиболее наглядно переходные процессы можно изучать при подключении цепи к постоянному источнику. Так как в этом случае вынужденная составляющая имеет постоянное значение, свободная составляющая может быть выделена в чистом виде и наблюдаться на экране осциллографа.

В лабораторной установке для изучения переходных процессов используется генератор импульсов прямоугольной формы, при этом длительность импульса (паузы) выбирается такой, чтобы она была сравнима с постоянной времени переходного процесса.

Период повторения импульсов Т = 1/f , где f - частота задающего генератора. Так как длительность импульсов t_и равна длительности пауз между ними, t_и = 1 / 2f.

Расчетная схема замещения, например, для цепи r-L, в интервале действия импульса изображена на рис.4.1а и соответствует включению цепи r-L к источнику постоянной ЭДС, а в интервале паузы – на рис.4.1.б (короткое замыкание цепи r-L). Типовые осциллограммы этого эксперимента приведены на рис.4.2.

Поскольку на активном сопротивлении r напряжение и ток связаны прямой пропорциональной зависимостью u_r = i·r, кривая напряжения u_r(t) в соответствующем масштабе является и кривой тока в цепи i(t).

Из осциллограммы нетрудно определить постоянную времени τ. Она равна отрезку подкасательной, построенной в соответствии с рис.4.2. Для цепи r-L постоянная времени равна L/r, для цепи r-С - величине rC. Более точно можно по осциллограмме определить постоянную времени исходя из того, что , как уже было отмечено , за время τ свободная составляющая уменьшается в е = 2,72 раза и составляет приблизительно 0,37 от ее максимального значения (рис.4.2.). В любом случае предварительно необходимо определить масштаб времени для данной осциллограммы (величина Т=1/f известна).

Более сложный характер имеют переходные процессы в цепях с двумя реактивными элементами. В этом случае в зависимости от корней характеристического уравнения они являются либо апериодическими, либо колебательными. Например, для случая последовательного соединения элементов, если выполняется соотношение r > 2 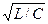, процесс носит апериодический характер. При обратном неравенстве r < 2 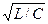процесс колебательный. Режим, при котором r = 2 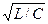, носит название критического.

При колебательном процессе величина r/2L характеризует быстроту затухания процесса, при этом постоянная затухания τ = 2L / r. Частота возникающих при этом колебаний, определяется из соотношения 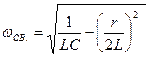, носит название частоты свободных колебаний. Если затухание в системе невелико, т.е. 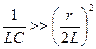, то

ω_СВ. ≈ ω₀ = 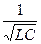, где ω₀ - резонансная частота контура. В этом случае колебания затухают медленно и для их оценки вводят понятие декремента затухания, определяемого отношением амплитуд, измеряемых через промежуток времени, равный периоду колебаний, Δ = е ^-δΤ.

2. Предварительная подготовка

Студенты, пропустившие лаб. работы №1, №2, №3 и не знающие номер своего стенда, выполняют предварительный расчет для произвольно взятого стенда.

Студенты, записавшиеся на отработку, выполняют предварительный расчет для

произвольно взятого стенда.

2.1. Для п.п. 3.1 – 3.3 нарисовать в отчете схемы экспериментов.

Таблица 4.1.

2.2. Рассчитать значения активных сопротивлений для п.п. 3.1 и 3.2. (табл. 4.1.).

2.3. Для п. 3.3 рассчитать значение r_КР.

	ст.№1	ст.№2	ст.№ 3	ст.№ 4	ст.№ 5	ст.№ 6	ст.№ 7	ст.№ 8	ст.№ 9	ст.№10
LB , мГн	26,6	28,0	29,3	29,5	28,4	28,3	28,2	27,5	30,5	28,4
CH , мкФ	0,2233	0,2609	0,2285	0,2235	0,2203	0,2241	0,2517	0,2225	0,2438	0,2311
CB, пФ

1 мГн = 10^-3 Гн, 1 мкФ = 10^-6 Ф, 1 пФ = 10^-12 Ф

3. Задание на проведение эксперимента

(напряжение на генераторе считать однополярным, u_ВХ.≥0)

3.1. Включить «СЕТЬ», «ГЕНЕРАТОР», «КОММУТАТОР ОСЦИЛЛОГРАФ». Вольтметр

и фазометр не включать.

Переключатели на первом канале и входе «Х» перевести в положение «ВНУТР»,

«КАНАЛ» - в среднее положение.

Собрать схему последовательного соединения L_B и R_М.