Вычислить определённый интеграл .
Задание 4
Вычислить площадь фигуры, ограниченной линиями:
xy = 3, y + x = 4.
Задание 5
По формулам трапеций и парабол (Симпсона) приближенно вычислить интеграл 
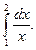
Сведения из теории
Таблица интегралов
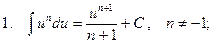
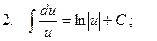
3. 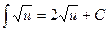 ;
;
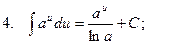
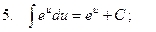
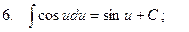
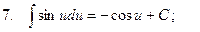
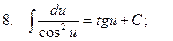
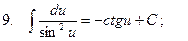
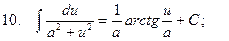
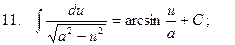
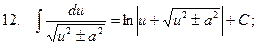
Свойства неопределённого интеграла
1. 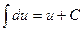 ;
;
2. 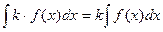 , k – число;
, k – число;
3. 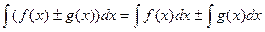 .
.
Метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводится к табличному интегралу, называется непосредственным интегрированием.
При сведении интегралов к табличным, используются следующие свойства дифференциала:
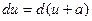 , a – число,
, a – число,
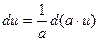 , a
, a 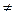 0 – число, а также преобразования:
0 – число, а также преобразования:
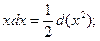
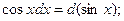
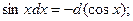
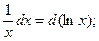
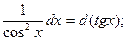
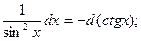
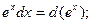
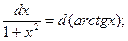
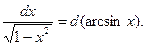
Пример выполнения задания 1
Непосредственным интегрированием найдём следующие интегралы:
а) 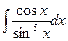 ; б)
; б) 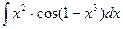 ;
;
в) 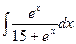 ; г)
; г) 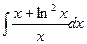 .
.
Сведем данные интегралы к табличным.
а) 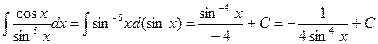 .
.
б) 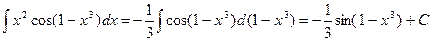 .
.
в) 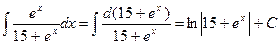 .
.
г)
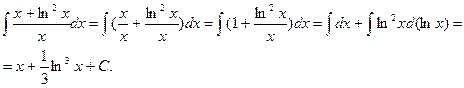
Пример выполнения задания 2
Проинтегрируем, выбрав нужный метод интегрирования.
а) 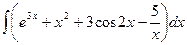 ;
;
б) 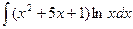 ;
;
в) 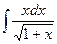 ;
;
Г) .
Решение.
а) 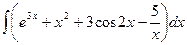 .
.
Используя метод непосредственного интегрирования и свойства неопределённого интеграла, заданный интеграл преобразуем к сумме табличных интегралов.
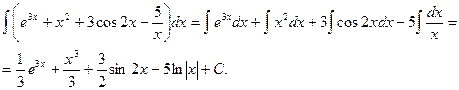
б) 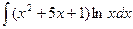 .
.
Применим метод интегрирования по частям:
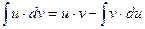 .
.
Обозначим: 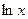 =
= 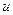 ,
, 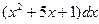 =
= 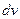 , найдем
, найдем 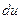 и
и 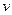 и подставим полученные выражения в формулу интегрирования по частям:
и подставим полученные выражения в формулу интегрирования по частям:
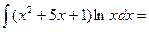
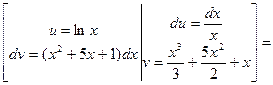
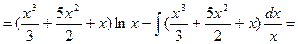
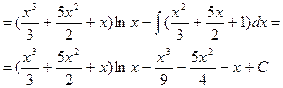 .
.
в) 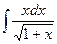 .
.
Применим метод замены переменной, обозначив 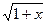 за переменную
за переменную 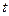 .
.
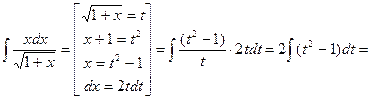
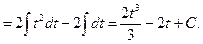
Вернёмся к переменной х:
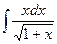
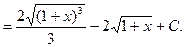
г) 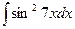 .
.
Применим формулу понижения степени синуса: 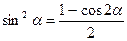 .
.
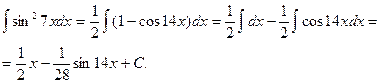
Пример выполнения задания 3
Вычислим определенный интеграл 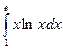 .
.
Решение.
Применим метод интегрирования по частям в определённом интеграле.

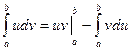 .
.

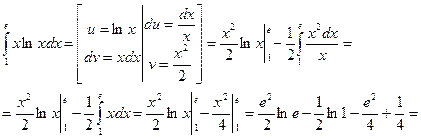


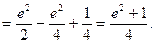


Ответ: 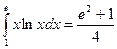 .
.
Пример выполнения задания 4
Вычислим площадь фигуры, ограниченной следующими линиями:
xy = 3, y + x = 4.
Решение.
Строим в прямоугольной системе координат данные линии.


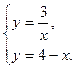
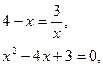
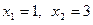 .
.
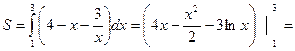 =4 – 3 ln3 (ед2).
=4 – 3 ln3 (ед2).
Ответ: S = 4 – 3 ln 3 (ед2).
Пример выполнения задания 5
По формулам трапеций и парабол (Симпсона) приближённо вычислим интеграл 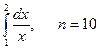 .
.
Решение.
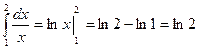 – точное значение интеграла.
– точное значение интеграла.
Применим формулу трапеций:
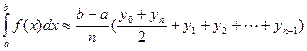 ,
,
В нашей задаче 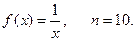
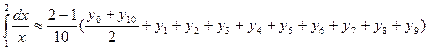 .
.
Составим таблицу значений:
| х |  | х |  |
| х0=1,0 | у0=1,00000 | х6=1,6 | у6=0,62500 |
| х1=1,1 | у1=0,90909 | х7=1,7 | у7=0,58824 |
| х2=1,2 | у2=0,83333 | х8=1,8 | у8=0,55556 |
| х3=1,3 | у3=0,76923 | х9=1,9 | у9=0,52632 |
| х4=1,4 | у4=0,71429 | х10=2,0 | у10=0,50000 |
| х5=1,5 | у5=0,66667 |
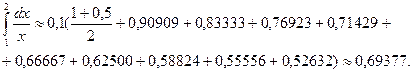
Применим формулу Симпсона:
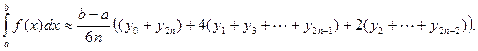
Сравнивая приближённые значения интеграла со значением, полученным по формуле Ньютона-Лейбница, 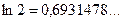 , мы видим, что формула Симпсона дает более точный результат, чем формула трапеций.
, мы видим, что формула Симпсона дает более точный результат, чем формула трапеций.
Модуль 6
Интегральное исчисление функций нескольких переменных
Задачи для решения
Задание 1
Вычислить двойной интеграл по области интегрирования D.
Варианты
1. 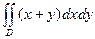 , где область D ограничена линиями
, где область D ограничена линиями
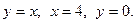
2. 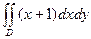 , где область D ограничена линиями
, где область D ограничена линиями
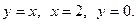
3. 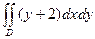 , где область D ограничена линиями
, где область D ограничена линиями
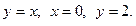
4. 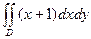 , где область D ограничена линиями
, где область D ограничена линиями
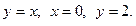
5. 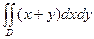 , где область D ограничена линиями
, где область D ограничена линиями
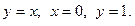
6. 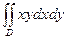 , где область D ограничена линиями
, где область D ограничена линиями
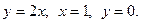
7. 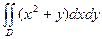 , где область D ограничена линиями
, где область D ограничена линиями
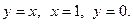
8. 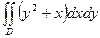 , где область D ограничена линиями
, где область D ограничена линиями
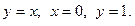
9. 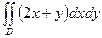 , где область D ограничена линиями
, где область D ограничена линиями
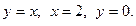
10.  , где область D ограничена линиями
, где область D ограничена линиями
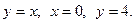
Задание 2
С помощью двойного интеграла вычислить площадь фигуры, ограниченной данными линиями.
Варианты.
1. х2+ у2 ≥ 1, х2 + у2 ≤ 4;
2. х2+ у2≥ 1, х2+ у2≤ 4; х ≥ 0, у ≥ 0;
3. х2+ у2 ≥ 1, х2 + у2≤ 9;
4. х2+ у2 ≥ 1, х2+ у2 ≤ 9; х ≥ 0, у ≥ 0;
5. х2+ у2 ≥ 4, х2+ у2 ≤ 9;
6. х2+ у2 ≥ 4, х2+ у2 ≤ 9; х ≥ 0, у ≥ 0;
7. х2+ у2 ≥ 9; х2+ у2 ≤ 16;
8. х2+ у2 ≥ 9, х2+ у2 ≤ 16; х ≥ 0, у ≥ 0;
9. х2+ у2 ≥ 4, х2+ у2 ≤ 16;
10. х2+ у2 ≥ 4, х2+ у2 ≤ 16; х ≥ 0, у ≥ 0.
Задание 3
С помощью тройного интеграла найти объём тела, ограниченного данными поверхностями.
Варианты
1. z = 4 - х2- у2, z =0;
2. z =х2+ у2+ 1, z =5;
3. z = х2+ у2, z = 9;
4. z2= х2+ у2, z = 2;
5. z = х2+ у2, z =4;
6. z = 9 - х2- у2, z =0;
7. z2= х2+ у2, z = 3;
8. z =х2+ у2+ 2, z =6;
9. z = 5 - х2- у2, z =1;
10. z = 7 - х2- у2, z =3;
Решение типовых задач
Задание 1
Вычислить двойной интеграл по области интегрирования D.
а) 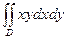 , где область D ограничена линиями
, где область D ограничена линиями
у = х, у = 2, х=0.
б) 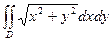 , где область D ограничена линиями:
, где область D ограничена линиями:
х2+ у2 ≥ 1, х2+ у2 ≤ 4, 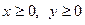 .
.
Задание 2
С помощью двойного интеграла вычислить площадь фигуры, ограниченной линиями:
а) у = х2 + 1, у = х + 3;
б) ρ = 2 sin φ, ρ = 4 sin φ.
Задание 3
С помощью тройного интеграла найти объём тела, ограниченного поверхностями:
а) z = х2+ у2, z = 1.
б) х+ у+ z = 1, х = 0, у = 0, z = 0.
Пример выполнения задания 1
а) Вычислим двойной интеграл 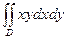 по области интегрирования D, ограниченной линиями у = х, у = 2, х = 0.
по области интегрирования D, ограниченной линиями у = х, у = 2, х = 0.
Решение
Строим область интегрирования D в прямоугольных координатах и расставляем пределы интегрирования в повторном интеграле.

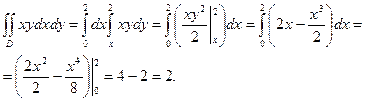
Ответ: 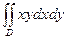 = 2.
= 2.
б) Вычислим интеграл 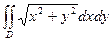 , где область D
, где область D
 ограничена линиями х2+ у2 ≥ 1,
ограничена линиями х2+ у2 ≥ 1,
х2+ у2 ≤ 4, 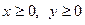 .
.
Строим область интегрирования D.
По области D определяем, что
данный интеграл следует вычислять
в полярных координатах.
Приведём к полярным координатам
уравнение окружности 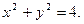
Формулы перехода к полярным координатам: 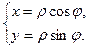
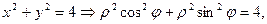
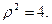
Уравнение окружности 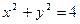 в полярных координатах
в полярных координатах 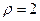 . Аналогично уравнение окружности х2+ у2 = 1 в полярных
. Аналогично уравнение окружности х2+ у2 = 1 в полярных
координатах 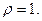
Область Dограничена линиями 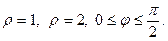
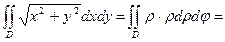
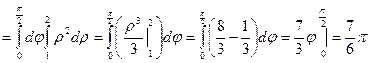 .
.
Ответ: 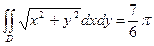 .
.
Пример выполнения задания 2
а) С помощью двойного интеграла вычислим площадь фигуры, ограниченной линиями: у = х2 + 1, у = х + 3.
Решение.
В прямоугольных координатах площадь области D: 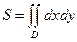
Строим в прямоугольных координатах линии у = х2 +1 и у = х+3.
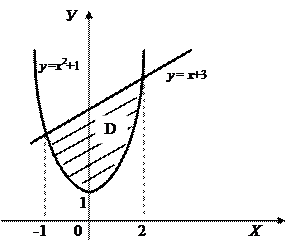 |
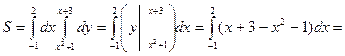
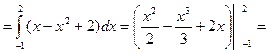
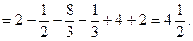
Ответ: 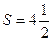 (ед2).
(ед2).
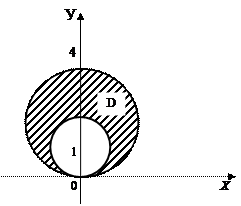
б) С помощью двойного интеграла вычислим площадь фигуры, ограниченной линиями, заданными в полярных координатах:
ρ = 2 sin φ, ρ = 4 sin φ.
Решение.
Линии ρ = 2 sin φ, ρ = 4 sin φ представляют собой окружности диаметров 2 и 4, центры которых лежат в точках (0,1) и (0,2) соответственно. Площадь фигуры, заключённой между этими окружностями вычисляем по формуле:
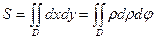
 |

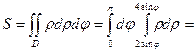
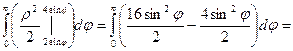
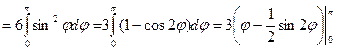
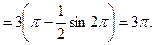
Ответ: 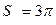 (ед2).
(ед2).
Пример выполнения задания 3
С помощью тройного интеграла найдём объём тела, ограниченного поверхностями z = х2+ у2, z = 1.
Данное тело ограничено плоскостью z = 1 и параболоидом
z = х2+ у2. Найдем объём тела через тройной интеграл, используя цилиндрические координаты.
 |
 |
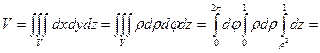
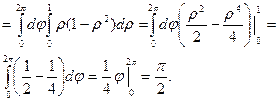
Ответ: 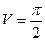 (ед3).
(ед3).
III семестр
Вопросы
1. Обыкновенные дифференциальные уравнения. Основные понятия. Задача Коши.
2. Дифференциальные уравнения первого порядка с разделяющимися переменными.
3. Линейные дифференциальные уравнения первого порядка.
4. Однородные дифференциальные уравнения первого порядка.
5. Уравнения первого порядка в полных дифференциалах.
6. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами.
7. Нахождение общего решения линейного однородного дифференциального уравнения с постоянными коэффициентами по корням его характеристического уравнения
8. Решение линейного неоднородного дифференциального уравнения с постоянными коэффициентами методом неопределенных коэффициентов.
9. Общие сведения о числовых рядах. Абсолютная и условная сходимость числовых рядов.
10. Необходимые признаки сходимости числовых рядов.
11. Достаточные признаки сходимости числовых рядов (признак сравнения, признак Даламбера, радикальный признак Коши, интегральный признак Коши, признак Лейбница).
12. Степенные ряды. Теорема Абеля.
13. Область и радиус сходимости степенного ряда.
14. Общие сведения о тригонометрических рядах и периодических функциях.
15. Ряд Фурье. Достаточное условие разложимости функций в ряд Фурье.
16. Нахождение коэффициентов тригонометрического ряда для функций с периодом 2π.
17. Разложение в ряд Фурье функций с периодом 2l.
18. Разложение функций в ряд Фурье четным и нечетным образом.
Модуль 7
Дифференциальные уравнения
Задачи для решения
Задание 1
Проинтегрировать дифференциальные уравнения. Найти частные решения, удовлетворяющие соответствующим начальным условиям.
Варианты
1. a) 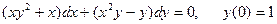 ;
;
б) 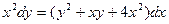 ;
;
в) у' + ycosx = cosx, y(0) = -2;
г) 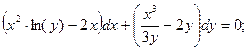
2. а) y' ctgx+ y = 2, y(0) = 1;
б) 2xy' (x2 + y2) = y(y2 + 2x2);
в) xy' - x2sinx = y;
г) (2y – x + 3y2)dy + (3x2 – 2x - y)dx = 0;
3. а) 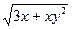 dx+ 2хуdу= 0, y(4) = 1;
dx+ 2хуdу= 0, y(4) = 1;
б) 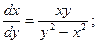
в) 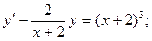
г) 3 x2 (1 + lny)dx – (2y – 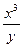 )dy = 0;
)dy = 0;
4. а) y' tgx = ylny, y( 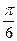 ) = е;
) = е;
б) 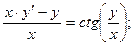
в) 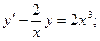
г) (2y - 3)dx + (2x + 3y2)dy = 0;
5. а) (xy +х )dx - (x2+1)dy = 0, y(1) = 0;
б) xy' cos(y/x) = y cos(y/x) – x;
в) y' cosx + ysinx = 1;
г) (2xy + 1)dx + (x2-y2)dy = 0;
6. а) 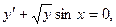
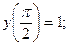
б) 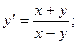
в) y' + y tgx= 2x cosx;
г) 3x2 ey dx + (x3ey + 1)dy = 0;
7. а) xy' – y2 = 1; y(1) = 1;
б) 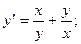
в) y' + 2xy = 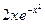 ;
;
г) e-ydx + (2y – xe-y)dy = 0;
8. а) 3ex sinydx – (ex + 1) cosydy = 0, y(0) = π/2;
б) 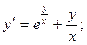
в) 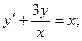
г) (12x + 5y – 9) dx + (5x + 2y – 4) dy = 0;
9. а) xy y' = 1 – x2 , y(1) = 2;
б) 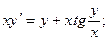
в) 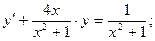
г) (x + lny)dx + (1 + 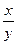 + siny)dy = 0;
+ siny)dy = 0;
10. а) (xy2 + x) dx + (x2y - y)dy = 0, 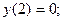
б) x3у' = у(х2 + у2);
в) 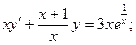
г) 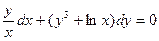 .
.
Задание 2
Найти общее решение линейных дифференциальных уравнений второго порядка с постоянными коэффициентами.
Варианты
1. а) у'' + 7у' + 10 = 0;
б) у'' + 12у' + 36у = 0;
в) 6у'' + 5у' + 2у = 0;
г) у'' + 4у' = 9х + 5;
д) у'' + 8у' + 15у = 2cos3x;
е) у'' + 9у = 5е2х.
2. а) у'' + 5у' + 4у = 0;
б) у'' + 10у' + 25у = 0;
в) 2у'' – 5у' + 6у = 0;
г) у'' + 9у' = 2х + 1;
д) у'' + у = 3е6х;
е) у'' + 2у' – 3у = 4sin5x.
3. а) у'' + 9у' + 18у = 0;
б) у'' – 2у' + у = 0;
в) 3у'' – 5у' + 3у = 0;
г) у'' + 10у' = 6х – 2;
д) у'' + 4у' = 2е5х;
е) у'' + 3у' – 4у = 8 sin2x.
4. а) у'' + 8у' + 7у = 0;
б) у'' – 8у' + 16у = 0;
в) 3у'' + 5у' + 3у = 0;
г) у'' + 4у' = 3х + 5;
д) у'' + 16у' = 3е-4х;
е) у'' + 4у' – 5у = 4cos2x.
5. а) у'' + 10у' + 21у = 0;
б) у'' + 6у' + 9у = 0;
в) 2у'' – 5у' + 4у = 0;
г) у'' + 24у' = 3х – 2;
д) у'' + 25у = 6е7х;
е) у'' – у' – 2у = 5sin6x.
6. а) у'' + 6у' + 8у = 0;
б) у'' + 4у' + 4у = 0;
в) 5у'' – 4у' + у = 0;
г) у'' + 25у' = 9х – 2;
д) у'' + 36у' = 5е4х;
е) у'' + 2у' – 8у = 4cos3x.
7. а) у'' + 8у' + 15у = 0;
б) 3у'' + 6у' + 3у = 0;
в) 3у'' + 4у' + 2у = 0;
г) у'' + 36у' = 8х – 3;
д) у'' + 49у = 7е-3х;
е) у'' + 3у' – 10у = 5cos3x – sin3x.
8. а) у'' +у' – 6у = 0;
б) 9у'' – 6у' + у = 0;
в) у'' + 4у' + 5у = 0;
г) у'' + 49у' = 5х + 4;
д) у'' + 64у = 8е-2х;
е) у'' – у' – 6у = 4sin2x + 3cos2x.
9. а) у'' + 5у' + 6у = 0;
б) у'' 6у' + 9у = 0;
в) у'' + 4у' + 8у = 0;
г) у'' + 8у' = 6х + 2;
д) у'' + 81у = 5е3х ;
е) у'' – 2у' – 3у = 5sin3x.
10. а) у'' + 7у' + 12у = 0;
б) у'' + 8у' + 16у = 0;
в) у'' – 4у' + 20у = 0;
г) у'' +16у' = 2х – 1;
д) у'' + 100у = 4е2х;
е) у'' + у' – 12у = 3cos2x.
Задание 3
Решить систему дифференциальных уравнений.
Варианты
1. 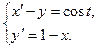 2.
2. 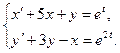
3. 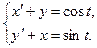 4.
4. 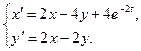
5. 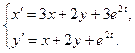 6.
6. 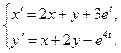
7. 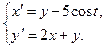 8.
8. 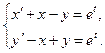
9. 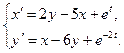 10.
10. 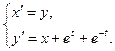
Решение типовых задач
Задание 1
Проинтегрировать дифференциальные уравнения. Найти частные решения, удовлетворяющие соответствующим начальным условиям.
а) х(1 + у2) + у(1 + х2) у' = 0, 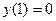 ;
;
б) 2x2dy = (x2 + y2)d;
в) 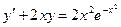 ;
;
г) 2xcos2ydx + (2y – x2sin2у)dy = 0, у(0)=0.
Задание 2
Найти общее решение линейных дифференциальных уравнений.
а) 2y'' + 5у' + 2у = 0;
б) у'' + 6у' + 13у = 0;
в) у'' – 8у' + 16у = 0;
г) у'' – 5у' + 6у = 13sin3x.
Задание 3
Решить систему дифференциальных уравнений
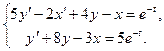
Сведения из теории
Дифференциальные уравнения первого порядка
Дифференциальным называется уравнение, связывающее независимую переменную х, неизвестную функцию у и производную у' или дифференциал неизвестной функции.
По определению дифференциала 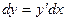 , следовательно,
, следовательно,
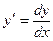 .
.
Общий вид дифференциального уравнения 1-го порядка:
F(x,y,y') = 0, или P(x,y)dx + Q(x,y)dy = 0.
Решением дифференциального уравнения называется всякая функция у = φ(х), которая, будучи подставлена в уравнение, обратит его в тождество, т.е. F(x,φ(x),φ'(x)) = 0.
Задачей Коши для уравнения 1-го порядка называется задача определения частного решения уравнения F(x,y,y') = 0 при заданном начальном условии у(x0) = y0. Существует несколько типов дифференциальных уравнений.
Уравнения с разделяющимися переменными
Если уравнения вида P(x,y)dx + Q(x,y)dy = 0 после преобразования может быть записано в виде
ƒ1(x)ƒ2(y)dx + q1(x)q2(y)dy = 0,
то оно называется уравнением с разделяющимися переменными.
Однородные дифференциальные уравнения
Дифференциальное уравнение, которое можно преобразовать к виду 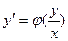 , называется однородным. Подстановка
, называется однородным. Подстановка 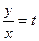 , где
, где 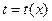 новая неизвестная функция, приводит однородное уравнение к уравнению с разделяющимися переменными.
новая неизвестная функция, приводит однородное уравнение к уравнению с разделяющимися переменными.
Линейные дифференциальные уравнения
Уравнение вида y' + p(x)y = q(x), где p(x) и q(x) непрерывные функции x, называется линейным.
Линейные уравнения решают методом, при котором делается замена 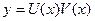 . Одну из двух новых неизвестных функций можно выбирать произвольно. Этой подстановкой линейные уравнения приводятся к двум уравнениям с разделяющимися переменными.
. Одну из двух новых неизвестных функций можно выбирать произвольно. Этой подстановкой линейные уравнения приводятся к двум уравнениям с разделяющимися переменными.
Уравнение в полных дифференциалах
Уравнение P(x,y)dx + Q(x,y)dy = 0 называется уравнением в полных дифференциалах, если его левая часть является полным дифференциалом некоторой функции U(x,y):
P(x,y)dx + Q(x,y)dy = dU(x,y).
Для этого необходимо и достаточно, чтобы выполнялось: 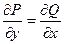 .
.
Пример выполнения задания 1
а) Решим уравнение х(1 + у2) + у(1 + х2) у' = 0 с начальными условиями 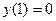 .
.
Решение.
Запишем производную через отношение дифференциалов 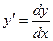 . Получим:
. Получим:
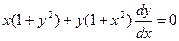 .
.
Представим данное уравнение в виде:
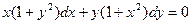 ,
,
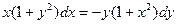 .
.
Разделив обе части этого уравнения на произведение 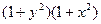 ,
,
получим уравнение с разделяющимися переменными:
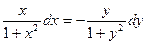 .
.
Интегрируя это уравнение, находим его общее решение:
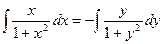 ,
,
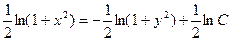 ,
,
(константу С удобно записать в виде 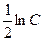 ),
),
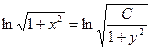 .
.
Получили общее решение дифференциального уравнения:
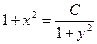 .
.
Найдём частное решение, соответствующее начальным условиям 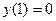 :
:
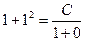 . Отсюда:
. Отсюда: 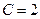 .
.
Частное решение дифференциального уравнения:
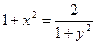 .
.
б) Проинтегрируем однородное уравнение
2x2dy = (x2 + y2)dx.
Решение.
Разделив обе части равенства на x2 , получим:
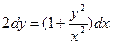 .
.
Положив в нем 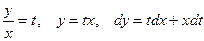 , получим:
, получим: 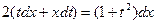 , или
, или 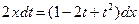 .
.
Это уравнение с разделяющимися переменными.
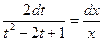 . Интегрируем:
. Интегрируем:
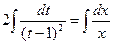
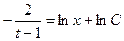 .
.
Возвращаясь к переменной у через обратную замену, получим общий интеграл исходного уравнения:
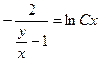 .
.
Эту функцию можно преобразовать к виду: 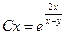 .
.
в) Проинтегрируем линейное уравнение 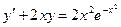 .
.
Решение.
Положим 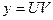 ,
, 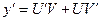 , подставим y и y' в данное
, подставим y и y' в данное
уравнение:
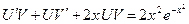 ,
,
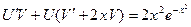 .
.
Положим 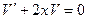 , (*)
, (*)
тогда 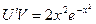 . (**)
. (**)
Решим первое уравнение:
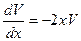 ,
, 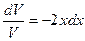 , проинтегрировав, получим:
, проинтегрировав, получим:
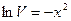 , или
, или 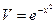 .
.
Подставив V в уравнение (**) , получим:
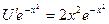 ,
,
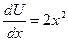 ,
, 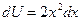 , откуда
, откуда 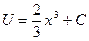 .
.
Общее решение уравнения:
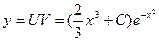 .
.
г) Найдём общее решение дифференциального уравнения 2xcos2ydx + (2y – x2sin2у)dy = 0 и частное решение по данным начальным условиям 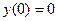 .
.
Решение.
P(x,y) = 2xcos2y , Q(x,y) = 2y – x2sin2y.
Так как 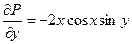 ,
, 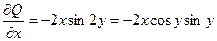 ,
,
из равенства частных производных вытекает, что это – уравнение в полных дифференциалах, т.е. существует такая функция U(x,y), для которой
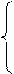
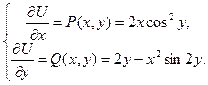
Проинтегрировав первое равенство по х, найдем U(x,y) c точностью до произвольной функции от y:
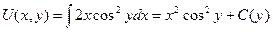 .
.
Чтобы определить С(y), продифференцируем найденную функцию по у:
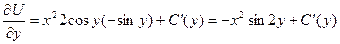 ,
,
приравнивая её к уже известному значению 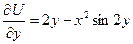 , получим:
, получим: 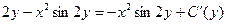 , таким образом,
, таким образом, 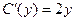 . Проинтегрировав, найдём С(у).
. Проинтегрировав, найдём С(у).
С(y) = y2 + C1.
U(x,y) = x2cos2y +у2 + C1 .
Общий интеграл уравнения: y2 + x2cos2y = C.
Подставив в общий интеграл начальные значения, определим С :
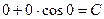 , следовательно, C = 0.
, следовательно, C = 0.
Частное решение исходного уравнения имеет вид:
y2 + x2cos2y = 0.
Сведения из теории
Дифференциальные уравнения высших порядков
