Геометрическая теория деформации

Перемещения и деформации в точке тела. Тензор деформаций. Связь между перемещениями и деформациями (формулы Коши)

Если упругое тело закрепить так, чтобы оно не могло перемещаться как абсолютно твёрдое тело, и приложить внешние нагрузки, то перемещения любой его точки будут вызываться только деформациями этого тела.

Рассмотрим точку M(x, y, z). После деформации тела (рис. 2.5) точка М переместится в новое положение M¢(x¢, y¢, z¢) . Обозначим три компоненты (проекции) вектора перемещения 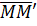на оси координат x, y, z через u, v, w соответственно.

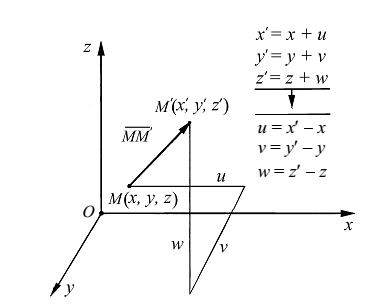
Рисунок 2.5 – К определению понятия «перемещение»

Будем считать, что перемещения тела, по сравнению с его линейными размерами, являются весьма малыми величинами, и, в силу сплошности тела, непрерывно изменяющимися по его объёму. Таким образом, компоненты вектора перемещения являются функциями координат точки:

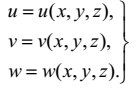(2.13)

Разница в перемещениях в различных точках тела вызывает его деформацию. Деформации обозначаются греческими буквами e и g.

Слайд 14

Рассмотрим элементарный параллелепипед с рёбрами dx, dy, dz вырезанный в окрестности точки P упругого тела до его деформации (рис. 2.6).

Если тело подвергается деформации и величины u, v, w являются компонентами вектора перемещения точки Р, то перемещение в направлении оси x соседней точки A, расположенной на оси x, равно 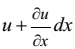, ввиду возрастания функции перемещения u на величину 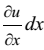с увеличением координаты x на расстояние dx. Увеличение длины ребра PA, т.е. его абсолютное удлинение, вызванное деформацией, равно .

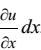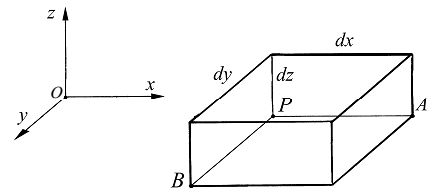
Рисунок 2.6 – Элементарный параллелепипед

Тогда линейная деформация (относительное удлинение) в точке P в направлении x представляет собой отношение абсолютного удлинения ребра PA к его исходной длине dx :

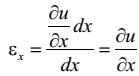
Таким же путём можно показать, что относительные удлинения в точке P в направлениях y и z определяются производными .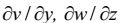

Слайд 15

Рассмотрим изменение угла между элементами PA и PB при деформации параллелепипеда (рис. 2.7).

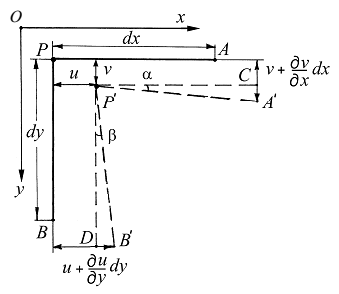
Рисунок 2.7 – К определению угловых деформаций

Пусть точка Р получила перемещения u и v в направлении осей x и y, соответственно. Тогда положение этой точки будет P¢. Перемещение точки A в направлении y будет 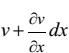, а перемещение точки B в направлении x – 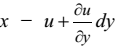В итоге новое направление Р¢А¢ ребра PA образует с начальным направлением малый угол a. Определим его.

Расстояние 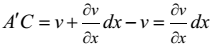Из треугольника DР¢СА находим 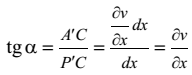Ограничиваясь рассмотрением малых деформаций, можно полагать, что 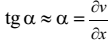Точно так же направление Р¢В¢ повёрнуто к направлению РВ на малый угол b. Аналогично рассуждая, получаем .

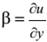Слайд 16

Отсюда видно, что первоначальный прямой угол APB между двумя рёбрами PA и PB уменьшился на величину a +b. Эта величина представляет собой угловуюдеформацию (относительный сдвиг) между направлениями x, y:

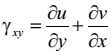
Таким же способом можно получить угловые деформации в плоскостях y, z и x, z. В пределе, когда рёбра параллелепипеда стремятся к нулю, получаем формулы для шести функций деформаций в следующих точках:

– трёх линейных деформаций:

(2.14)

– трёх угловых деформаций:

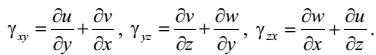(2.15)

Полученные уравнения (2.14) и (2.15) устанавливают связь между функциями перемещений и деформаций. Они называются формулами Коши.

Слайд 17

Если рассматривать «деформированное состояние в точке» как совокупность линейных и угловых деформаций для всевозможных направлений осей, проведённых через данную точку. Тогда тензор деформаций – это совокупность компонент деформации бесконечно малого объёма (в форме параллелепипеда) в окрестности заданной точки:

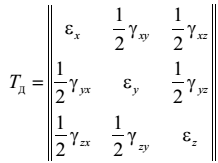(2.16)

Тензор напряжения описывает деформированное состояние в данной точке твёрдого тела.

Относительные удлинения характеризуют изменение длины рёбер параллелепипеда, вырезанного из тела вокруг точки. Индексы указывают направления деформации. Относительные сдвиги характеризуют изменение формы параллелепипеда за счёт искажения его прямых углов. Индексы указывают, в какой координатной плоскости появляется угловая деформация параллелепипеда.

Относительно знаков деформаций существует следующее правило: положительным линейным деформациям e_x, e_y, e_z соответствуют удлинения вдоль осей координат, отрицательным – укорочения; положительным угловым деформациям g_xy, g_yz, g_zx соответствуют уменьшения углов между положительными направлениями осей; отрицательным – увеличения тех же углов.

Слайд 18

Уравнения неразрывности деформаций (уравнения Сен-Венана)

Формулы Коши (2.14), (2.15) связывают шесть компонент тензора деформаций e_x, e_y, e_z , g_xy, g_yz, g_zx и три компоненты вектора перемещения – u, v, w. Если заданы три функции перемещения, то шесть компонент тензора деформаций определяются из формул Коши однозначно. Сложнее обстоит дело с обратной постановкой задачи. Если заданы шесть функций деформаций, то для определения трёх функций перемещений необходимо проинтегрировать шесть дифференциальных уравнений (2.14), (2.15) в частных производных, что не всегда можно сделать однозначно. Поэтому между шестью компонентами тензора деформаций должны существовать определённые зависимости.

Для получения этих зависимостей, которые делятся на две группы, необходимо исключить перемещения u, v, w из формул Коши.

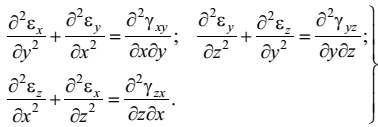(2.17)

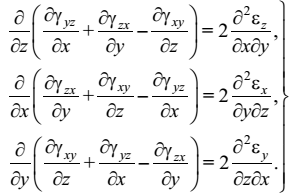(2.18)

Полученные дифференциальные уравнения (1.17), (1.18) называются уравнениями неразрывности деформаций, или уравнениями Сен-Венана.

Геометрическая интерпретация этих соотношений состоит в следующем. Представим себе упругое тело разрезанным на малые параллелепипеды и дадим каждому из них деформацию, определяемую шестью компонентами. Если эти деформации не связаны между собою определёнными зависимостями, то из отдельных деформированных параллелепипедов не удастся вновь сложить непрерывное, но уже деформированное, твёрдое тело: в некоторых точках окажутся бесконечно малые разрывы. Уравнения (1.17) и (1.18) дают такие зависимости между компонентами деформации, при выполнении которых тело после деформации получается сплошным, или непрерывным.