Критерий устойчивости Михайлова

Графический критерий, предложенный в 1938 г. советским ученым А.В. Михайловым, позволяет оценивать устойчивость замкнутой системы на основании годографа функции, полученной по виду характеристического уравнения

.

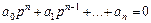Обозначим левую часть этого уравнения через 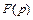и перейдем к частотной переменной, осуществив замену 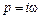. В результате получим комплексную функцию

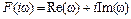, (2.5)

где 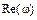– действительная часть, полученная из членов 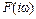, содержащих четные степени ;

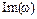– мнимая часть, полученная из членов 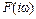с нечетными степенями .

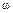Изображение функции (2.5) в комплексной плоскости при изменении частоты 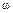в пределах 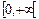носит название годографа Михайлова.

Критерий Михайлова формулируется следующим образом: для устойчивости замкнутой системы n-го порядка необходимо и достаточно, чтобы годограф Михайлова, начинаясь на положительной полуоси, последовательно проходил в положительном направлении (против часовой стрелки) квадрантов комплексной плоскости.

Годограф Михайлова для различных типов систем представлен на рисунке 2.2.

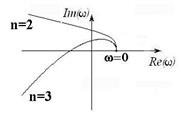
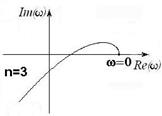
а) устойчивые системы б) неустойчивая система

Рисунок 2.2 – Годограф Михайлова

Условием нахождения системы на границе устойчивости является прохождение годографа Михайлова через начало координат (рису-
нок 2.3).

Следствием из критерия Михайлова является утверждение, что для устойчивости системы необходимо и достаточно, чтобы корни действительной и мнимой 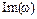частей функции 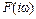чередовались с ростом частоты, начиная с 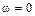, а их общее число было равно порядку системы.

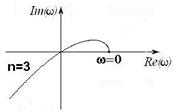
Рисунок 2.3 – Система на границе устойчивости