Табиғи үш жақ. Табиғи өстер. Үдеу векторының жанама және нормаль құраушылары

2.9-сурет

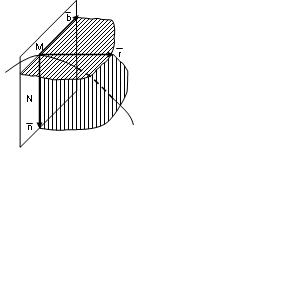
1. Табиғи үш жақ. Табиғи өстер. Траекторияның бір–біріне шексіз жақын орналасқан үш нүктесі арқылы өтетін жазықтық, оның ортаңғы нүктесіне жүргізілген, жанаспа жазықтық деп аталады.

Жанамаға перпендикуляр, М нүктесі арқылы өтетін, N- жазықтығы траекторияның осы нүктедегі нормаль жазықтығы деп аталады.

Траекторияның М нүктесіндегі жанама арқылы өтетін нормаль және жанаспа жазықтықтарға перпендикуляр үшінші жазықтық траекторияның сол нүктедегі түзілеуші жазықтығы деп аталады (2.9-сурет). Жанаспа жазықтықта жатқан нормаль, қисықтың М нүктесіндегі бас нормаль деп, ал жанаспа жазықтыққа осы нүктеде жүргізілген перпендикуляр, бинормаль деп аталады. Жанаманың оң бағыты ( 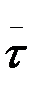бірлік векторы) қозғалыспен бағыттас келеді. Бас нормальдың оң бағыты ( 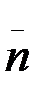бірлік векторы) траекторияның ойыс жағына қарай бағытталады. 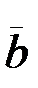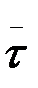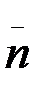Бинормальдың оң бағыты ( бірлік векторы) және векторларымен оң координаттар жүйесін құрайтындай етіп алынады. 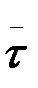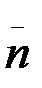Бас нүктесі М болатын бұл координаттар жүйесі М 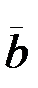табиғи координаттар жүйесі деп, немес табиғи үшжақ деп аталады Координаттар жазықтары екі-екіден алынған бірлік векторларымен анықталады. ( 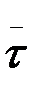, 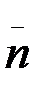) –жанаспа жазықтық, ( 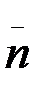, 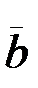) - нормаль жазықтық, ( 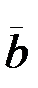, 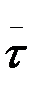) – түзулеуші жазықтық.

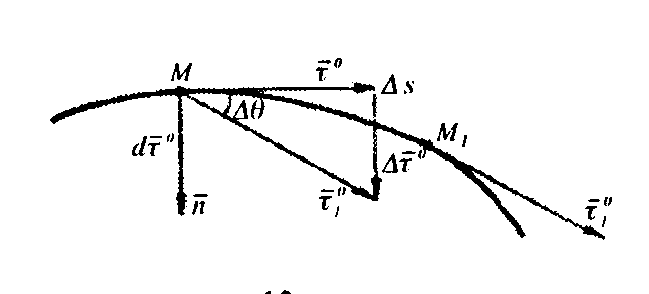
2. Қисық сызық қисықтығы.Нүктенің траекториясын жалпы жағдайда кеңістіктегі қисық сызық деп санаймыз. Нүкте траекториясының М нүктесі берілсін. Траекторияның осы нүктесінде

2.10-сурет

және оған жақын орналасқан екінші нүктесі 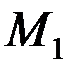арқылы 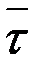және 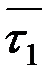жанама бірлік векторларын жүргізейік (2.10-сурет). 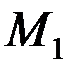нүктесі берілген М нүктесінен 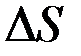қашықтықта болсын, 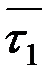векторын М нүктесіне параллель көшірейік. М нүктесіндегі 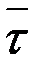және 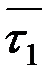екі бірлік векторлар арасындағы бұрышты, 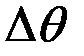деп белгілейік. Бұл бұрыштың 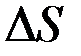доға ұзындығына қатынасын алайық:

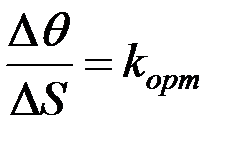. (2.35)

(2.35) қатынасын траекторияның ММ₁ доғасының орташа қисықтығы дейміз. Осы орташа қисықтық ұғымын пайдалана отырып, қисықтық яғни траекторияның берілген нүктедегі қисықтығы деген ұғым енгізе аламыз.

Қисықтың берілген М нүктесіндегі қисықтығы деп орташа қисықтықтың 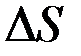нөлге ұмтылғандағы шегіне тең шаманы айтамыз:

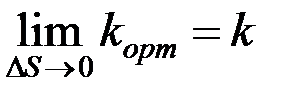. (2.36)

Орташа қисықтық өрнегі (2.35) арқылы (2.36) теңдігін мына түрде жазайық:

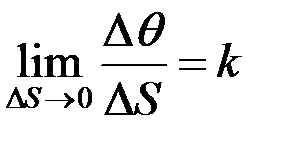. (2.37)

(2.37)-теңдіктің сол жағындағы қатынастың алымының және бөлімінің де шекті мәндерін анықтайық.

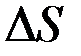нөлге ұмтылғандағы немесе 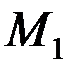нүктесінің траектория бойымен берілген М нүктесіне ұмтылғандағы 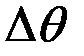бұрыштың шекті мәнін 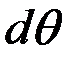деп белгілеп, бұл бұрышты сыбайластық бұрыш деп атаймыз.

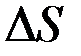-тің 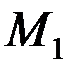нүктесінің траектория бойымен М-ге ұмтылғандағы шегі 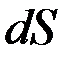доға элементіне тең. Осы түсіндірмелерді пайдалана отырып, (2.37)-анықтаманы былай жазамыз:

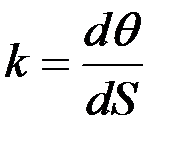. (2.38)

(2.38)-формула қисық сызықтың берілген М нүктесіндегі қисықтығын анықтайды. Ол былай айтылады. Траекторияның берілген нүктесіндегі қисықтығы элементар сыбайластық бұрыштың доға элементіне қатынасына тең шама.

3. Қисықтың берілген нүктедегі қисықтық радиусы.Қисықтың М нүктесі берілсін, оның осы М нүктесіндегі қисықтық радиусы деп осы нүктедегі k –ға кері шаманы айтамыз. Қисықтың берілген М нүктесіндегі қисықтық радиусы 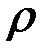десек, онда ол осы айтылған анықтама бойынша мынаған тең:

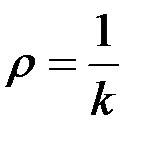. (2.39)

4. Үдеу векторының жанама және нормаль құраушылары.Кеңістікте бойымен М нүктесі қозғалатын қисық берілсін, нүктенің траектория бойындағы М орнына S = 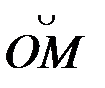доғасы сәйкес келеді. Бұл доғаның t –уақытқа тәуелділігі берілсін:

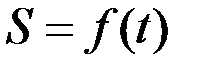(2.40)

2.11-сурет

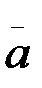Қозғалыс заңы (2.40) теңдігі түрінде берілген М нүктесінің үдеуінің векторы –ны табиғи өстер бағыттарындағы құраушыларға жіктеу керек. Осы мақсатты көздеп жылдамдық векторы 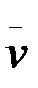-ны жанама бірлік векторы 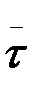арқылы өрнектейік:

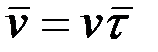(2.41)

мұндағы v, жылдамдық векторы 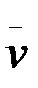-ның 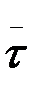бағытындағы проекциясы v_r=v. Егер нүкте қозғалысы доға S-тың ұзындығы есептеудің оң бағытына бағыттас орындалса, онда v_r=v ол егер оның қозғалысы S- ті есептеудің оң бағытына қарсы бағытта өтетін болса , онда v_r= -v .

Екі жағынан уақыт бойынша туынды алу арқылы (2.41)-ді мына түрге келтіреміз:

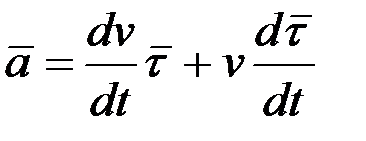(2.42)

Бірлік векторы 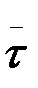-дың дифференциалы, мынаған тең екені белгілі:

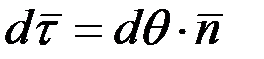(2.43)

Осы (2.43)–теңдікте әрі қарай түрлендірейік:

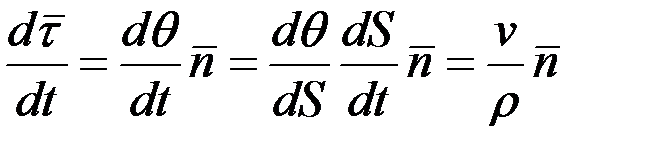(2.44)

мұндағы ρ траекторияның М нүктесіндегі қисықтық радиусы. Соңғы (2.44) теңдікті ескерсек (2.42)–теңдіктен үдеу векторының мынадай жіктелуін аламыз:

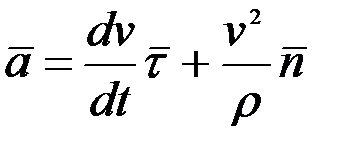(2.45)

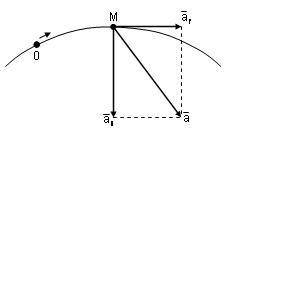
Бұдан, үдеудің жанама және бас нормаль бағыттары бойынша (2.11-сурет), тек екі құраушыға жіктелетінін көреміз. Демек, үдеу векторы жанаспа жазықтықта жатады, сондықтан да оның бинормальдағы құраушысы нөлге тең болады деген қорытындыға келеміз. Олай болса, үдеудің табиғи үшжақ өстеріндегі құраушылары мына түрде беріледі:

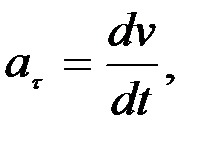
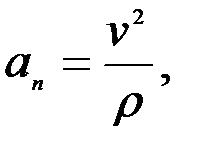
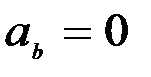(2.46)

Үдеу векторының, 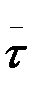бағытындағы құраушысы 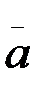_τ= 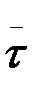dv/dt жанама (тангенцияль) үдеу, ал оның 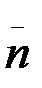-бағытындағы құраушысы 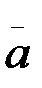_n= 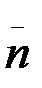v²/ρ нормаль үдеу болады, (2.42) –теңдікті қысқаша мына түрде жазуға да болады (2.11-сурет)

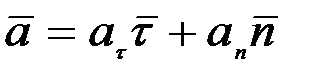(2.47)

Оның модулі:

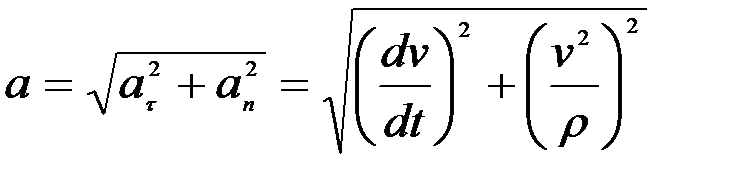(2.48)

Жанама үдеу жылдамдықтың шама жағынан өзгеруін сипаттайды, өйткені ол жылдамдықтың модулінен уақыт бойынша алынған бірінші туындыға тең. Олай болса, нормаль үдеу жылдамдықтың бағытының өзгеруін сипаттауға тиіс. Нормаль үдеудің шамасы әруақытта оң сан болғандықтан, толық 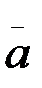үдеу траекторияның қисықтық центріне қарай бағытталғандықтан, оны центрге тартқыш үдеу деп те атайды. Толық үдеудің бағыты, оның бас нормальдың оң бағытымен жасайтын, μ-бұрышымен анықталады (2.11-сурет).

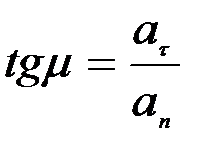(2.49)

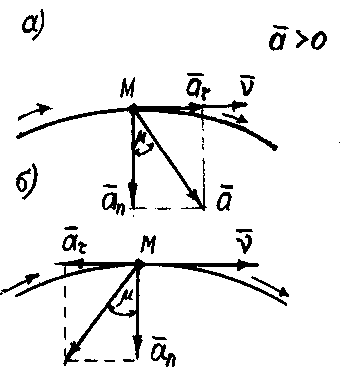
Осы формуладан, жанама үдеу 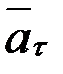-дың таңбасына қарап, яғни жылдамдық модулі v-ның өсуіне не кемуіне байланысты, толық

2.12-сурет 2.13-сурет

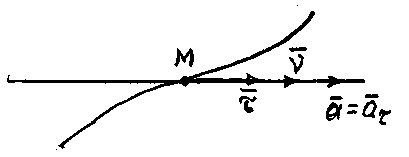
үдеуідің бас нормальдан қозғалыстың бағытына қарай, не оған қарсы бағытқа ауытқитынын көтеміз. Егер 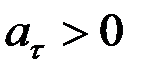(жылдамдықтың шамасы уақыт өткен сайын өсіп отыратын) болса, онда жанама үдеу 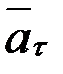де қозғалыстың бағытына қарай бағытталады. Мұндай қозғалыс үдемелі қозғалыс деп аталады (2.12-сурет). Егер 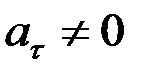болса, онда қозғалыс қисық сызықты қозғалыс, ал 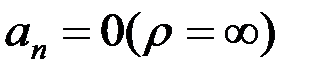болса, онда ол түзу сызықты қозғалыс қозғалыс болады. Тек жеке уақыт кезеңінде ғана 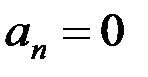болса, онда сол сәтте қозғалушы нүкте траекторияның кері иілу нүктесінде (2.13-сурет) болғаны, не сол сәтте нүктенің жылдамдығы нөлге тең 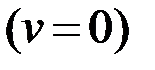болғаны.

Егер 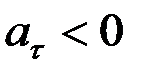(жылдамдық шамасы қозғалыс кезінде кеміп отыратын) болса, 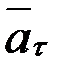және 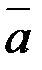векторлары қозғалысқа қарсы бағытталады, ал қозғалыс кемімелі қозғалыс деп аталады (2.12,б-сурет).

Егер барлық уақытта да 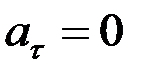жылдамдықтың шамасы тұрақты, яғни 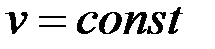болса, қозғалыс бірқалыпты қозғалыс деп аталады. Егер тек қана жеке уақыт кезеңі үшін 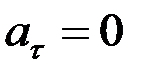болса, онда алгебралық жылдамдық өзінің экстремалды мәнін қабылдағаны. Ал барлық уақытта да 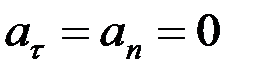болса, онда нүкте бірқалыпты түзу сызықты қозғалыста болғаны.