Высказывания. Элементарные и составные высказывания
Любое рассуждение состоит из цепочки предложений, вытекающих друг из друга по определенным правилам. Среди предложений, в которых идет речь о свойствах или отношениях между математическими понятиями, выделяют высказывания и высказывательные формы (предикаты).
Под высказыванием будем понимать повествовательное предложение, об истинности или ложности которого имеет смысл говорить.
Приведем примеры высказываний:
1) Уфа – столица Башкортостана;
2) В Стерлитамаке зимой никогда нет снега;
3) Нью-Йорк – столица США;
4) 2 > 0;
5) –7 > – 8;
6) 4 + 1 = 5;
7) H2SO4 – кислота;
8) Если число n делится на 4, то оно четное;
9) Неверно, что С.-Петербург – столица России;
10) Пальмы растут в Крыму и на берегу Белого моря;
11) Четырехугольник является параллелограммом тогда и только тогда, когда его диагонали в точке пересечения делятся пополам.
Из определения ясно, что высказываниями не являются вопросительные и восклицательные предложения.
Не являются высказываниями и определения понятий, хотя они имеют форму повествовательного предложения, поскольку представляют собой условное соглашение о введении нового термина.
Предложения, содержащие переменные (х + 2 = 5 и т.д.), тоже не являются высказываниями. Не высказывания и предложения такого типа: «Завтра будет снег», «В субботу я получу оценку 5» и т.д.
Высказывания обозначаются большими латинскими буквами А, В, С и т.д. Каждому высказыванию приписывается значение истинности. Если высказывание А истинно, то записывается А – «И»; если же высказывание А – ложно, то пишут: А – «Л». Любое высказывание может принимать только одно из двух значений истинности.
Высказывания бывают элементарными и составными. Примеры элементарных высказываний среди приведенных выше: 1), 3), 4), 5), 6), 7). Если заданы высказывания А и В, то из них можно составить новые высказывания, используя связки «и», «или», «если ... то», «либо ... либо», «тогда и только тогда», а также частицу «не». Такие высказывания называются составными, а входящие в них высказывания – элементарными. Примеры составных высказываний из приведенных выше: 2), 8), 9), 10), 11).
Два составных высказывания называют равносильными (эквивалентными), если они одновременно «И» или «Л» при любых предположениях об истинности входящих в них элементарных высказываний. В этом случае пишут: А Û В (или А = В).
Операции, выполняемые над высказываниями и порождающие новые высказывания, будем называть логическими операциями.
Приступая к определению логических операций, мы ставим перед собой задачу, чтобы эти определения как можно лучше соответствовали обычному смыслу, в котором употребляются слова «не», «и», «или», «если ... то», «если и только если» в естественном (русском) языке.
Замечание. Синонимами слова «высказывание» являются слова: «суждение», «утверждение», «предложение». Из контекста изложения бывает ясно, почему предпочтение отдано именно этому термину.
Конъюнкция высказываний
Пусть А и В – два элементарных высказывания. Соединив их союзом «и» получим новое высказывание, которое называют конъюнкцией данных высказываний и обозначается А Ù В. Итак, А Ù В читают: «А и В».
Определение. Конъюнкцией двух высказываний А и В называется высказывание 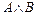 , которое истинно тогда и только тогда, когда истинны оба высказывания А и В.
, которое истинно тогда и только тогда, когда истинны оба высказывания А и В.
Таблица истинности конъюнкции имеет вид (табл. 1):
Таблица 1
| А | B | А Ù В |
| И | И | И |
| Л | И | Л |
| И | Л | Л |
| Л | Л | Л |
П р и м е р. Высказывание «5 – число целое и 6 – число четное» – истинно, так как оба составляющих его элементарных высказывания истинны. Высказывание «2 < 5 и 5 < 10» можно записать так:
2 < 5 < 10. Вообще, двойное числовое неравенство представляет собой конъюнкцию двух числовых неравенств.
Если в А Ù В поменять местами А и В, то получим В Ù А. Составим таблицу истинности (табл. 2).
Таблица 2
| А | B | А Ù В | В Ù А | |
| И | И | И | И | |
| И | Л | Л | Л | |
| Л | И | Л | Л | |
| Л | Л | Л | Л | |
Из таблицы 2 видно, что при разных значениях А и В конъюнкции А Ù В и В Ù А одновременно истинны или ложны. Следовательно, А Ù В = В Ù А. Эта запись означает коммутативное свойство конъюнкции, т.е. высказывания в конъюнкции можно поменять местами.
Составим таблицу истинности для А Ù (В Ù С) и (А Ù В) Ù С (табл. 3).
Таблица 3
| А | B | C | А Ù (В Ù С) | (А Ù В) Ù С |
| И | и | и | и | И |
| Л | и | и | л | Л |
| и | Л | и | л | Л |
| и | и | Л | л | Л |
| Л | Л | и | л | Л |
| Л | и | Л | л | Л |
| и | Л | Л | л | Л |
| Л | Л | Л | л | Л |
Из таблицы 3 видно: при различных значениях А, В и С высказывания 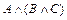 и (А Ù В) Ù С одновременно истинны или ложны. Следовательно, А Ù (В Ù С) = (А Ù В) Ù С. Эта запись означает ассоциативное свойство конъюнкции. Ассоциативность конъюнкции имеет место для трех и более высказываний и позволяет опускать скобки и писать А Ù В Ù С Ù D Ù … .
и (А Ù В) Ù С одновременно истинны или ложны. Следовательно, А Ù (В Ù С) = (А Ù В) Ù С. Эта запись означает ассоциативное свойство конъюнкции. Ассоциативность конъюнкции имеет место для трех и более высказываний и позволяет опускать скобки и писать А Ù В Ù С Ù D Ù … .
Дизъюнкция высказываний
Соединив два элементарных высказывания А и В союзом «или» получим новое высказывание, которое называют дизъюнкцией высказываний и обозначают A Ú B. Итак, A Ú B читают: «A или В».
Определение. Дизъюнкцией двух высказываний А и В называется высказывание 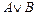 , которое истинно тогда и только тогда, когда истинно хотя бы одно из высказываний А и В.
, которое истинно тогда и только тогда, когда истинно хотя бы одно из высказываний А и В.
Таблица истинности дизъюнкции имеет вид (табл. 4):
Таблица 4
| А | В | A Ú B |
| И | и | и |
| И | л | и |
| л | и | и |
| Л | Л | Л |
По-прежнему употребляем союз «или» в «неразделительном смысле». Если необходимо подчеркнуть разделительный смысл, то употребляют союз «либо, ..., либо». Например: «Завтра в 5 часов я пойду либо в кино, либо к тебе в гости».
Пусть заданы элементарные высказывания «5 > 3», «5 = 3», образуем их дизъюнкцию «5 > 3 или 5 = 3». Она истинна. Короче, высказывание 5 ³ 3 истинно. Вообще, любое нестрогое неравенство представляет собой дизъюнкцию строгого неравенства и равенства.
Например, неравенства 5 £ 5, 10 ³ 8, 18 £ 25 истинны, а неравенства 2 ³ 5, 4 £ 3 ложны.
Для дизъюнкции, как и для конъюнкции, можно указать ряд равносильностей: A Ú B Û B Ú A, A Ú (B Ú C) Û (A Ú B) Ú C – коммутативность и ассоциативность дизъюнкции. Эти равносильности устанавливаются с помощью таблиц истинности (выполните самостоятельно).
Ассоциативность дизъюнкции имеет место для трех и более высказываний и позволяет опускать скобки и писать А Ú В Ú С Ú D и т.д.
Запишем таблицу истинности для (A Ù B) Ú C и (A Ú C) Ù (B Ú C) (табл. 5).
Таблица 5
| А | B | C | (АÙВ)ÚС | (AÚC) | (BÚC) | (AÚC)Ù(BÚC) |
| И | И | И | И | И | И | И |
| И | Л | И | И | И | И | И |
| Л | И | И | И | И | И | И |
| Л | Л | И | И | И | И | И |
| И | И | Л | И | И | И | И |
| И | Л | Л | Л | И | Л | Л |
| Л | И | Л | Л | Л | И | Л |
| Л | Л | Л | Л | Л | Л | Л |
Из таблицы следует вывод: (А Ù В) Ú С = (A Ú C) Ù (B Ú C). Имеет место и такое равенство: (A Ú B) Ù C = (A Ù C) Ú (B Ù C) (проверьте самостоятельно).
Отрицание высказываний
В обыденной речи мы часто пользуемся словом «не» и словами «неверно, что», когда хотим что-то отрицать. Например, если мы хотим отрицать, что «точка X лежит на прямой х», мы говорим «точка X не лежит на прямой х» или «неверно, что точка X лежит на прямой х». Нетрудно заметить, что значения истинности данного высказывания и полученного находятся в определенной связи. Если данное высказывание истинно, то полученное – ложно и наоборот.
Определение.Отрицанием некоторого высказывания А называют такое высказывание, которое истинно, когда А ложно, и ложно, когда А истинно. Обозначают символом 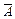 , читается «не А».
, читается «не А».
Из приведенных выше примеров ясно, что отрицание некоторого высказывания А можно получить, если перед данным высказыванием поставить слова «неверно, что» или перед сказуемым поставить частицу «не».
Таблица истинности для 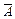 имеет вид (табл. 6):
имеет вид (табл. 6):
Таблица 6
| А | 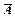 |
| И | Л |
| Л | И |
П р и м е р ы.
1) А – «18 четное число», 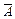 – «18 – не является четным числом».
– «18 – не является четным числом».
2) А – «Иванов не сдал экзамен», 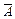 – «Иванов сдал экзамен».
– «Иванов сдал экзамен».
Так как отрицание А есть некоторое высказывание 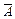 , то можно образовать отрицание высказывания
, то можно образовать отрицание высказывания 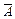 , его обозначают
, его обозначают 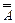 и называют двойным отрицанием высказывания А. Составим таблицу истинности для
и называют двойным отрицанием высказывания А. Составим таблицу истинности для 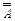 (табл. 7).
(табл. 7).
Таблица 7
| А | 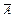 | 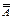 |
| И | Л | И |
| Л | И | Л |
Из таблицы видно, что 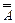 = А.
= А.
П р и м е р: А – «18 – четное число», 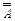 – «18 – не является нечетным числом».
– «18 – не является нечетным числом».
Образуем конъюнкцию высказывания А и 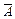 и составим для нее таблицу истинности (табл. 8).
и составим для нее таблицу истинности (табл. 8).
Таблица 8
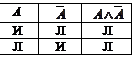 Видим, что формула А Ù
Видим, что формула А Ù 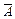 тождественно ложна. Равенство А Ù
тождественно ложна. Равенство А Ù 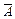 = Л означает, что высказывание вида «А и не А» всегда ложно, какое бы ни было высказывание А.
= Л означает, что высказывание вида «А и не А» всегда ложно, какое бы ни было высказывание А.
Этот закон А Ù 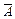 = Л называют законом противоречия.
= Л называют законом противоречия.
Не могут быть одновременно истинными две противоположные мысли об одном и том же предмете, взятом в одно и тоже время и в одном и том же отношении.
Образуем теперь дизъюнкцию некоторого высказывания А и его отрицания 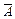 и составим для нее таблицу истинности (табл. 9).
и составим для нее таблицу истинности (табл. 9).
Таблица 9
| А | 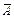 | 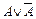 |
| И | Л | И |
| Л | И | И |
В этом случае говорят, что формула А Ú 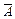 тождественно истинна.
тождественно истинна.
Закон А Ú 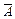 = И называют законом исключенного третьего. Выполняется хотя бы одно из высказываний А или
= И называют законом исключенного третьего. Выполняется хотя бы одно из высказываний А или 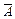 . В математике такая дизъюнкция часто встречается при разборе каких-то взаимоисключающих друг друга случаев.
. В математике такая дизъюнкция часто встречается при разборе каких-то взаимоисключающих друг друга случаев.
Операции конъюнкции, дизъюнкции и отрицания связаны следующими соотношениями, справедливость которых можно установить при помощи таблиц истинности (докажите самостоятельно):
а) 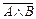 =
= 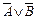 ; б)
; б) 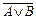 =
= 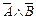 .
.
Эти соотношения называют законами де Моргана.
Импликация высказываний
Рассмотрим составное высказывание, которое образовано из двух элементарных при помощи слов «если ..., то».
Определение. Высказывание «если А, то В» называют импликацией высказываний и обозначают А Þ В. Импликация А Þ В ложна тогда и только тогда, когда А – «И»; В – «Л», в остальных случаях импликация истинна.
Здесь А называют условием импликации, В называют ее заключением.
Таблица истинности для импликации выглядит так (табл. 10).
Таблица 10
| А | В | А Þ B |
| И | И | И |
| И | Л | Л |
| Л | И | И |
| Л | Л | И |
Импликация двух высказываний может быть выражена через отрицание и дизъюнкцию, для любых высказываний А и В:
(A Þ B) Û ( 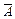 Ú B). Для проверки составим таблицу (табл. 11).
Ú B). Для проверки составим таблицу (табл. 11).
Таблица 11
| А | В | 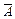 | А Þ В | 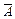 Ú B Ú B |
| И | И | Л | И | И |
| И | Л | Л | Л | Л |
| Л | И | И | И | И |
| Л | Л | И | И | И |
Пусть имеется импликация А Þ В. Из нее можно получить новую импликацию В Þ А, в которой переставлены местами условие и заключение. Эту новую импликацию называют обратной данной. Например, А Þ В: «если число 396 делится на 9, то сумма его цифр делится на 9». А Þ В – «И». Построим обратную импликацию В Þ А: «если сумма цифр числа 396 делится на 9, то и само число делится на 9». В Þ А – «И». Но не всегда обратная импликация для истинной импликации является истинной. Например, данная импликация (А Þ В): «если 25 делится на 10, то 25>10» – «И». Обратная ей импликация (В Þ А): «если 25>10, то 25 делится на 10» – «Л». Из данной импликации А Þ В можно образовать еще две новые импликации. Заменим в данной импликации (А Þ В) условие и заключение их отрицаниями ( 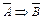 ), получим импликацию противоположную данной. Заменим теперь в данной импликации (А Þ В) условие отрицанием заключения, а заключение отрицанием условия (
), получим импликацию противоположную данной. Заменим теперь в данной импликации (А Þ В) условие отрицанием заключения, а заключение отрицанием условия ( 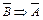 ), получим импликацию противоположную обратной. Докажем с помощью таблиц истинности равносильности А Þ В Û
), получим импликацию противоположную обратной. Докажем с помощью таблиц истинности равносильности А Þ В Û 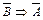 и В Þ А Û
и В Þ А Û 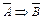 (табл. 12 и 13).
(табл. 12 и 13).

Равносильность А Þ В Û 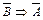 называют законом контрапозиции. Составим отрицание импликации А Þ В, получим:
называют законом контрапозиции. Составим отрицание импликации А Þ В, получим:
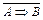 Û
Û 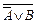 =
= 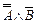 Û
Û 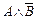 .
.
Это означает следующее: чтобы доказать, что из А не следует В, надо показать, что А истинно, а В ложно.
