Хаотические колебания маятника

Движение частицы в силовых полях, которые периодичны как в пространстве, так и во времени, служит моделью ряда процессов в Физических системах. Среди них классический маятник, заряженная частица в движущемся электрическом поле, синхронные роторы и переход Джозефсона. Например, нелинейная динамика частицы движущейся в бегущем электрическом поле, описывается уравнением

,

где 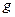– периодическая функция. Изучение вынужденных колебаний маятника, описываемых уравнением

также выявило сложные динамические процессы и хаотические колебания.

Параметрическими колебаниями называют колебания системы при периодических изменениях во времени одного из нескольких параметров системы. Например, стержень на простой подвеске, на который действует осевое доизгибное сжатие, в одномодовом приближении описывается уравнением

.

Это линейное дифференциальное уравнение в обыкновенных производных является хорошо известным уравнением Матье. При определенных значениях и 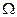это уравнение имеет неустойчивые колебательные решения. Влияние нелинейностей превращает эти колебания в предельный цикл.

Аналогичный пример – маятник с колеблющейся точкой подвеса. Математическое описание такого маятника приводит к уравнению

.

этих численных решениях наблюдаются удвоения периода, и для шестой субгармонической бифуркации оценка числа Фейгенбаума дала .

Рисунок 1.78 - Маятник с параметрическим возбуждением