Платежная матрица. Нижняя и верхняя цена игры

Рассмотрим простейший вид стратегической игры - конечную парную игру. Пусть игрок А располагает m личными стратегиями A_i , (i= 1, 2, ... ,m), а игрок В - n стратегиями В_j , (j= 1, 2, ... , n). Говорят, что игра имеет размерность mxn.

В результате выбора игроками любой пары стратегий

A_i и B_j (i= 1, 2, ... ,m; j= 1, 2, ... , n)

однозначно определяется исход игры, т.е. выигрыш a_ij игрока А (положительный или отрицательный) и проигрыш (-a_ij) игрока В. Выбор стратегий игроками производится при полном незнании выбора другого игрока. Предположим, что значения a_ij известны для любой пары стратегий (A_i,B_j).

Матрица Р=( a_ij), i=1,2,...,m; j=1,2,...,n,элементами которой являются выигрыши, соответствующие стратегиям A_i и B_j, называется платёжной матрицейили матрицей игры:

Р= .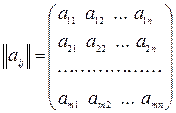

Строки матрицы соответствуют стратегиям A_i игрока А, а столбцы -стратегиям B_j игрока В. Элемент a_ij платёжной матрицы – выигрыш игрока А, если он выбрал конкретную чистую стратегию A_i , а игрок В выбрал конкретную чистую стратегию B_j. Матрица 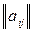задаёт правила платежей (т.е., определяет правила проведения игры).

Пример1. Составить платежную матрицу для игры “поиск”. Игрок А может спрятаться в одном из двух убежищ (I и II). Игрок В ищет игрока А, и если найдет, то получит штраф 1 ден. ед. от А, в противном случае платит игроку А 1 ден. ед.

Решение. Проанализируем поведение каждого игрока.

Стратегия А₁ – А может спрятаться в убежище I, стратегия А₂ - А прячется в убежище II.

Стратегия В₁ – В ищет игрока А в убежище I, стратегия В₂ - В ищет А в убежище II.

Если А находится в убежище I и там его находит В , т.е. осуществляется пара стратегий (А₁,В₁), то А платит штраф, т.е. а₁₁=-1. Аналогично а₂₂=-1 (стратегия (А₂,В₂). Очевидно, стратегии (А₁,В₂) и (А₂,В₁) дают выигрыш 1 игроку А, поэтому а₁₂=а₂₁=1. Т.о. платежная матрица .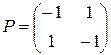

Рассмотрим игру mxn с матрицей Р=( a_ij) i= 1, 2, ... ,m; j= 1, 2, ... , n и определим наилучшую среди стратегий А₁,А₂,…,А_m. Пусть игрок А выбирает некоторую стратегию А_i , тогда в наихудшем случае (например, если выбор игрока А станет известен игроку В) он получит выигрыш, равный 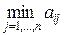. Обозначим через a_i наименьший выигрыш игрока А при выборе им стратегии А_i (наименьшее число в I-ой строке платежной матрицы)_. Т.о. при выборе игроком А некоторой стратегии А_i в наихудшем случае его выигрыш составит a_i = .

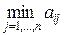Предвидя такую возможность, игрок А должен выбрать такую стратегию, чтобы максимизировать свой минимальный выигрыш, т.е. среди всех чисел a_I (i=1,2,…,m) выбрать наибольшее: 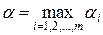. Назовем a нижней ценой игры, или максимальным выигрышем (максимином). Это гарантированный выигрыш игрока А при любой стратегии игрока В.

.

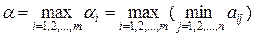Стратегия А_i, соответствующая максимину, также называется максиминной.

Игрок В заинтересован в том, чтобы уменьшить выигрыш игрока А. Выбор стратегии В_j игроком В происходит исходя из принципа, что его проигрыш не превысит максимального из значений элементов j-го столбца матрицы, т.е. £ 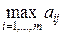. Выбирая стратегию В_j , он учитывает максимально возможный при этом выигрыш для А. Обозначим 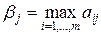. Среди всех чисел b_j, j=1,2,..., n, игрок В выбирает такое значение b_j, при котором минимизируется его максимальный проигрыш, т.е. 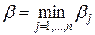, которое назовем верхней ценой игрыили мимнимальным выигрышем (минимаксом). Это гарантированный проигрыш игрока В. Следовательно,

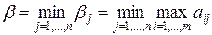
Стратегия В_j, соответствующая минимаксу, называется минимаксной.

Принцип, согласно которому игроки выбирают наиболее “осторожные” минимаксную и максиминную стратегии, называется принципом минимакса. Этот принцип следует из разумного предположения, что каждый игрок стремится достичь цели, противоположной цели противника.

Если верхняя и нижняя цены игры совпадают, то общее значение верхней и нижней цены игры 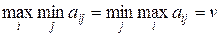(3) называется чистой ценой игры (ценой игры), или значением игры, выигрыш игрока А – вполне определенное число, игра называется вполне определенной.

Минимаксные стратегии, соответствующие цене игры, являются оптимальными стратегиями, а их совокупность – оптимальным решением, или решением игры. В этом случае игрок А получает максимальный гарантированный (не зависящий от поведения игрока В) выигрыш n, а игрок В добивается минимального гарантированного (вне зависимости от поведения игрока А) проигрыша n. Говорят, что решение игры обладает устойчивостью, т.е. если один из игроков придерживается своей оптимальной стратегии, то для другого не может быть выгодным отклоняться от своей оптимальной стратегии.

Вполне определенные игры иногда называют играми с седловой точкой, если элемент 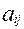, на котором верно равенство a=b=n, является одновременно минимальным в строке i , максимальным с столбце j. Элемент 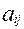называется седловой точкой. Седловой точке соответствуют оптимальные стратегии игроков, их совокупность является решением игры, обладающим свойством устойчивости.

Пример 2. Определить нижнюю и верхнюю цену игры, заданной платежной матрицей

Р = .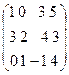

Решение. Минимальные значения a_ij в строках матрицы Рравны соответственно 0, 2, -1. Максимальное значение из них 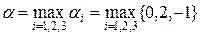=2. Следовательно a=2 – нижняя цена игры, которой соответствует матрица A.

Для определения b (верхней цены данной игры) найдем максимальные значения элементов в столбцах матрицы. По столбцам соответственно имеем: 3, 2, 4, 5. Следовательно, b = min {3; 2; 4; 5} = 2.

Таким образом, a = b = v – цена игры. Решение данной игры состоит в выборе игроком A стратегии A₂, при этом его выигрыш не меньше 2; для игрока B оптимальной является стратегия B₂, позволяющая ограничить его проигрыш этим же числом. Отклонение одним из игроков от оптимальной стратегии приводит к уменьшению выигрыша (для игрока A) и увеличению проигрыша (для игрока B).