Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами
линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами
дифференциальным уравнением первого порядка с разделяющимися переменными
уравнением Бернулли
Решение:
Уравнение 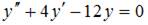 можно представить в виде
можно представить в виде 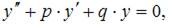 где
где 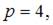
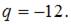 Следовательно, данное уравнение является линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами.
Следовательно, данное уравнение является линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами.
Тема 22: Дифференциальные уравнения с разделяющимися переменными
1. Общий интеграл дифференциального уравнения 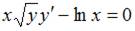 имеет вид …
имеет вид …
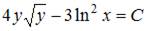 - правильно
- правильно
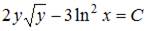
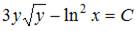
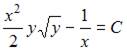
Решение:
Разделим переменные в исходном уравнении: 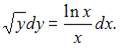 Проинтегрируем обе части уравнения:
Проинтегрируем обе части уравнения: 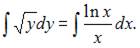 Тогда
Тогда 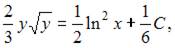
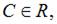 или
или 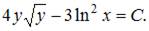
2. Общее решение дифференциального уравнения 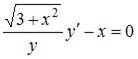 имеет вид …
имеет вид …
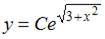 - правильно
- правильно
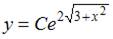
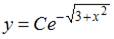
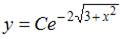
3. Общий интеграл дифференциального уравнения 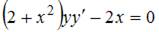 имеет вид …
имеет вид …
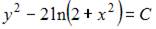 - правильно
- правильно
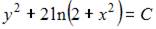
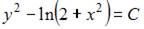
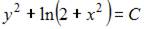
Решение:
Разделим переменные в исходном уравнении: 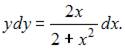 Проинтегрируем обе части уравнения:
Проинтегрируем обе части уравнения: 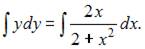 Тогда
Тогда 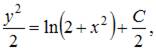 или
или 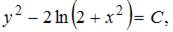 где
где 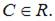
4. Общий интеграл дифференциального уравнения 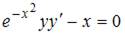 имеет вид …
имеет вид …
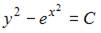 - правильно
- правильно
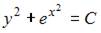
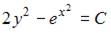
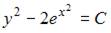
Решение:
Разделим переменные в исходном уравнении: 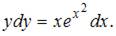 Проинтегрируем обе части уравнения:
Проинтегрируем обе части уравнения: 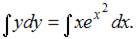 Тогда
Тогда 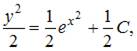
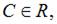 или
или 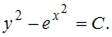
5. Общее решение дифференциального уравнения 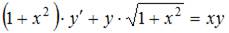 имеет вид …
имеет вид …
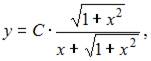
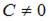 - правильно
- правильно
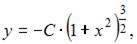
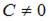
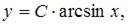
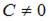
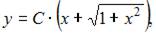
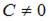
Решение:
Разделим переменные в исходном уравнении: 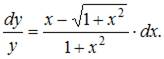
Проинтегрируем обе части уравнения: 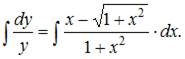 Тогда
Тогда 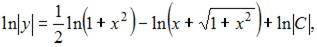 откуда
откуда 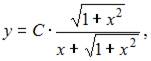 где
где 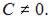
6. Общее решение дифференциального уравнения 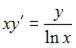 имеет вид …
имеет вид …
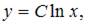
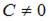 - правильно
- правильно
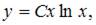
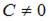
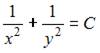
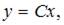
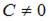
7. Общий интеграл дифференциального уравнения 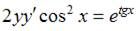 имеет вид …
имеет вид …
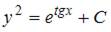 - правильно
- правильно
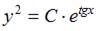
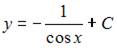
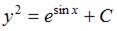
Решение:
Разделим переменные в исходном уравнении: 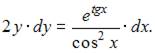
Проинтегрируем обе части уравнения: 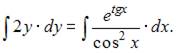 Тогда
Тогда 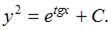
8. Дифференциальное уравнение 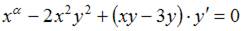 будет уравнением с разделяющимися переменными при значении
будет уравнением с разделяющимися переменными при значении 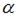 , равном …
, равном …
Решение:
Данное уравнение можно представить в виде: 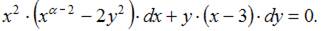
Это уравнение будет уравнением с разделяющимися переменными при 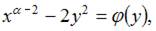 то есть при
то есть при 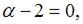 откуда
откуда 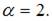
9.Общий интеграл дифференциального уравнения 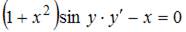 имеет вид …
имеет вид …
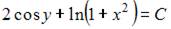 - правильно
- правильно
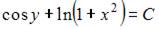
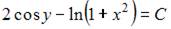
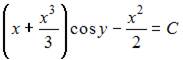
Тема 23: Линейные неоднородные дифференциальные уравнения первого порядка
1. Общее решение дифференциального уравнения 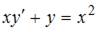 имеет вид …
имеет вид …
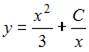 - правильно
- правильно
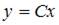
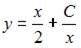
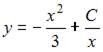
Решение:
Уравнение 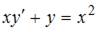 перепишем в виде
перепишем в виде 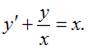 Введем замену
Введем замену 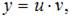
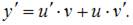 Тогда уравнение
Тогда уравнение 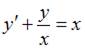 примет вид
примет вид 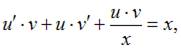 или
или 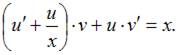
Пусть 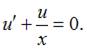 Тогда
Тогда 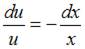 и
и 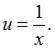 Подставив найденное значение
Подставив найденное значение 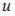 в уравнение
в уравнение 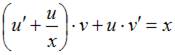 , получим
, получим 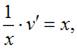
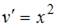 и
и 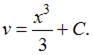 Окончательное решение имеет вид
Окончательное решение имеет вид 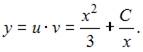
2. Решение задачи Коши 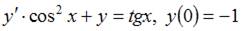 имеет вид …
имеет вид …
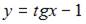 - правильно
- правильно
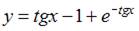
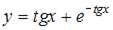
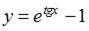
3. Общее решение дифференциального уравнения 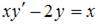 имеет вид …
имеет вид …
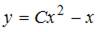 - правильно
- правильно
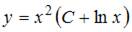
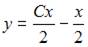
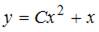
Решение:
Уравнение 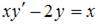 перепишем в виде
перепишем в виде 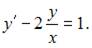 Введем замену
Введем замену 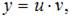
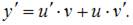 Тогда уравнение
Тогда уравнение 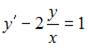 примет вид
примет вид 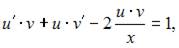 или
или 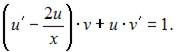
Пусть 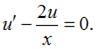 Тогда
Тогда 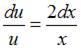 и
и 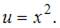 Подставив найденное значение
Подставив найденное значение 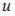 в уравнение
в уравнение 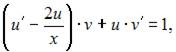 получим
получим 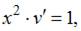
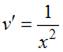 и
и 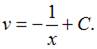 Окончательное решение имеет вид
Окончательное решение имеет вид 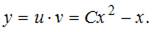
4. Общее решение дифференциального уравнения 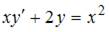 имеет вид …
имеет вид …
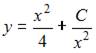 - правильно
- правильно
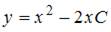
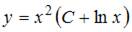
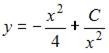
Решение:
Уравнение 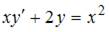 перепишем в виде
перепишем в виде 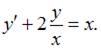 Введем замену
Введем замену 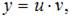
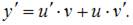 Тогда уравнение
Тогда уравнение 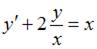 примет вид
примет вид 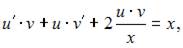 или
или 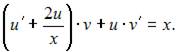
Пусть 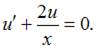 Тогда
Тогда 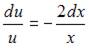 и
и 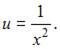 Подставив найденное значение
Подставив найденное значение 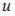 в уравнение
в уравнение 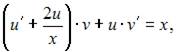 получим:
получим: 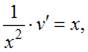
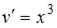 и
и 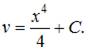
Окончательное решение имеет вид 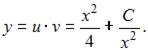
5. Общее решение дифференциального уравнения 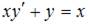 имеет вид …
имеет вид …
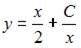 - правильно
- правильно
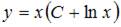
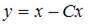
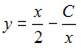
6. Общее решение дифференциального уравнения 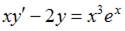 имеет вид …
имеет вид …
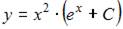 - правильно
- правильно
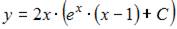
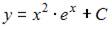
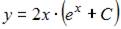
7. Общее решение дифференциального уравнения 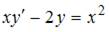 имеет вид …
имеет вид …
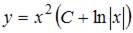 - правильно
- правильно
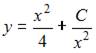
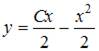
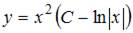
Решение:
Уравнение 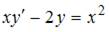 перепишем в виде
перепишем в виде 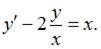 Введем замену
Введем замену 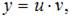
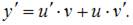 Тогда уравнение
Тогда уравнение 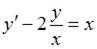 примет вид
примет вид 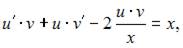 или
или 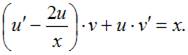
Пусть 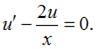 Тогда
Тогда 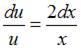 и
и 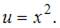 Подставив найденное значение
Подставив найденное значение 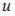 в уравнение
в уравнение 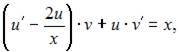 получим
получим 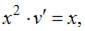
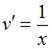 и
и 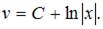 Окончательное решение имеет вид
Окончательное решение имеет вид 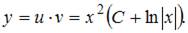
8. Общее решение дифференциального уравнения 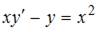 имеет вид …
имеет вид …
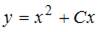 - правильно
- правильно
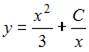
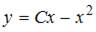
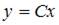
Решение:
Уравнение 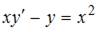 перепишем в виде
перепишем в виде 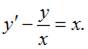 Введем замену
Введем замену 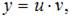
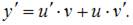 Тогда уравнение
Тогда уравнение 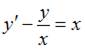 примет вид
примет вид 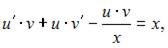 или
или 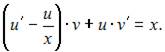
Пусть 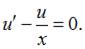 Тогда
Тогда 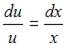 и
и 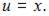 Подставив найденное значение
Подставив найденное значение 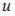 в уравнение
в уравнение 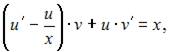 получим
получим 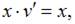
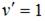 и
и 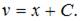 Окончательное решение имеет вид
Окончательное решение имеет вид 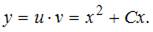
9. Общее решение дифференциального уравнения 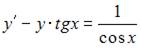 имеет вид …
имеет вид …
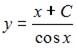 - правильно
- правильно
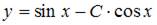
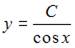
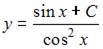
Решение:
Введем замену 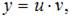
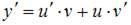 и получим
и получим 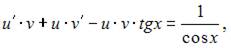 или
или 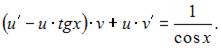
Пусть 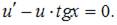 Тогда
Тогда 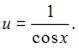 Подставим найденное значение
Подставим найденное значение 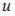 в уравнение
в уравнение 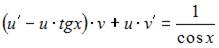 и получим
и получим 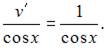 Тогда
Тогда 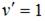 и
и 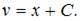
Окончательное решение имеет вид 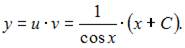
Тема 24: Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
1. Общий вид частного решения 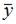 линейного неоднородного дифференциального уравнения второго порядка
линейного неоднородного дифференциального уравнения второго порядка 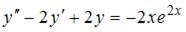 будет выглядеть как …
будет выглядеть как …
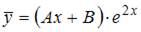 - правильно
- правильно
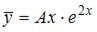
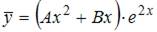
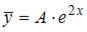
Решение:
Общее решение этого уравнения можно записать в виде 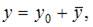 где функция
где функция 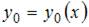 – общее решение однородного уравнения
– общее решение однородного уравнения 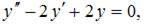 а функция
а функция 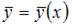 – некоторое частное решение исходного неоднородного уравнения.
– некоторое частное решение исходного неоднородного уравнения.
Для однородного уравнения составим характеристическое уравнение 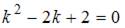 и найдем его корни:
и найдем его корни: 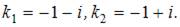 Тогда общее решение однородного уравнения будет иметь вид
Тогда общее решение однородного уравнения будет иметь вид 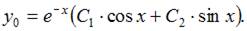
Поскольку правая часть исходного уравнения 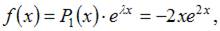 то имеем уравнение со специальной правой частью. Так как
то имеем уравнение со специальной правой частью. Так как 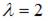 не является корнем характеристического уравнения, то частное решение
не является корнем характеристического уравнения, то частное решение 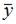 неоднородного уравнения будем искать в виде
неоднородного уравнения будем искать в виде 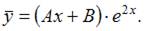
2. Общий вид частного решения 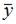 линейного неоднородного дифференциального уравнения второго порядка
линейного неоднородного дифференциального уравнения второго порядка 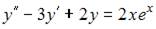 будет выглядеть как …
будет выглядеть как …
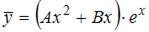 - правильно
- правильно
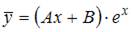
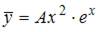
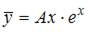
Решение:
Общее решение этого уравнения можно записать в виде 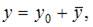 где функция
где функция 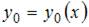 – общее решение однородного уравнения
– общее решение однородного уравнения 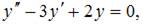 а функция
а функция 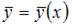 – некоторое частное решение исходного неоднородного уравнения.
– некоторое частное решение исходного неоднородного уравнения.
Для однородного уравнения составим характеристическое уравнение 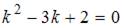 и найдем его корни:
и найдем его корни: 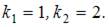 Тогда общее решение однородного уравнения будет иметь вид
Тогда общее решение однородного уравнения будет иметь вид 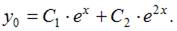
Поскольку правая часть исходного уравнения 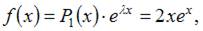 то имеем уравнение со специальной правой частью.
то имеем уравнение со специальной правой частью.
Так как 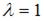 является корнем характеристического уравнения, то частное решение
является корнем характеристического уравнения, то частное решение 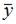 неоднородного уравнения будем искать в виде
неоднородного уравнения будем искать в виде 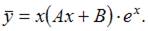
3. Общее решение линейного однородного дифференциального уравнения второго порядка 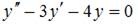 имеет вид …
имеет вид …
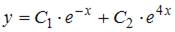 - правильно
- правильно
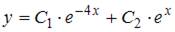
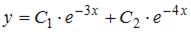
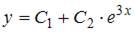
4. Общее решение линейного однородного дифференциального уравнения второго порядка 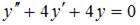 имеет вид …
имеет вид …
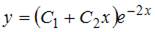 - правильно
- правильно
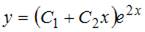
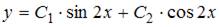
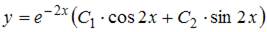
5. Общий вид частного решения 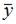 линейного неоднородного дифференциального уравнения второго порядка
линейного неоднородного дифференциального уравнения второго порядка 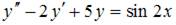 будет выглядеть как …
будет выглядеть как …
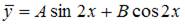 - правильно
- правильно
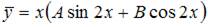
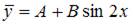
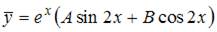
Решение:
Общее решение этого уравнения можно записать в виде 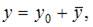 где функция
где функция 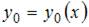 – общее решение однородного уравнения
– общее решение однородного уравнения 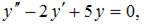 а функция
а функция 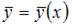 – некоторое частное решение исходного неоднородного уравнения.
– некоторое частное решение исходного неоднородного уравнения.
Для однородного уравнения составим характеристическое уравнение 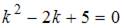 и найдем его корни:
и найдем его корни: 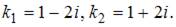 Тогда общее решение однородного уравнения будет иметь вид
Тогда общее решение однородного уравнения будет иметь вид 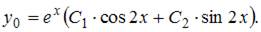
Поскольку правая часть исходного уравнения 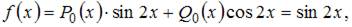 то имеем уравнение со специальной правой частью. Так как
то имеем уравнение со специальной правой частью. Так как 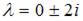 не является корнем характеристического уравнения, то частное решение
не является корнем характеристического уравнения, то частное решение 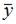 неоднородного уравнения будем искать в виде
неоднородного уравнения будем искать в виде 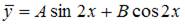 .
.
6. Общее решение линейного однородного дифференциального уравнения второго порядка 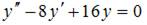 имеет вид …
имеет вид …
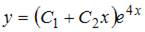 - правильно
- правильно
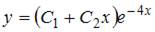
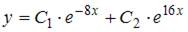
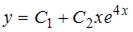
Решение:
Составим характеристическое уравнение 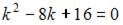 и решим его:
и решим его: 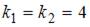 . Тогда общее решение исходного уравнения примет вид
. Тогда общее решение исходного уравнения примет вид 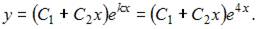
7. Общее решение линейного однородного дифференциального уравнения второго порядка 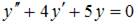 имеет вид …
имеет вид …
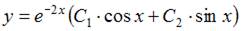 - правильно
- правильно
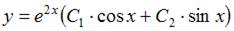
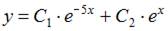
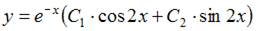
8. Общий вид частного решения 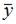 линейного неоднородного дифференциального уравнения второго порядка
линейного неоднородного дифференциального уравнения второго порядка 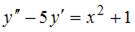 будет выглядеть как …
будет выглядеть как …
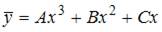 - правильно
- правильно
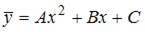
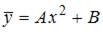
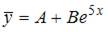
Решение:
Общее решение этого уравнения можно записать в виде 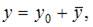 где функция
где функция 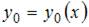 – общее решение однородного уравнения
– общее решение однородного уравнения 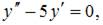 а функция
а функция 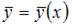 – некоторое частное решение исходного неоднородного уравнения.
– некоторое частное решение исходного неоднородного уравнения.
Для однородного уравнения составим характеристическое уравнение 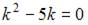 и найдем его корни:
и найдем его корни: 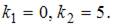 Тогда общее решение однородного уравнения будет иметь вид
Тогда общее решение однородного уравнения будет иметь вид 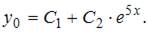
Поскольку правая часть исходного уравнения 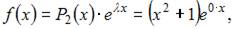 то имеем уравнение со специальной правой частью.
то имеем уравнение со специальной правой частью.
Так как 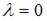 является корнем характеристического уравнения, то частное решение
является корнем характеристического уравнения, то частное решение 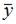 неоднородного уравнения будем искать в виде
неоднородного уравнения будем искать в виде 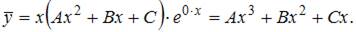
9. Общее решение линейного однородного дифференциального уравнения второго порядка 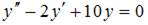 имеет вид …
имеет вид …
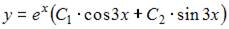 - правильно
- правильно
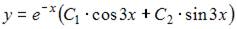
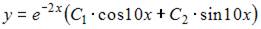
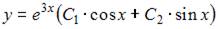
Решение:
Составим характеристическое уравнение 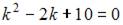 и решим его:
и решим его: 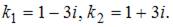 Тогда общее решение исходного уравнения примет вид
Тогда общее решение исходного уравнения примет вид 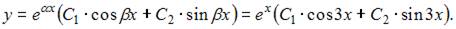
Кейс 1 подзадача 1
1. При доходе потребителя, равном M = 5 у.е., потребление некоторого блага составляет X = 30 ед. Известно, что скорость изменения спроса по доходу равна 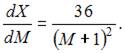
Функция спроса по доходу выражается зависимостью …
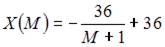 - правильно
- правильно
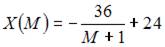
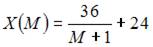
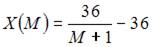
Решение:
Проинтегрируем по t обе части дифференциального уравнения 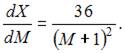 Тогда
Тогда 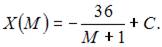 Так как
Так как 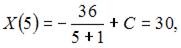 то
то 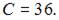
Таким образом, 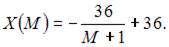
2. При доходе потребителя, равном M = 4 у.е., потребление некоторого блага составляет X = 50 ед. Известно, что скорость изменения спроса по доходу равна 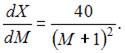
Функция спроса по доходу выражается зависимостью …
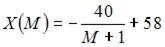 - правильно
- правильно
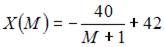
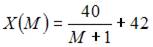
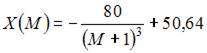
Решение:
Проинтегрируем по t обе части дифференциального уравнения 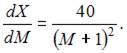 Тогда
Тогда 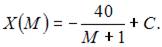 Так как
Так как 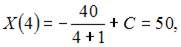 то
то 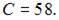
Таким образом, 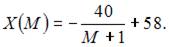
3. При доходе потребителя, равном M = 3 у.е., потребление некоторого блага составляет X = 35 ед. Известно, что скорость изменения спроса по доходу равна 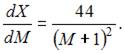
Функция спроса по доходу выражается зависимостью …
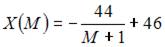 - правильно
- правильно
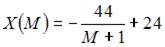
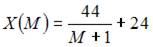
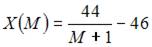
Решение:
Проинтегрируем по t обе части дифференциального уравнения 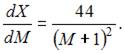 Тогда
Тогда 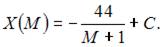 Так как
Так как 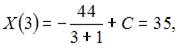 то
то 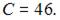
Таким образом, 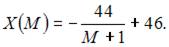
4. При доходе потребителя, равном M = 5 у.е., потребление некоторого блага составляет X = 40 ед. Известно, что скорость изменения спроса по доходу равна 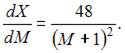
Функция спроса по доходу выражается зависимостью …
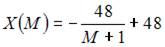 - правильно
- правильно
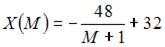
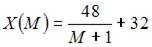
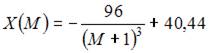
Решение:
Проинтегрируем по t обе части дифференциального уравнения 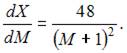 Тогда
Тогда 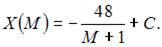 Так как
Так как 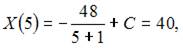 то
то 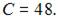
Таким образом, 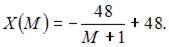
5. При доходе потребителя, равном M = 6 у.е., потребление некоторого блага составляет X = 45 ед. Известно, что скорость изменения спроса по доходу равна 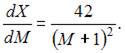
Функция спроса по доходу выражается зависимостью …
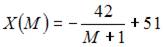 - правильно
- правильно
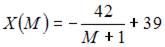
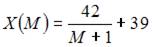
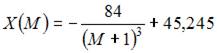
Решение:
Проинтегрируем по t обе части дифференциального уравнения 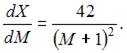 Тогда
Тогда 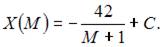 Так как
Так как 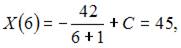 то
то 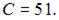
Таким образом, 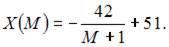
Кейс 1 подзадача 2
1. При доходе потребителя, равном M = 5 у.е., потребление некоторого блага составляет X = 30 ед. Известно, что скорость изменения спроса по доходу равна 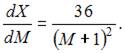
Объем спроса при M = 11 равен …
Решение:
Вычислим 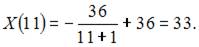
2. При доходе потребителя, равном M = 4 у.е., потребление некоторого блага составляет X = 50 ед. Известно, что скорость изменения спроса по доходу равна 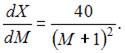
Объем спроса при M = 9 равен …
Решение:
Вычислим 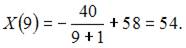
3. При доходе потребителя, равном M = 3 у.е., потребление некоторого блага составляет X = 35 ед. Известно, что скорость изменения спроса по доходу равна 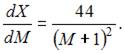
Объем спроса при M = 10 равен …
Решение:
Вычислим 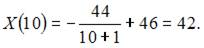
4. При доходе потребителя, равном M = 5 у.е., потребление некоторого блага составляет X = 40 ед. Известно, что скорость изменения спроса по доходу равна 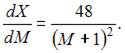
Объем спроса при M = 11 равен …
Решение:
Вычислим 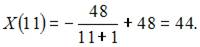
5. При доходе потребителя, равном M = 6 у.е., потребление некоторого блага составляет X = 45 ед. Известно, что скорость изменения спроса по доходу равна 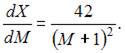
Объем спроса при M = 5 равен …
Решение:
Вычислим 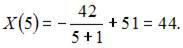
Кейс 1 подзадача 3
1. При доходе потребителя, равном M = 5 у.е., потребление некоторого блага составляет X = 30 ед. Известно, что скорость изменения спроса по доходу равна 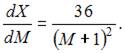
Наибольшее значение объема потребления не превзойдет величины …
Решение:
Функция 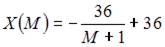 является возрастающей и
является возрастающей и 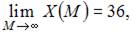 то есть существует горизонтальная асимптота
то есть существует горизонтальная асимптота 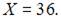 Следовательно, наибольшее значение объема потребления не превзойдет величин
Следовательно, наибольшее значение объема потребления не превзойдет величин 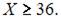
2. При доходе потребителя, равном M = 4 у.е., потребление некоторого блага составляет X = 50 ед. Известно, что скорость изменения спроса по доходу равна 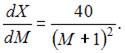
Наибольшее значение объема потребления не превзойдет величины …
Решение:
Функция 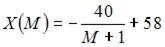 является возрастающей и
является возрастающей и 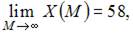 то есть существует горизонтальная асимптота
то есть существует горизонтальная асимптота 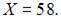 Следовательно, наибольшее значение объема потребления не превзойдет величин
Следовательно, наибольшее значение объема потребления не превзойдет величин 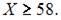
3. При доходе потребителя, равном M = 3 у.е., потребление некоторого блага составляет X = 35 ед. Известно, что скорость изменения спроса по доходу равна 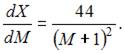
Наибольшее значение объема потребления не превзойдет величины …
Решение:
Функция 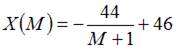 является возрастающей и
является возрастающей и 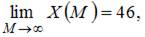 то есть существует горизонтальная асимптота
то есть существует горизонтальная асимптота 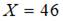 . Следовательно, наибольшее значение объема потребления не превзойдет величин
. Следовательно, наибольшее значение объема потребления не превзойдет величин 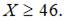
4. При доходе потребителя, равном M = 5 у.е., потребление некоторого блага составляет X = 40 ед. Известно, что скорость изменения спроса по доходу равна 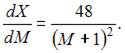
Наибольшее значение объема потребления не превзойдет величины …
Решение:
Функция 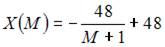 является возрастающей и
является возрастающей и 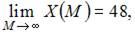 то есть существует горизонтальная асимптота
то есть существует горизонтальная асимптота 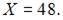 Следовательно, наибольшее значение объема потребления не превзойдет величин
Следовательно, наибольшее значение объема потребления не превзойдет величин 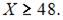
5. При доходе потребителя, равном M = 6 у.е., потребление некоторого блага составляет X = 45 ед. Известно, что скорость изменения спроса по доходу равна 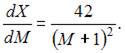
Наибольшее значение объема потребления не превзойдет величины …
Решение:
Функция 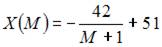 является возрастающей и
является возрастающей и 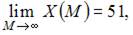 то есть существует горизонтальная асимптота
то есть существует горизонтальная асимптота 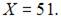 Следовательно, наибольшее значение объема потребления не превзойдет величин
Следовательно, наибольшее значение объема потребления не превзойдет величин 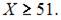
Кейс 2 подзадача 1
1. В процессе производства используются два вида ресурсов: капитал K и труд L. Функция выпуска имеет вид 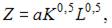 на аренду фондов (капитала) и оплату труда выделено 90 у.е., стоимость аренды единицы фондов равна 3 у.е., ставка заработной платы 5 у.е.
на аренду фондов (капитала) и оплату труда выделено 90 у.е., стоимость аренды единицы фондов равна 3 у.е., ставка заработной платы 5 у.е.
При решении задачи на максимизацию объема выпуска функция Лагранжа имеет вид …
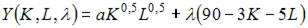 - правильно
- правильно
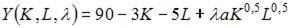
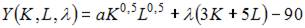
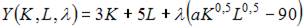
Решение:
Задача максимизации объема производства представляет собой задачу на условный экстремум, в которой 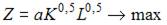 при условии, что
при условии, что 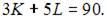
Так как при решении задачи на условный экстремум вида
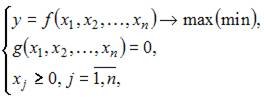
функция Лагранжа имеет вид
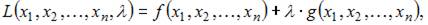
то в нашем случае можно использовать следующую функцию Лагранжа:
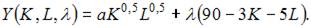
2. В процессе производства используются два вида ресурсов: капитал K и труд L. Функция выпуска имеет вид 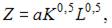 на аренду фондов (капитала) и оплату труда выделено 60 у.е., стоимость аренды единицы фондов равна 3 у.е., ставка заработной платы 4 у.е.
на аренду фондов (капитала) и оплату труда выделено 60 у.е., стоимость аренды единицы фондов равна 3 у.е., ставка заработной платы 4 у.е.
При решении задачи на максимизацию объема выпуска функция Лагранжа имеет вид …
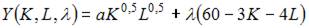 - правильно
- правильно
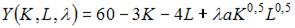
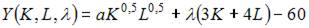
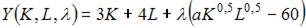
Решение:
Задача максимизации объема производства представляет собой задачу на условный экстремум, в которой 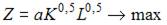 при условии, что
при условии, что 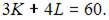
Так как при решении задачи на условный экстремум вида
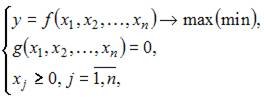
функция Лагранжа имеет вид
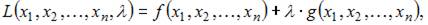
то в нашем случае можно использовать следующую функцию Лагранжа:
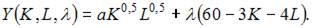
3. В процессе производства используются два вида ресурсов: капитал K и труд L. Функция выпуска имеет вид 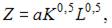 на аренду фондов (капитала) и оплату труда выделено 80 у.е., стоимость аренды единицы фондов равна 4 у.е., ставка заработной платы 5 у.е.
на аренду фондов (капитала) и оплату труда выделено 80 у.е., стоимость аренды единицы фондов равна 4 у.е., ставка заработной платы 5 у.е.
При решении задачи на максимизацию объема выпуска функция Лагранжа имеет вид …
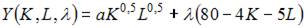 - правильно
- правильно
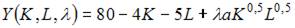
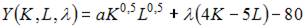
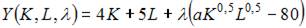
Решение:
Задача максимизации объема производства представляет собой задачу на условный экстремум, в которой 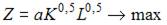 при условии, что
при условии, что 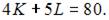
Так как при решении задачи на условный экстремум вида
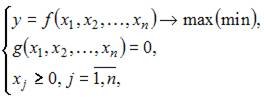
функция Лагранжа имеет вид
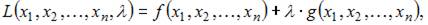
то в нашем случае можно использовать следующую функцию Лагранжа:
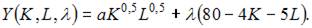
4. В процессе производства используются два вида ресурсов: капитал K и труд L. Функция выпуска имеет вид 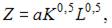 на аренду фондов (капитала) и оплату труда выделено 60 у.е., стоимость аренды единицы фондов равна 5 у.е., ставка заработной платы 3 у.е.
на аренду фондов (капитала) и оплату труда выделено 60 у.е., стоимость аренды единицы фондов равна 5 у.е., ставка заработной платы 3 у.е.
При решении задачи на максимизацию объема выпуска функция Лагранжа имеет вид …
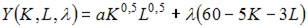 - правильно
- правильно
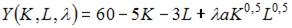
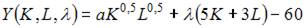
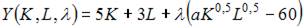
Решение:
Задача максимизации объема производства представляет собой задачу на условный экстремум, в которой 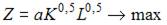 при условии, что
при условии, что 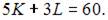
Так как при решении задачи на условный экстремум вида
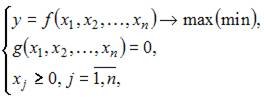
функция Лагранжа имеет вид
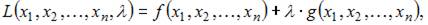
то в нашем случае можно использовать следующую функцию Лагранжа:
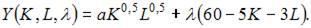
5. В процессе производства используются два вида ресурсов: капитал K и труд L. Функция выпуска имеет вид 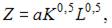 на аренду фондов (капитала) и оплату труда выделено 40 у.е., стоимость аренды единицы фондов равна 5 у.е., ставка заработной платы 4 у.е.
на аренду фондов (капитала) и оплату труда выделено 40 у.е., стоимость аренды единицы фондов равна 5 у.е., ставка заработной платы 4 у.е.
При решении задачи на максимизацию объема выпуска функция Лагранжа имеет вид …
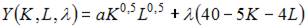 - правильно
- правильно
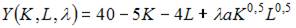
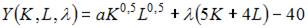
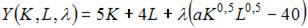
Решение:
Задача максимизации объема производства представляет собой задачу на условный экстремум, в которой 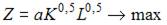 при условии, что
при условии, что 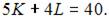
Так как при решении задачи на условный экстремум вида
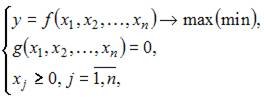
функция Лагранжа имеет вид
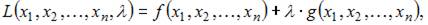
то в нашем случае можно использовать следующую функцию Лагранжа:
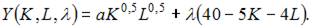
Кейс 2 подзадача 2
1. В процессе производства используются два вида ресурсов: капитал K и труд L. Функция выпуска имеет вид 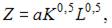 на аренду фондов (капитала) и оплату труда выделено 90 у.е., стоимость аренды единицы фондов равна 3 у.е., ставка заработной платы 5 у.е.
на аренду фондов (капитала) и оплату труда выделено 90 у.е., стоимость аренды единицы фондов равна 3 у.е., ставка заработной платы 5 у.е.
Наибольший объем выпуска достигается при значении K, равном …
Решение:
Вычислим частные производные первого порядка функции Лагранжа:
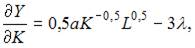
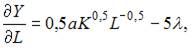
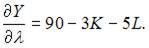
Приравняв их к нулю, получим систему уравнений:
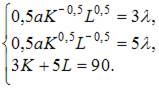
Найдем решение этой системы 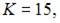
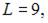
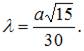 Тогда, согласно экономическому смыслу этой задачи, наибольший объем выпуска достигается при значении K = 15.
Тогда, согласно экономическому смыслу этой задачи, наибольший объем выпуска достигается при значении K = 15.
2. В процессе производства используются два вида ресурсов: капитал K и труд L. Функция выпуска имеет вид 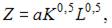 на аренду фондов (капитала) и оплату труда выделено 60 у.е., стоимость аренды единицы фондов равна 3 у.е., ставка заработной платы 4 у.е.
на аренду фондов (капитала) и оплату труда выделено 60 у.е., стоимость аренды единицы фондов равна 3 у.е., ставка заработной платы 4 у.е.
Наибольший объем выпуска достигается при значении K, равном …
Решение:
Вычислим частные производные первого порядка функции Лагранжа:
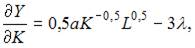
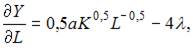
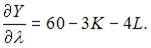
Приравняв их к нулю, получим систему уравнений:
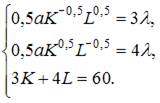
Найдем решение этой системы 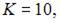
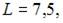
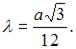 Тогда, согласно экономическому смыслу этой задачи, наибольший объем выпуска достигается при значении K = 10.
Тогда, согласно экономическому смыслу этой задачи, наибольший объем выпуска достигается при значении K = 10.
3. В процессе производства используются два вида ресурсов: капитал K и труд L. Функция выпуска имеет вид 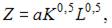 на аренду фондов (капитала) и оплату труда выделено 80 у.е., стоимость аренды единицы фондов равна 4 у.е., ставка заработной платы 5 у.е.
на аренду фондов (капитала) и оплату труда выделено 80 у.е., стоимость аренды единицы фондов равна 4 у.е., ставка заработной платы 5 у.е.
Наибольший объем выпуска достигается при значении L, равном …
Решение:
Вычислим частные производные первого порядка функции Лагранжа:
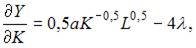
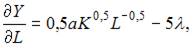
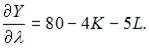
Приравняв их к нулю, получим систему уравнений:
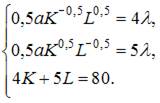
Найдем решение этой системы 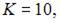
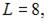
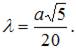 Тогда, согласно экономическому смыслу этой задачи, наибольший объем выпуска достигается при значении L = 8.
Тогда, согласно экономическому смыслу этой задачи, наибольший объем выпуска достигается при значении L = 8.
4. В процессе производства используются два вида ресурсов: капитал K и труд L. Функция выпуска имеет вид 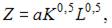 на аренду фондов (капитала) и оплату труда выделено 60 у.е., стоимость аренды единицы фондов равна 5 у.е., ставка заработной платы 3 у.е.
на аренду фондов (капитала) и оплату труда выделено 60 у.е., стоимость аренды единицы фондов равна 5 у.е., ставка заработной платы 3 у.е.
Наибольший объем выпуска достигается при значении K, равном …
Решение:
Вычислим частные производные первого порядка функции Лагранжа:
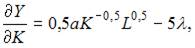
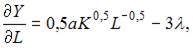
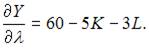
Приравняв их к нулю, получим систему уравнений:
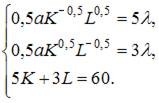
Найдем решение этой системы 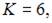
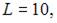
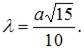 Тогда, согласно экономическому смыслу этой задачи, наибольший объем выпуска достигается при значении K = 6.
Тогда, согласно экономическому смыслу этой задачи, наибольший объем выпуска достигается при значении K = 6.
