Отработка навыка решения линейного уравнения с параметром
Решить уравнение
а) ( 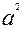 -9)х=а+3
-9)х=а+3
б)(а-1)(а-5)х=а-5
в)(а-3)(а+5)х= 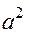 -25
-25
г) 6(ах-1)+а=3(а-х)+7
д) при каких значениях а уравнение 2(3х-2а)=2+ах не имеет решения ?
е) при каких значениях а уравнение 6(ах-1)-а=2(а+х)-7 имеет бесконечное множество решений ?
ж) при каких значениях а уравнение 2(а-2х)=ах+3 не имеет решения?
З) при каких значениях а уравнение 2(а+х)=3(1-х) имеет положительное решение?
и) при каких значениях а уравнение а(х-3)=2х+1 имеет решение , удовлетворяющее условию х<3?
Пример 1. Для всех значений параметра а решите уравнение 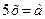 .
.
Ответ: 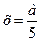 если а – любое число.
если а – любое число.
Пример 2. Для всех значений параметра а решите уравнение 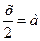 .
.
Ответ: 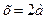 , если а – любое число.
, если а – любое число.
Пример 3. Для всех значений параметра а решите уравнение ах = 1.
Решение: При а = 0 данное уравнение решений не имеет, и в ответе это обстоятельство должно быть отражено.
Ответ: при а = 0 решений нет; при а ≠ 0 решение 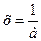 .
.
Пример 4. Для всех значений параметра а решите уравнение 0х = а.
Ответ: при а ≠ 0 корней нет;при а=0 х – любое число.
 Пример 5. Исследовать и решить уравнение с параметром
Пример 5. Исследовать и решить уравнение с параметром 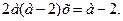
Решение: Найдём контрольные значения параметра, т.е. Такие значения при которых коэффициент при х обращается в 0. Такими значениями являются а = 0 и а = 2.
а)При а =0 уравнение принимает вид 0х = -2. Это уравнение корней не имеет.
б) При а = 2 уравнение принимает вид 0х = 0. Корнем этого уравнения является любое действительное число.
в) При а ≠ 0 и а ≠ 2 из исходного уравнения получаем 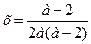 , откуда
, откуда 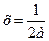 .
.
Ответ: 1) при а =0 корней нет.
2) при а = 2 х – любое действительное число.
3) при 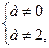 то
то 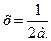
Пример 6. Исследовать и решить уравнение с параметром.
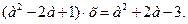
Найдём контрольные значения параметра а: 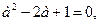
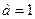 .
.
а) при а=1 уравнение принимает вид 0х = 0. Корнем этого уравнения является любое действительное число.
б) при а ≠ 1 уравнение примет вид 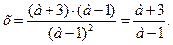
Ответ: 1) при а=1 х – любое действительное число.
2) при а ≠ 1 , то 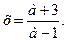
Пример 7. Исследовать и решить уравнение с параметром.
а2 (х – 5) = 25 (х – а)
Выполнив ряд преобразований, приведём уравнение к виду, наиболее удобному для исследования: а2х – 5а2 = 25х – 25а ;
(а2 – 25)х = 5а2 – 25а.
(а-5)(а+5)х = 5а(а-5).
а) при 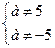
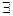 ед. х
ед. х 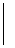
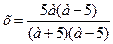 ;
; 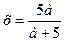 .
.
б) Если а = 5, то 0х = 0, следовательно, любое х есть решение.
в) Если а = - 5, то 0х = 250, следовательно, решений нет.
Графическая иллюстрация исследования по параметру а:
 -5 5
-5 5
а
3) 1) 2)
Ответ: 1) при 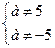
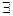 ед. х
ед. х 
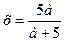 .
.
2) при а = 5, любое х есть решение.
