Скалярные и векторные поля

Московский Государственный Технический Университет

Имени Н.Э. Баумана

Добрица Б.Т., Дубограй И.В., Скуднева О.В.

Теория поля

Методические указания к выполнению домашнего задания.

Москва

Издательство МГТУ им. Н.Э. Баумана

Рецензент Покровский Л.Д.

Добрица Б.Т., Дубограй И.В., Скуднева О.В.

Теория поля: Методические указания к практическим занятиям.-

М.: Изд-во МГТУ им. Н.Э. Баумана, 2007, -43с.

Борис Тимофеевич Добрица

Ирина Валерьевна Дубограй

Оксана Валентиновна Скуднева

Теория поля

Тираж 1500 экз.
Введение.

Данные методические указания предназначены для работы студентов второго курса всех специальностей при изучении темы «Теория поля».

В работе кратко изложены все необходимые сведения из теории, подробно разобраны решения типовых задач.

Разделы «указаний» полностью соответствуют программе обучения студентов, утверждённой методической комиссией МГТУ им. Н.Э.Баумана.

Указания можно использовать как для самостоятельной работы, так и для проведения занятий в аудитории.

Скалярные и векторные поля.

Скалярное поле.Пусть G – область в трёхмерном пространстве или на плоскости. Тогда, если любой точке 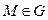поставлено в соответствие по некоторому правилу число 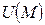, то говорят, что в области G задано скалярное поле.

Примеры физических скалярных полей: поле плотностей масс какого-либо тела; поле плотностей электрических зарядов на какой-либо поверхности или в сплошной среде; поле температур тела, поверхности или стержня и т. д. Физические скалярные поля не зависят от выбора системы координат, величина 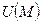является лишь функцией точки М. Если, кроме того, функция 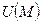зависит от времени t, поле называется нестационарным. Такие поля в данной работе не рассматриваются.

Если в пространстве задана декартова система координат Oxyz, то скалярное поле описывается функцией трёх переменных:

, .

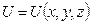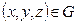Векторное поле. Говорят, что в области G задано векторное поле, если каждой точке 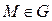поставлен в соответствие по некоторому правилу (закону) вектор 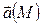. Задание векторного поля адекватно заданию вектор -функции 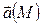с областью определения G. Если G - область трёхмерного пространства 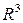с введённой в ней декартовой системой координат Oxyz с ортами 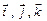, направленными по осям, то задание векторного поля равносильно заданию трёх скалярных функций-координат, каждая из которых зависит от трёх переменных: .

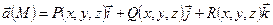Если G - область на плоскости 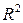, то в декартовых координатах скалярное поле задаётся функцией двух переменных 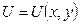, а векторное поле – двумя функциями двух переменных 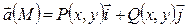. В этом случае поле называется плоским.

Физические примеры векторных полей: электрическое поле системы электрических зарядов, характеризующееся в каждой точке вектором напряжённости электрического поля 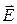; магнитное поле, создаваемое электрическим током и характеризующееся в каждой точке 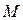вектором магнитной индукции 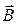; поле сил тяготения, создаваемое системой масс и характеризующееся в каждой точке 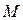вектором силы тяготения 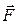, действующей в этой точке на единичную массу; поле скоростей потока движущейся жидкости, описываемое в каждой точке вектором скорости .

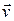Поля 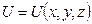и 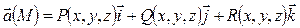называются дифференцируемыми n раз, если функции , , ,

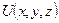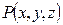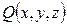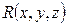
дифференцируемы n раз. В дальнейшем будем считать, что рассматриваемое поле дифференцируемо нужное нам число раз.