Построение графика функции двух переменных с помощью встроенной функции CreateMesh

Для построения графика функции двух переменных (поверхностей) в MathCAD 2001 предусмотрена встроенная функция CreateMesh.Функция CreateMeshпостроение графиков поверхностей,которые могут быть построены с помощью задания матрицы аппликат. Применение этой функции избавляет пользователя от задания матрицы аппликат в явном виде, так как эта матрица “самостоятельно” создается программой функции CreateMesh.

Пусть задана функция двух переменных

f(x, y) = 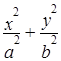. (7)

Функция CreateMeshв общем виде имеет восемь аргументов. Но для построения графика поверхности достаточно пяти аргументов. В этом случае функция CreateMeshимеет вид

CreateMesh (f, x0, x1, y0, y1),

где f – функция двух переменных, например (7); x0 – минимальное значение аргумента x; x1 – максимальное значение аргумента x; y0 - минимальное значение аргумента y; y1 - максимальное значение аргумента y.

Для построения графика поверхности с помощью функции CreateMeshследует:

1) задать функцию двух переменных;

2) задать границы изменения обоих аргументов;

3) задать функцию S:= CreateMesh (. . . . . . );

9) набрать и выполнить команду: Insert – Graph – Surface Plot;

10) в структурную метку шаблона графика, расположенную около начала координат, ввести имя функции “S”.

Подчеркнем, что здесь обозначение “S” – произвольно и при построении графика оно может быть выбрано любым.

Фрагмент программы MathCAD для построения графика поверхности с помощью функции CreateMeshприведен на рис. 17.

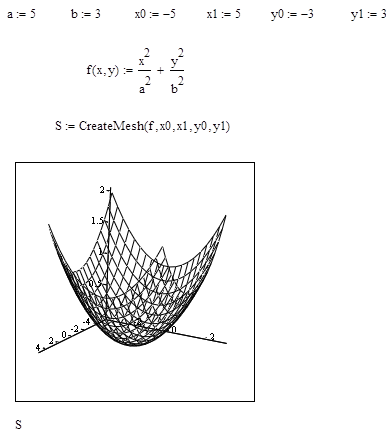
Рис. 17.

Отметим, что если поверхность не может быть построена с помощью задания матрицы аппликат, то она не будет построена с помощью функции CreateMesh.В частности это относится к уже упоминавшимся поверхностям эллипсоида, двуполостного и однополостного гиперболоидов и т. д.

Пусть на плоскости XOY задана некоторая кривая y = f (x) (a £ x £ b), где f (x) - непрерывна.

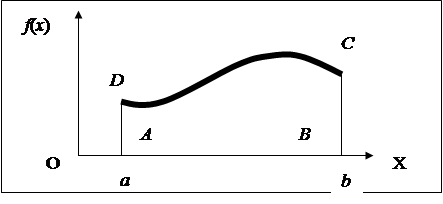
Рис. 18.

Если вращать такую линию вокруг оси OX, то получим некоторую фигуру, поверхность которой называют поверхностью вращения. В ранних версиях MathCAD (например, MathCAD 7) для построения графика поверхности вращения необходимо было перейти к заданию функции в параметрической форме. В MathCAD 2001 для построения графика поверхности вращения может быть использована функция CreateSpaceв виде

CreateSpace (F, G, H, a, b, q1, q2, N).

Здесь F, G, H – функции, определяемые уравнениями

F (x,q) = x, G (x,q) = f (x) cos (q), H (x,q) = f (x) sin (q),

где q - угол (см. рис. 20), a – минимальное значение x, b – максимальное значение x, q1 - минимальное значение угла q, q2 - максимальное значение угла q, N – количество линий, которые будут изображены на графике поверхности вращения.

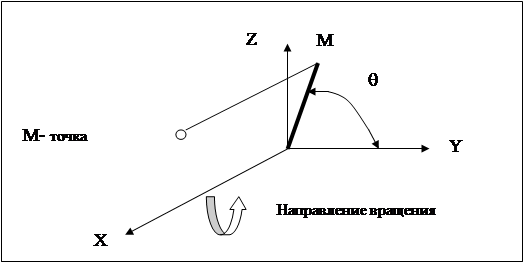
Рис. 19.

Для построения графика поверхности вращения следует:

1) задать функцию f (x), границы изменения аргумента x и границы изменения угла q;

2) задать функции F (x,q), G (x,q), H (x,q);

3) задать функцию S:= CreateMesh (. . . . . . );

4) набрать и выполнить команду: Insert – Graph – Surface Plot;

5) в структурную метку шаблона графика, расположенную около начала координат, ввести имя функции “S”.

Фрагмент программы MathCAD для построения графиков поверхностей вращения с помощью функции CreateMeshприведен на рис. 20, 21.

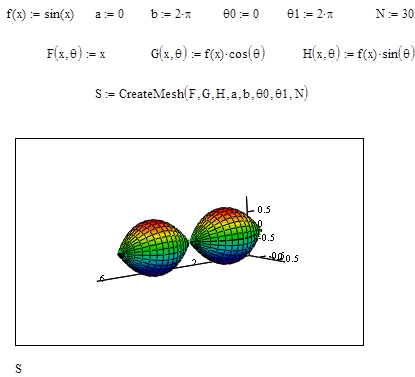
Рис. 20.

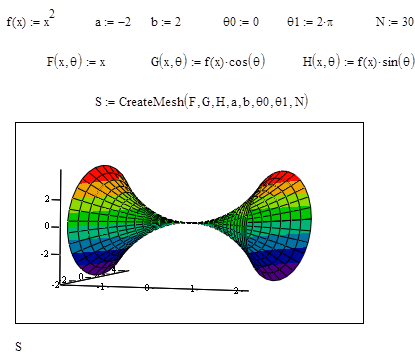
Рис. 21.

Границы a, b, q1, q2 изменения аргументов x,q можно не задавать отдельно в пункте 1 построения графика, а непосредственно указывать их значения в списке аргументов функции CreateMeshв пункте 3 построения графика.

Построение точечного графика поверхности и точечного графика линии в пространстве.

3.6.1. Построение точечного графика поверхности.

Во всех вариантах построения графика поверхности, рассмотренных в разделах 3.1–3.5, на построенной поверхности присутствует сетка линий. Напомним, что в этом случае шаблон графика выводится на экран в результате выполнения команды: Insert – Graph – Surface Plot.

Существует вариант построения графика поверхности, когда на построенной поверхности изображаются точки. В этом случае шаблон графика выводится на экран в результате выполнения команды: Insert – Graph – 3D Scatter Plot. Во всем остальном построение точечного графика поверхности полностью совпадает с построением обычного графика поверхности. Это означает, что точечный график поверхности может быть построен всеми методами, рассмотренными в разделах 3.1–3.5:

- с заданием матрицы аппликат;

- без задания матрицы аппликат;

- по параметрическому заданию поверхности;

- по векторному параметрическому заданию поверхности;

- с помощью функции CreateMesh. В том числе, с помощью функции CreateMesh может быть построен точечный график поверхности вращения.

Примеры построения точечного графика поверхности приведены на рис. 22,23.

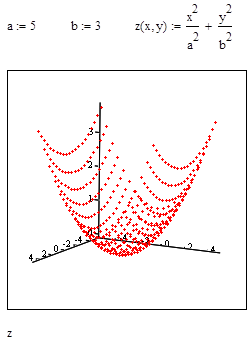
Рис.22. Поверхность эллиптического параболоида (без задания матрицы аппликат)

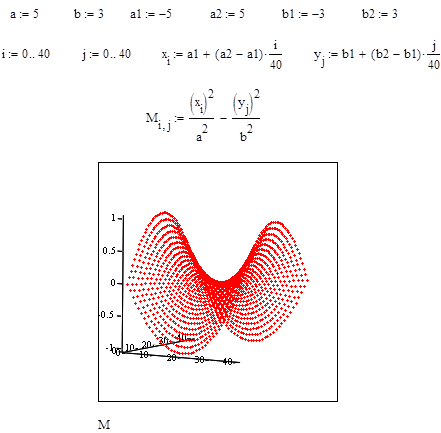
Рис.23. Поверхность гиперболического параболоида (без задания матрицы аппликат).

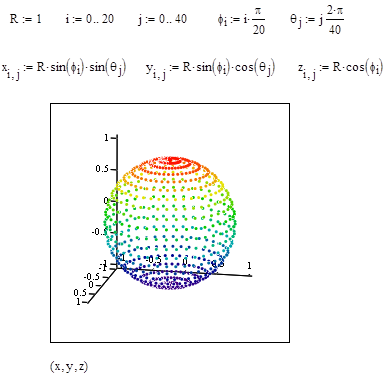
Рис. 24. Поверхность сферы (параметрическое задание).

3.6.2. Построение точечного графика линии в пространстве.

Явным способом задания линии в пространстве называют такой , когда две текущие координаты , например, y и z задаются в виде функций от третьей координаты x:

y = f (x), z = g (x). (8)

В общем случае пространственную линию рассматривают, как пересечение двух поверхностей, определяемых уравнениями

F (x, y, z) = 0, G (x, y, z) = 0. (9)

Уравнения (9) называют неявными уравнениями линии в пространстве.

Кроме этих способов задания существует параметрический способ задания пространственной линии (пространственной кривой). При параметрическом способе координаты x, y, z точки пространственной кривой задают как функции от некоторой другой переменной t, называемой параметром:

x = x (t); y = y (t); z = z (t). (10)

Запишем координаты (10) в виде вектора

H (t): = 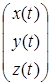. (11)

Для построения пространственной кривой в MathCAD 2001 предусмотрена функция CreateSpace. Она имеет вид CreateSpace (H, t1, t2, N), где H – функция, определяемая (11); t1 – минимальное значение параметра t; t2 – максимальное значение параметра t; N –число точек, наносимых на график построенной линии.

Для построения графика пространственной линиис помощью функции CreateSpace следует:

4) задать пространственную линию в векторной параметрической форме (задать функцию (11));

5) задать границы изменения параметра и число точек на графике линии;

6) задать функцию S:= CreateSpace (. . . . . . );

11) набрать и выполнить команду: Insert – Graph – 3D Scatter Plot;

12) в структурную метку шаблона графика, расположенную около начала координат, ввести имя функции “S”.

В качестве примера на рис. 25 приведено построение винтовой линии с помощью функции CreateSpace.

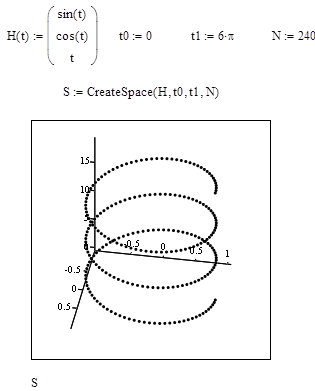
Рис. 25.

Предусмотрена также возможность построения точечного графика пространственной линии , когда координаты линии задаются в виде функций двух параметров, например x = x (h, q); y = y (h, q); z = z (h, q). В этом случае параметры h, q - индексированные переменные, зависящие только от одного индекса: h_i, q_i. Этот вариант построения графика линии аналогичен построению графика поверхности, заданной в параметрической форме. Отличие в том, что шаблон графика для линии выводится на экран с помощью команды: Insert – Graph – 3D Scatter Plot. Напомним также, при построении графика поверхности параметры h, q зависели от различных индексов: h_i, q_j.

Примеры построения графиков пространственных линий данным способом приведены на рис. 26, 27.

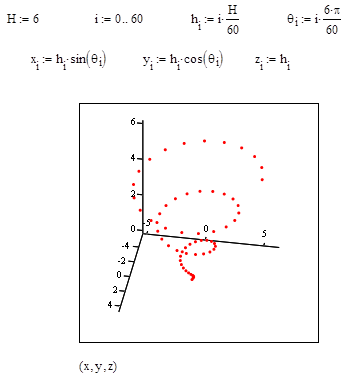
Рис. 26.Винтовая линия на поверхности конуса.

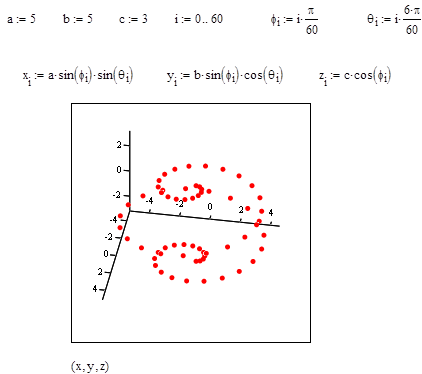
Рис. 27.Винтовая линия на поверхности эллипсоида.