Список использованных источников. подпись, дата инициалы, фамилия

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ

ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ

Преподаватель __________ ______________

подпись, дата инициалы, фамилия

Студент ДС 11-12 _________ Кудрявцев.Н.В

номер группы номер зачетной книжки подпись, дата инициалы, фамилия

Красноярск 2013

СОДЕРЖАНИЕ

Содержание …………………………………………………………………………….2

1. Цель и задачи лабораторной работы…………………………………………3

2. Теория.……………………………………………………………………..……..3

3. Физическая постановка задачи……………………………………………….4

4. Нахождение частот собственных колебаний балки...........................................4

5. Задача на нахождение четырех собственных значения......…………………6

6. Нахождение собственных значений и собственные вектора матрицы………7

Вывод…………………………………………………………………….……….........11

Список использованных источников…………………………………….…………..11

ЦЕЛЬ И ЗАДАЧИ ЛАБОРАТОРНОЙ РАБОТЫ

Цель: .

Задачи:

- научиться решать нелинейные алгебраические уравнения методами деления отрезка пополам и графическим;

- реализовать алгоритмы решения с помощью программы Excel;

- получить навыки отладки программы;

- оценить эффективность и область применения данных методов.

Теория.

А-квадратичная матрица.

Собственный вектор матрицы А-вектор, для которого справедливо уравнение:

Аȳ=λȳ, где λ-собственное значение матрицы.

Преобразуем Аȳ=λЕȳ, Аȳ-λЕȳ=0 , где Е-единичная матрица.

Или (А-λЕ)ȳ=0

СЛАУ называется однородной, если у нее правая часть равна нулю

Если det≠0, то у системы Ǝ! Тривиальное решение=0

Нетривиальное ȳ≠0, когда det(A-λE)=0

Матрица коэф(A-λE) называется характеристической матрицей заданной матрицы А.

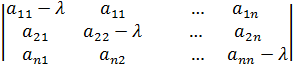
Корни уравнения – собственные значения λ _i(i=1,2…n)

Физическая постановка задачи

Найти частоты собственных колебаний балки.

Задача с 3-мя массами.

Силы инерции в виде усилий в упругих связях.

х_к=-mk 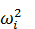y_ki ,где к=1,2,3.

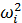-квадрат i-ой частоты свободных колебаний балки

y_ki-неизвестные перемещения к-ой точки массы при i-ой частоте колебания.

Однородная система канонических уравнений.

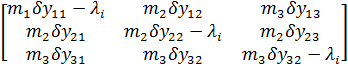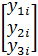х =0,

Где 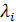= 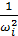, 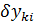- вариации перемещений (перемещение m_k от единицы силы, приложенной по направлению двух масс m_i)

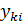- неизвестное перемещение точечных m_k при i-ой частоте свободных колебаний балки.

Решение задачи: λ³-а λ² +βλ-γ=0, где

а=а₁₁+ а₂₂ + а₃₃,

β=А₁₁+А₂₂+А₃₃-сумма алгебраических дополнений элементов а₁₁, а₂₂ , а_33.

γ=detA

Алгоритм решения.

1. Формируем матрицу А

2. Ищем коэффициенты уравнения λ³-а λ² +βλ-γ=0

3. Ищем графически корни

4. Находим частоты собственных колебаний

			вариации перемещений
m1	m2	m3	0,4101	-0,48	-0,584
	1,8	2,4	-0,1728	1,7111	0,48
			-0,28032	0,64	1,1953
Сформированная табл А		Поиск коэффициентов уравнения
2,0505	-0,864	-1,4016		α=		7,9992		A11=	7,508496
-0,864	3,07998	1,152		β=A11+A22+A33=	16,99533		A22=	3,917828
-1,4016	1,152	2,86872		γ=		9,99422		A33=	5,569003

	Найдем частоты уравнения
	ω=1/λ^(1/2	λ1=			ω1=
			λ2=			ω2=	0,707107
			λ3=			ω3=	0,447214

λ	f(λ)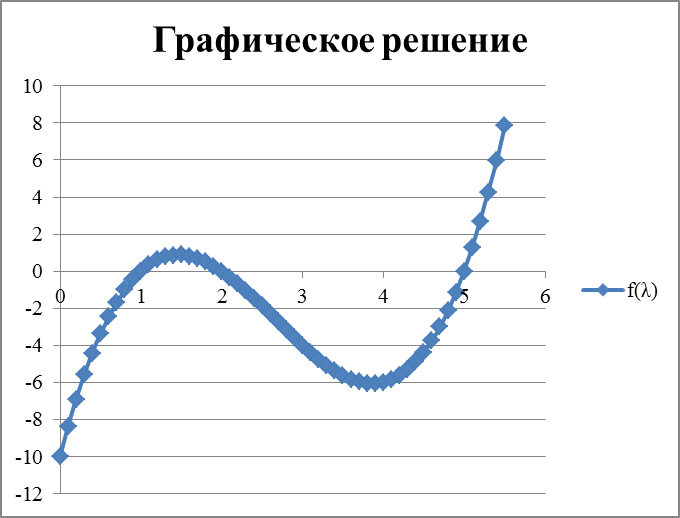
	-9,99422
0,1	-8,37368
0,2	-6,90712
0,3	-5,58855
0,4	-4,41196
0,5	-3,37136
0,6	-2,46074
0,7	-1,6741
0,8	-1,00545
0,9	-0,44878
	0,001907
1,1	0,352608
1,2	0,609324
1,3	0,778057
1,4	0,864806
1,5	0,875571
1,6	0,816351
1,7	0,693148
1,8	0,511961
1,9	0,278789
	-0,00037
2,1	-0,31951
2,2	-0,67263
2,3	-1,05374
2,4	-1,45683
2,5	-1,8759
…
4,8	-2,12622
4,9	-1,12891
	0,002415
5,1	1,273756
5,2	2,691113
5,3	4,260485
5,4	5,987874
5,5	7,879279

Задача на 4 собственные значения

λ⁴- а λ³+η λ² –βλ+γ=0

а=а₁₁+ а₂₂ + а₃₃ +а₄₄,

η=В₁₂+В₁₃+В₁₄+В₂₃+В₂₄+В₃₄ (сумма миноров 2-го порядка)

В_km=a_kk a_mm - a_km a_mk

β=А₁₁+А₂₂+А₃₃-сумма алгебраических дополнений элементов а₁₁, а₂₂ , а₃₃, а_44.

γ=detA

	A
	2,5		5,5
2,5
			40,5
5,5		40,5

a=
ŋ=	266,25
β=	90,25
γ=	6,0625

B12=	1,75	B13=		B14=	33,75
B23=		B24=		B34=	87,75

A11=				=
			40,5
		40,5
A22=			5,5	=
			40,5
	5,5	40,5

A33=		2,5	5,5	=
	2,5
	5,5
A44=		2,5		=	3,25
	2,5

λ1=	0,091		λ3=	2,343
λ2=	0,293		λ4=	97,272

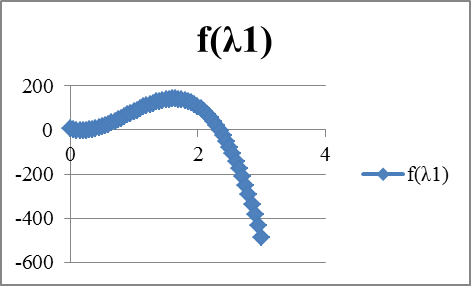
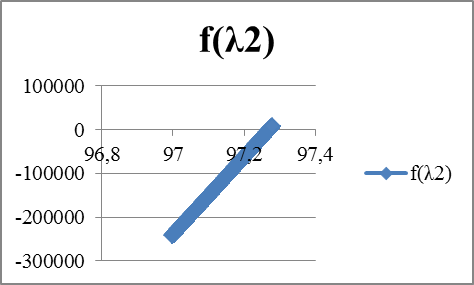
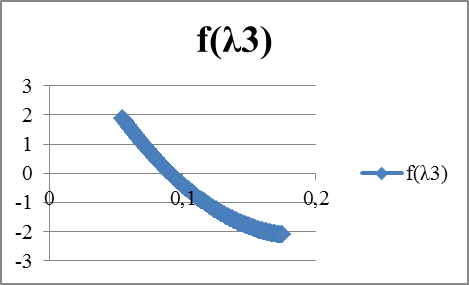
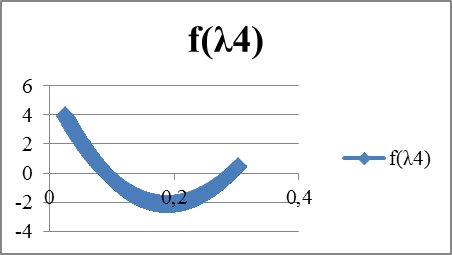
λ	f(λ)	λ	f(λ1)	λ	f(λ2)	λ	f(λ3)	λ	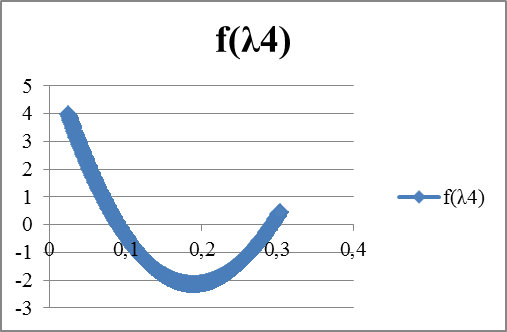f(λ4)
	83,0625		6,0625	97,262	-9276,58	0,055	1,887528	0,284	-0,37797
	106,5625	0,05	2,203131	97,263	-8382,46	0,056	1,825908	0,285	-0,34091
	-487,438	0,1	-0,3999	97,264	-7488,29	0,057	1,764788	0,286	-0,30349
	-2238,94	0,15	-1,82137	97,265	-6594,06	0,058	1,704165	0,287	-0,26571
	-5663,94	0,2	-2,1359	97,266	-5699,78	0,059	1,64404	0,288	-0,22757
	-11254,4	0,25	-1,41797	97,267	-4805,45	0,06	1,584413	0,289	-0,18906
	-19478,4	0,3	0,2581	97,268	-3911,05	0,061	1,525282	0,29	-0,1502
	… -1093842	0,35	2,818131	97,269	-3016,6	0,088	0,114253	0,291	-0,11098
	-241621	2,25	37,45703	97,27	-2122,1	0,089	0,068782	0,292	-0,0714
	665842,6	2,3	18,2341	97,271	-1227,54	0,09	0,023791	0,293	-0,03146
		2,35	-2,94887	97,272	-332,924	0,091	-0,02072	0,294	0,008838
		2,4	-26,1599	97,273	561,7477	0,092	-0,06476	0,295	0,049492
		2,45	-51,4669	97,274	1456,475	0,093	-0,10831	0,296	0,090503
		2,5	-78,9375	97,275	2351,258	0,094	-0,1514	0,297	0,13187
		2,55	-108,639	97,276	3246,097	0,095	-0,194	0,298	0,173592
		2,6	-140,64	97,277	4140,991	0,096	-0,23613	0,299	0,215669
		2,65	-175,006	97,278	5035,941	0,097	-0,27778	0,3	0,2581
		2,7	-211,806	97,279	5930,947	0,098	-0,31896	0,301	0,300885
		2,75	-251,105					0,302	0,344022
		2,8	-292,972					0,303	0,387512
		2,85	-337,472					0,304	0,431354
		2,9	-384,672
		2,95	-434,638
			-487,438

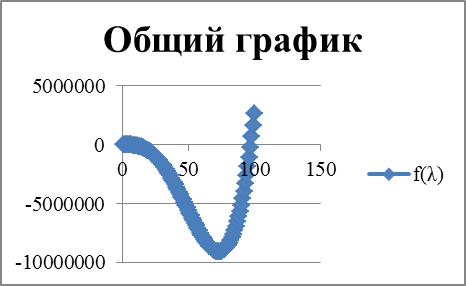Найти собственное значение и собственные векторы матрицы.

	-1
-1		-9
	-9
α
β	-51
γ	-259

A11	-61
A22	-5
A33

f(λ)=λ^3-αλ^2+βλ-λ=0

∆λ	0,1

0,9	-1
-1	0,9	-9
	-9	1,9
	-1,111111111	5,5555556
	-0,9
	-1,8	0,38
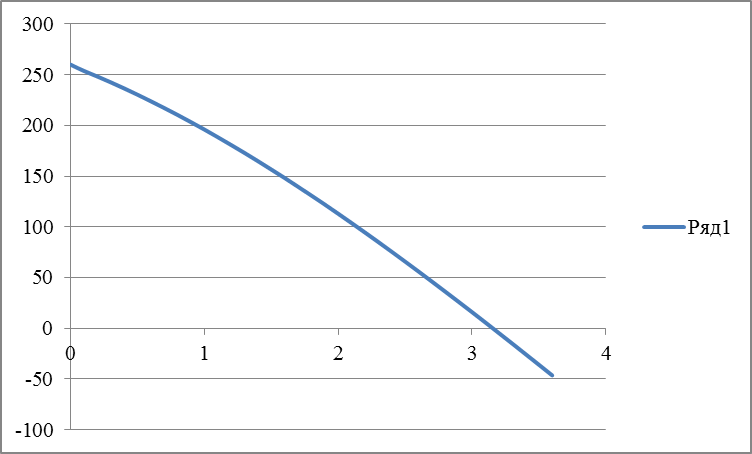	0,1	253,771
	0,2	248,288
	0,3	242,557
	0,4	236,584
	0,5	230,375
	0,6	223,936
	0,7	217,273
	0,8	210,392
	0,9	203,299
	1,1	188,501
	1,2	180,808
	1,3	172,927
	1,4	164,864
	1,5	156,625
	1,6	148,216
	1,7	139,643
	1,8	130,912
	1,9	122,029
				λ₁	3,1
	2,1	103,831
	2,2	94,528		ώ₁	56,096
	2,3	85,097
	2,4	75,544
	2,5	65,875
	2,6	56,096
	2,7	46,213
	2,8	36,232
	2,9	26,159
	3,1	5,761
	3,2	-4,552
	3,3	-14,933
	3,4	-25,376
	3,5	-35,875
	3,6	-46,424
	3,7
	3,8

ВЫВОД

Научились находить собственные значения и вектора матрицы.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров: учеб. пособие. М.: Высш. шк. – 1994. - 544 с.