Найти дивергенцию векторного поля
22. 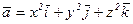 . 23.
. 23. 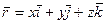 ..
..
24. 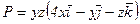 . 25.
. 25. 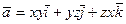 .
.
26. 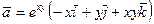 . 27.
. 27. 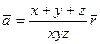 , где
, где 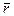 - радиус-вектор.
- радиус-вектор.
28. Найти дивергенцию поля градиента функции 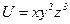 .
.
29. Найти 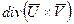 , где
, где 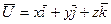 ,
, 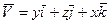 .
.
Циркуляция
Определение: Криволинейный интеграл по замкнутому контуру L от скалярного
произведения вектора 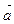 на вектор dr, касательный к контуру L, называется циркуляцией вектора а вдоль L
на вектор dr, касательный к контуру L, называется циркуляцией вектора а вдоль L
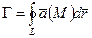 (1)
(1)
Другие формулы: 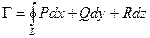 (2) – для решения задач
(2) – для решения задач
30. Найти циркуляцию вектора 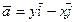 в положительном направлении вдоль замкнутой кривой, образованной осями координат и первой четвертью астроиды
в положительном направлении вдоль замкнутой кривой, образованной осями координат и первой четвертью астроиды 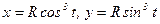 .
.
31. Найти циркуляцию вектора 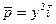 в положительном направлении по замкнутой, составленной из верхней половины эллипса
в положительном направлении по замкнутой, составленной из верхней половины эллипса 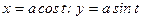 и отрезка оси
и отрезка оси 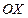 .
.
32. Вычислить циркуляцию векторного поля 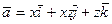 по контуру
по контуру 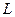 , образованному пересечением поверхности
, образованному пересечением поверхности 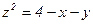 с плоскостями координат.
с плоскостями координат.
33. Вычислить циркуляцию векторного поля 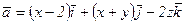 вдоль периметра треугольника с вершинами
вдоль периметра треугольника с вершинами 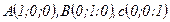 .
.
34. Вычислить циркуляцию векторного поля 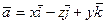 вдоль контура
вдоль контура 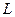 , являющегося линией пересечения поверхности
, являющегося линией пересечения поверхности 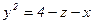
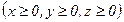 с координатными плоскостями.
с координатными плоскостями.
Ротор
Определение:
Ротором векторного поля 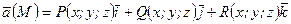 называется вектор вида
называется вектор вида
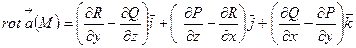
Ротор удобно находить с помощью символического вектора
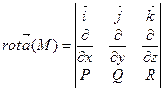
Найти ротор векторного поля
35. 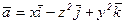 . 36.
. 36. 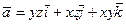 .
.
37. 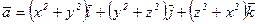 38.
38. 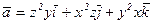 .
.
39. 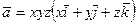 . 40.
. 40. 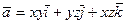 .
.
Основные вопросы по теме:
«Элементы теории поля»
1. Векторная функция скалярного аргумента
2. Скалярное поле. Линии и поверхности поля.
3. Производная по направлению Вывод формулы
4. Градиент и его свойства
5. Векторное поле. Виды векторных полей.
6. Векторные линии и их уравнения.
7. Поток вектора и его различные формы записи. Физический смысл потока.
8. Поток вектора через замкнутую поверхность.
9. Дивергенция и ее свойства.
10.Формула Остроградского в векторной форме. Физический смысл дивергенции
11.Циркуляция векторного поля и ее различные формы записи. Физический смысл циркуляции.
12. Потенциальные поля и их свойства.
13.Ротор и его свойства. Формула Стокса в векторной форме.
14. Векторные дифференциальные операции.
Тема № 3 Ряды
Литература:
1. Мальцева «Числовые ряды»
2. Письменный « Конспект лекций по высшей математике» кн 2
3. Пискунов «Дифференциальные и интегральные исчисления», т 2
Знакоположительные ряды
Определение.
1. Числовым рядом называется выражение вида:
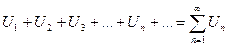 , где
, где 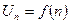 ;
;
2. Ряд задан, если известен закон по которому можно вычислить любой член ряда.
3. Конечная сумма n – первых членов называется частичной суммой ряда.
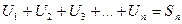
4. Ряд 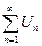 называется сходящимся, если существует конечный
называется сходящимся, если существует конечный 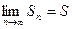 ;
;
6. Необходимый признак сходимости ряда
если ряд 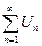 сходится, то
сходится, то 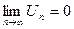 ; обратное утверждение неверно.
; обратное утверждение неверно.
7. Если 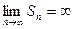 или не существует, то ряд называется расходящимся
или не существует, то ряд называется расходящимся
8. Ряд все члены которого либо положительные, либо отрицательные называется знакопостоянным.
9. Признаки сходимости и расходимости рядов с положительными членами
Дано: 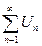 ,
, 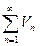 - знакоположительные ряды, где
- знакоположительные ряды, где 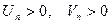 при всех
при всех 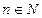
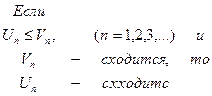 | Если все члены первого ряда не превосходят соответствующих членов второго ряда, то если сходится второй ряд, то сходится и первый | |
 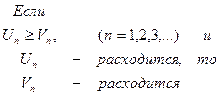 | Если все члены первого ряда не меньше соответствующих членов второго ряда, то если расходится второй ряд, то расходится и первый | |
3  | 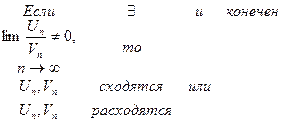 | Если 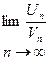 существует, конечен и отличен от нуля., то оба ряда либо одновременно сходятся, либо одновременно расходятся существует, конечен и отличен от нуля., то оба ряда либо одновременно сходятся, либо одновременно расходятся |
Эталонные ряды
| Название | Формула | Поведение | |
| Ряд геометрической прогрессии | 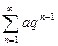 | 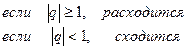 | |
| Гармонический ряд | 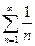 | 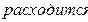 | |
| Обобщенный гармонический ряд | 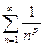 | 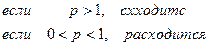 |
