Анализ спектра реакции в нелинейном элементе

Рассмотрим анализ на примере спектра тока при подаче гармонического напряжения. Если элемент линейный, то мы получаем гармонический ток (одна составляющая). Если элемент нелинейный, то получим много составляющих.

Для определения спектра, необходимо найти амплитуды спектральных составляющих и начальные фазы. Частоты всех составляющих будут кратны основной частоте или частоте воздействия. Самый простой способ – применить степенную аппроксимацию.

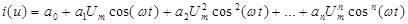
при 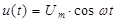(возьмем для упрощения U₀=0).

Затем необходимо воспользоваться формулами разложения:

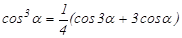
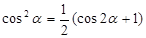
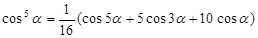
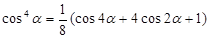
Число составляющих гармоник равно выбранной степени полинома, при этом четные степени полинома дают четные гармоники, нечетные – нечетные. Для 5 степени

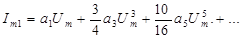
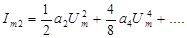
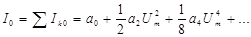
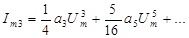
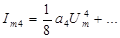
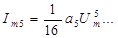
Начальные фазы всех составляющих нулевые.

Таким образом, можно приблизительно определить спектр. Можно определить спектры при других аппроксимациях, но это более сложно математически.

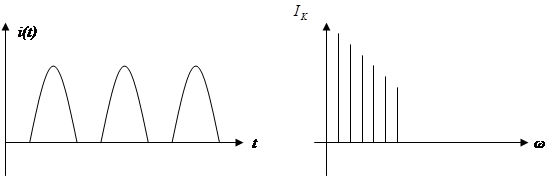
Временное представление Спектральное

Также применяют метод нескольких ординат.

В частности рассмотрим метод трех ординат.

Здесь берут 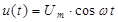и три значения переменной времени

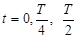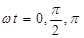( ), где Т- период (2π/ω). Затем определяют по характеристике три значения тока (три ординаты) i_max , i₀ и i_min. Далее ток рассматривают в виде трех составляющих

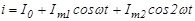и определяют токи по этому выражению.

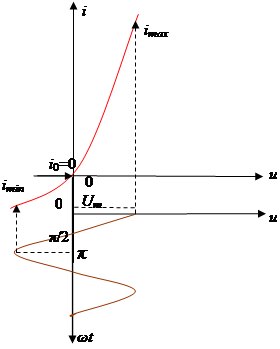
В итоге составляют систему уравнений с учетом значений косинуса 1,0,-1:

,

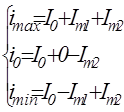Из которой находят амплитуды гармоник.

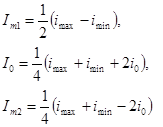
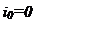Аналогично можно использовать большее количество точек (метод пяти, семи и т.д. ординат).

Метод пяти ординат.

t₁ = 0 (0) ,

t₂ = T/6 (π/3) ,

t₃ = T/4 (π/2) ,

t₄ = T/3 (2π/3) ,

t₅ = T/2. (π).

Cos(π/3)=1/2

Cos(2π/3)=-1/2

Cos(4π/3)=-1/2

Cos(8π/3)=-1/2

Ток в нелинейном элементе описывается уравнением вида:

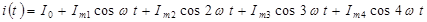, где .

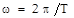Учитывая тот факт, что при t = 0, T/6, T/4, T/3, T/2 ток приобретает значения i_max, i₁, i₀, i₂, i_min соответственно, получим следующую систему из 5 алгебраических уравнений:

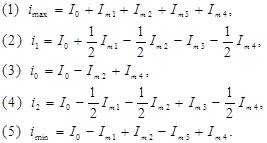
Решая данную систему уравнений относительно неизвестных спектральных составляющих можно найти амплитуды гармоник.

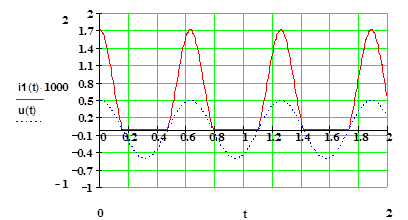
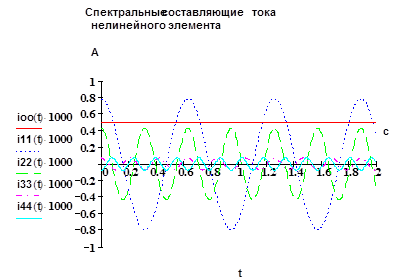
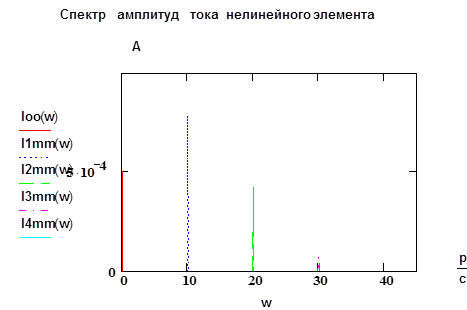
Пример расчета спектра импульсов тока и построения графиков (Mathcad 2001) по методу пяти ординат показан ниже. Здесь изображены сначала кривые тока нелинейного элемента (диода), далее гармонические составляющие тока во временном виде и потом амплитудный спектр в линейчатом виде. При этом показаны четыре гармонические составляющие и постоянная составляющая. Расчеты велись с использованием метода 5 ординат.

i(t)=I₀+I_1mcos(2 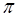f∙t)+I_2mcos(2 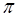2f∙t)+I_3mcos(2 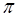3f∙t)+I_4mcos(2 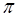4f∙t)

I₀=(i_max+i_min+2(i₁+i₂))/6 , I_1m=(i_max─i_min+i₁─i₂)/3,

I_2m=( i_max+i_min-─2i₀)/4, I_3m=( i_max─i_min─2(i₁─ i₂))/6,

I_4m=( i_max+i_min─4(i₁+i₂)─6i₀)/12

Вид тока НЭ (диода) при гармоническом напряжении при 0 смещении (U₀=0).

.

Преобразование сигналов в нелинейных цепях