Закон великих чисел, центральна гранична теорема

Нерівності Чебишова.

Перша форма: якщо випадкова величина Х невід’ємна і 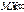, то

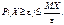
Друга форма: якщо для випадкової величини існують моменти першого та другого порядку, то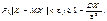

Нехай задано послідовність випадкових величин:

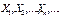
Послідовність (1) задовольняє закон великих чисел, якщо

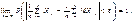
Окремі форми закону великих чисел різняться обмеженнями, які накладаються на випадкові величини, що входять у послідовність (1).

Теорема Хінчина. Якщо випадкові величини у послідовності незалежні, однаково розподілені і мають скінченне математичне сподівання 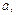то

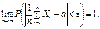
Теорема Чебишова. Якщо випадкові величини у послідовності (1) незалежні, мають скінченні математичні сподівання і рівномірно обмежені дисперсії 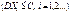, то до послідовності (1) можна застосувати закон великих чисел.

Теорема Маркова. Нехай випадкові величини в послідовності (1) мають скінченні і як завгодно залежні математичні сподівання. Тоді, якщо 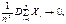при 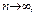то для послідовності (1) можна застосувати закон великих чисел.

Теорема Бернуллі. Нехай проводиться n незалежних повторних випробувань, у кожному з яких імовірність настання події А дорівнює р. Тоді

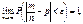
де 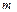— частота події А у даних випробуваннях.

Центральна гранична теорема.

Для послідовності випадкових величин 1) розглянемо:

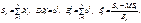
Теорема 1. Якщо випадкові величини в послідовності (1) незалежні, однаково розподілені і для них існують моменти другого порядку, то

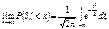(2)

тобто граничним розподілом для 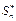є нормальний закон розподілу з нульовим математичним сподіванням і одиничною дисперсією.

Теорема Ляпунова. Якщо для незалежних випадкових величин, які утворюють послідовність (1), існують моменти третього порядку і виконується умова

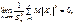то для 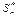виконується співвідношен-
ня (2).

Наслідком розглянутих теорем є інтегральна теорема Лапласа.

У схемі незалежних повторних випробувань

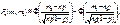
де 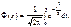Це випливає з того, що частоту події можна подати як суму n випадкових величин — частот настання події в окремих випробуваннях. При достатньо великих значеннях n закон розподілу цієї суми близький до нормального.

Аналогічними міркуваннями для цієї схеми легко дістати формулу:

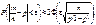де m — частота події А у n випробуваннях.

34)Нерівності Чебишова та її значення. Перша форма: якщо випадкова величина Х невід’ємна і 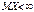, то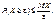

Зауваження : існує друга форм, якщо для випадкової величини існують моменти першого та другого порядку, то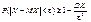

Нехай задано послідовність випадкових величин:

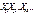(1)

Послідовність (1) задовольняє закон великих чисел, якщо

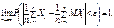
Окремі форми закону великих чисел різняться обмеженнями, які накладаються на випадкові величини, що входять у послідовність(1).

Теорема Чебишова

Нехай 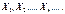послідовність незалежних випадкових величин ,які задовольняють умовам:

1.M(X_і)>= a_і

2.D(X_і )<= с Для всіх і=1,2,3…..n

Якщо випадкові величини у послідовності 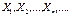незалежні, мають скінченні математичні сподівання і рівномірно обмежені дисперсії 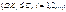, то до послідовності (1) можна застосувати закон великих чисел. Це означає що середне арифметичне достатньо великої кількості незалежних випадкових величин дуже мало відрізняється від середнього арифметичного їхніх математичних сподівань ,взятого за абсолютним значенням .

Ця теорема є законом великих чисел ,так само як і центральна гранична теорема

Теорема Бернулі

Нехай проводиться n незалежних повторних випробувань, у кожному з яких імовірність настання події А дорівнює р.Якщо ймовірність появи випадкової події А в кожному з незалежних випробувань n є величиною сталою і дорівнює P,то при необмеженому збільшенні числа експериментів n→∞

Імовірність відхилення відносної частоти появи випадкової події W(A) від імовірності p ,взятої за абсолютною величиною на ε(ε>0) прямуватиме до одиниці зі зростанням n ,що можна записати так:

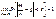
де 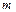— частота події А у даних випробуваннях. Таким чином при необмеженому збільшенні числа незалежних випробувань за схемою Бернулі відносна частота дуже мало відрізняється від ймовірності .

Наведена теорема є законом великих чисел ,так само як і центральна гранична теорема

37) Центральна гранична теорема. Для послідовності випадкових величин 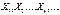розглянемо:

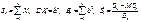
Теорема. Якщо випадкові величини в послідовності незалежні, однаково розподілені і для них існують моменти другого порядку, то

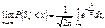
тобто граничним розподілом для 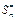є нормальний закон розподілу з нульовим математичним сподіванням і одиничною дисперсією.

Теорема Ляпунова. Якщо для незалежних випадкових величин, які утворюють послідовність 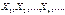, існують моменти третього порядку і виконується умова

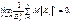то для 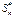виконується співвідношен-
ня (2).

Наслідком розглянутих теорем є інтегральна теорема Лапласа.

У схемі незалежних повторних випробувань

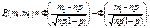
де 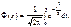Це випливає з того, що частоту події можна подати як суму n випадкових величин — частот настання події в окремих випробуваннях. При достатньо великих значеннях n закон розподілу цієї суми близький до нормального.

Аналогічними міркуваннями для цієї схеми легко дістати формулу:

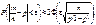де m — частота події А у n випробуваннях.

38) Випадковим процесом 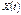називається процес, значення якого за будь-якого значення аргументу t є випадковою величиною.

Реалізацією випадкового процесу називається детермінована функція 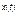, на яку перетворюється випадковий процес 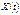внаслідок випробування, тобто його траєкторія.

Кілька реалізацій певного випадкового процесу зображено на рис. 4.1. Нехай переріз цього процесу при даному t є неперервною випадковою величиною. Тоді випадковий процес 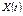при даному t визначається щільністю ймовірності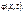

Очевидно, що щільність імовірності 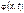не є вичерпним заданням випадкового процесу 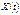, оскільки вона не виражає залежності між його перерізами в різні моменти часу.

Випадковий процес 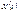являє собою сукупність усіх перерізів за всіх можливих значень t, тому для його задання необхідно розглядати багатовимірну випадкову величину 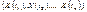утворену з усіх перерізів цього процесу.

Таких перерізів нескінченно багато, але для задання випадкового процесу вдається обмежитись порівняльно невеликою кількістю перерізів.

Випадковий процес має порядок п, якщо він повністю визначається щільністю спільного розподілу 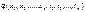п довільних перерізів процесу, тобто щільністю п-вимірної випадкової величини 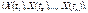де 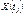— переріз випадкового процесу 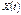у момент часу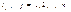

Випадковий процес може бути заданий числовими характеристиками.

Математичним сподіванням випадкового процесу 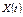називається детермінована функція 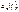яка за будь-якого значення змінної t дорівнює математичному сподіванню відповідного перерізу випадкового процесу 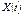, тобто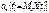

Дисперсією випадкового процесу 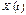називається детермінована функція 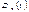, яка за будь-якого значення змінної t дорівнює дисперсії відповідного перерізу випадкового процесу 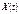, тобто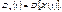

Середнім квадратичним відхиленням 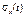випадкового процесу 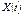називається арифметичне значення квадратного кореня з його дисперсії, тобто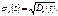

Математичне сподівання випадкового процесу характеризує середню траєкторію всіх можливих його реалізацій, а його дисперсія або середнє квадратичне відхилення

— розкид реалізацій відносно середньої траєкторії.

X = xi	x1	x2	x3	…	xk
ni	n1	n2	n3	…	nk
Wi	W1	W2	W3	…	Wk

39) Потоком подій називається послідовність подій, які відбуваються одна за одною у випадкові моменти часу. Наприклад, потік заявок, що надходить до підприємства побутового обслуговування, потік викликів до телефонної станції, потік відказів (збоїв) під час роботи на ПЕОМ тощо. Середня кількість подій, які відбуваються за одиницю часу, називається інтенсивністю потоку.

Потік називається найпростішим, якщо він має такі властивості:

стаціонарність— імовірність того, що за деякий проміжок часу t відбудеться та чи інша кількість подій, залежить лише від довжини проміжку і не залежить від початку його відліку, тобто інтенсивність потоку стала;

відсутність післядії — імовірність настання деякої кількості подій на довільному проміжку часу не залежить від того, яка кількість подій відбулась до початку цього проміжку;

ординарність— імовірність настання двох і більше подій за малий проміжок часу t істотно менша за ймовірність того, що відбудеться одна подія.

Якщо потік подій найпростіший, то ймовірність того, що за проміжок часу t подія А настане m раз, визначається формулою: 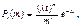де 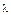— інтенсивність потоку. Ця формула відбиває всі властивостінайпростішого потоку, а отже, є його математичною моделлю.