Кинематика поступательного движения

ВВЕДЕНИЕ

Дидактический материал предназначен студентам всех специальностей заочного факультета ГУЦМиЗ, изучающих курс механики по программе для инженерно-технических специальностей.

Дидактический материал содержит краткое изложение теории по изучаемой теме, адаптированной к уровню обученности студентов-заочников, примеры решения типовых задач, вопросы и задания, аналогичные предлагаемым студентам на экзаменах, справочный материал.

Цель такого материала – помочь студенту-заочнику самостоятельно в сжатые сроки усвоить кинематическое описание поступательного и вращательного движений, используя метод аналогии; научиться решать численные и качественные задачи, разбираться в вопросах, связанных с размерностью физических величин.

Особое внимание уделяется решению качественных задач, как одному из приемов более глубокого и сознательного усвоения основ физики, необходимых при изучении специальных дисциплин. Они помогают понять смысл происходящих явлений природы, уяснить сущность физических законов и уточнить область их применения.

Дидактический материал может быть полезен студентам дневной формы обучения.

КИНЕМАТИКА

Часть физики, изучающую механическое движение, называют механикой. Под механическим движением понимают изменение с течением времени взаимного расположения тел или их частей.

Кинематика – первый раздел механики, она изучает законы движения тел, не интересуясь причинами, вызывающими это движение.

Материальная точка. Система отсчета. Траектория.

Путь. Вектор перемещения

Простейшая модель кинематики - материальная точка. Это тело, размерами которого в данной задаче можно пренебречь. Любое тело можно представить как совокупность материальных точек.

Чтобы математически описать движение тела, необходимо определиться с системой отсчета. Система отсчета (СО) состоит из тела отсчета и связанных с ним системы координат и часов. Если в условии задачи нет специальных указаний, считается, что система координат связана с поверхностью Земли. В качестве системы координат чаще всего используется декартова система.

Пусть требуется описать движение материальной точки в декартовой системе координат ХУZ (рис.1). В некоторый момент времени t₁ точка находится в положении А. Положение точки в пространстве можно характеризовать радиусом - вектором r₁, проведенным из начала координат в положение А, и координатами x₁, y₁, z₁. Здесь и далее векторные величины обозначены жирным курсивом. К моменту времени t₂ = t₁ + Δ t материальная точка переместится в положение В с радиус вектором r₂ и координатами x₂, y₂, z₂.

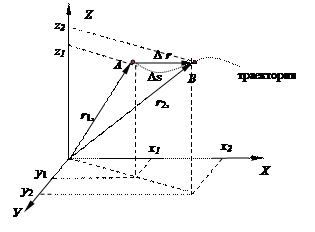Рис.1

Траекторией движения называется кривая в пространстве, по которой движется тело. По виду траектории различают прямолинейное, криволинейное движения и движение по окружности.

Длина пути (или путь) - длина участка АВ, измеренная по траектории движения, обозначается через Δs (или s). Путь в международной системе единиц (СИ) измеряется в метрах (м).

Вектор перемещения материальной точки Δr представляет собой разность векторов r₂ и r₁ , т.е.

Δr = r₂ - r_1.

Модуль этого вектора, называемый перемещением, является кратчайшим расстоянием между положениями А и В (начальным и конечным) движущейся точки. Очевидно, что Δs ≥ Δr, причем равенство выполняется при прямолинейном движении.

При движении материальной точки значение пройденного пути, радиуса-вектора и его координат меняется со временем. Кинематическими уравнениями движения (в дальнейшем уравнениями движения) называют их зависимости от времени, т.е. уравнения вида

s=s(t), r= r(t), x=х(t), y=у(t), z=z(t).

Если для движущегося тела известно такое уравнение, то в любой момент времени можно найти скорость его движения, ускорение и т.д., в чем далее убедимся.

Любое движение тела можно представить как совокупность поступательного и вращательного движений.

Кинематика поступательного движения