Что дает математическая модель сигнала

Понятие сигнала

В технических отраслях знаний термин сигнал –

1) техническое средство, для передачи обращения и использования информации.

2) физический процесс отображающих информационное сообщение (изменение какого либо параметра носителя информации)

3) смысловое содержание определённого физического состояния или процесса.

Сигнал – сведенья/ сообщения/ информация, о каких либо процессах / состояниях или физических величинах объектов материального мира, выраженных в форме удобной для передачи, обработки, хранения и использования этих сведений.

С математической точки зрения сигнал представляет собой функцию, то есть зависимость одной величины от другой.

Цель обработки сигналов

Целью обработки сигналов считают изучение определённых информационных сведений, которые отображены в виде целевой информации и преобразования этих сведений в форму удобную для дальнейшего использования.

Цель анализа сигналов

Под "анализом" сигналов (analysis) имеется в виду не только их чисто математические преобразования, но и получение на основе этих преобразований выводов о специфических особенностях соответствующих процессов и объектов.
Целями анализа сигналов обычно являются:
- Определение или оценка числовых параметров сигналов (энергия, средняя мощность, среднее квадратическое значение и пр.).
- Разложение сигналов на элементарные составляющие для сравнения свойств различных сигналов.
- Сравнение степени близости, "похожести", "родственности" различных сигналов, в том числе с определенными количественными оценками.

Регистрация сигналов

С понятием сигнала неразрывно связан термин регистрации сигналов, использование которого также широко и неоднозначно, как и самого термина сигнал. В наиболее общем смысле под этим термином можно понимать операцию выделения сигнала и его преобразования в форму, удобную для дальнейшего использования, обработки и восприятия. Так, при получении информации о физических свойствах каких-либо объектов, под регистрацией сигнала понимают процесс измерения физических свойств объекта и перенос результатов измерения на материальный носитель сигнала или непосредственное энергетическое преобразование каких-либо свойств объекта в информационные параметры материального носителя сигнала (как правило - электрического). Но так же широко термин регистрации сигналов используют и для процессов выделения уже сформированных сигналов, несущих определенную информацию, из суммы других сигналов (радиосвязь, телеметрия и пр.), и для процессов фиксирования сигналов на носителях долговременной памяти, и для многих других процессов, связанных с обработкой сигналов.

Внутренние и внешние источники шумов

Шумы, как правило, имеют стохастический (случайный) характер. К помехам относят искажения полезных сигналов при влиянии различных дестабилизирующих факторов (электрические наводки, вибрация, виды шумов и помех различают по источникам их возникновения, энергетическому спектру). По характеру воздействия на сигнал источники шумов и помех бывают внутренние и внешние.

Внутренние помехи присущи физической природе источников и детекторов сигналов, а также материальных носителей. Внешние источники помех бывают искусственного и естественного происхождения. К искусственным шумам относят индустриальные помехи и помехи от работающего оборудования.

Что дает математическая модель сигнала

Теория анализа и обработки физических данных базируется на математических моделях соответствующих физических полей и физических процессов на основе которых создаются математические модели сигналов они дают возможность обобщённо абстрагируясь от физической природы судить о свойствах сигналов, предсказывать изменения сигналов в различных условиях, кроме того появляется возможность игнорировать большое число второстепенных признаков. Знания математических моделей даёт возможность классифицировать сигналы по различным признакам (например, сигналы делят на детерминированные и стохастические).

Классификация сигналов

Классификация сигналов осуществляется на основании существенных признаков соответствующих математических моделей сигналов.Все сигналы разделяют на две крупных группы: детерминированные и случайные.

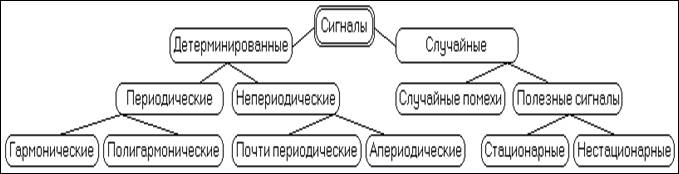
Гармонические сигналы

Гармонические сигналы (синусоидальные), описываются следующими формулами:

s(t) = A×sin (2f_оt+f) = A×sin (_оt+f), s(t) = A×cos(_оt+), (1.1.1)

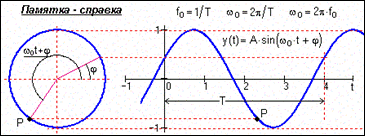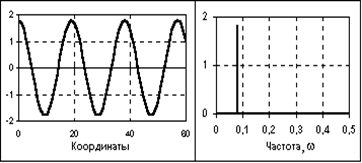Рис. 5. Гармонический сигнал и спектр его амплитуд

где А, f_o, _o, f - постоянные величины, которые могут исполнять роль информационных параметров сигнала: А - амплитуда сигнала, f_о - циклическая частота в герцах, _о= 2f_о - угловая частота в радианах,  и f- начальные фазовые углы в радианах. Период одного колебания T = 1/f_о = 2/_o. При j = f-p/2 синусные и косинусные функции описывают один и тот же сигнал. Частотный спектр сигнала представлен амплитудным и начальным фазовым значением частоты f_о (при t = 0).

Полигармонические сигналы

Полигармонические сигналы составляют наиболее широко распространенную группу периодических сигналов и описываются суммой гармонических колебаний:

s(t) = 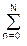A_n sin (2f_nt+_n) ≡ 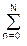A_n sin (2B_nf_pt+_n), B_n ∈ I, (1.1.2)

или непосредственно функцией s(t) = y(t ± kT_p), k = 1,2,3,..., где Т_р - период одного полного колебания сигнала y(t), заданного на одном периоде. Значение f_p =1/T_p называют фундаментальной частотой колебаний.

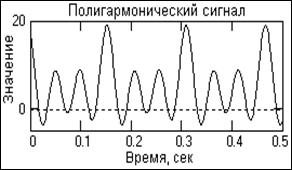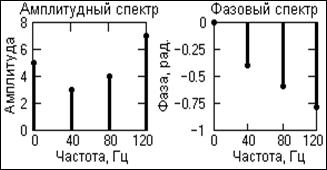Рис. 6. Модель сигнала Рис. 7. Спектр сигнала

Полигармонические сигналы представляют собой сумму определенной постоянной составляющей (f_о=0) и произвольного (в пределе - бесконечного) числа гармонических составляющих с произвольными значениями амплитуд A_n и фаз j_n, с частотами, кратными фундаментальной частоте f_p. Другими словами, на периоде фундаментальной частоты f_p, которая равна или кратно меньше минимальной частоты гармоник, укладывается кратное число периодов всех гармоник, что и создает периодичность повторения сигнала. Частотный спектр полигармонических сигналов дискретен, в связи с чем второе распространенное математическое представление сигналов - в виде спектров (рядов Фурье).