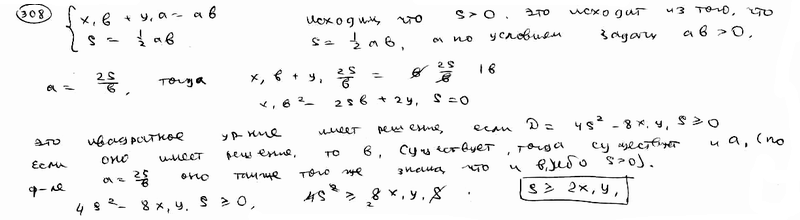| | | Определить, какие из точек M1(3; 1), M2(2; 3), M3(6; 3), M4(-3; -3), M5(3; -1), M6(-2; 1) лежат на прямой 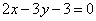 и какие на ней не лежат. и какие на ней не лежат. 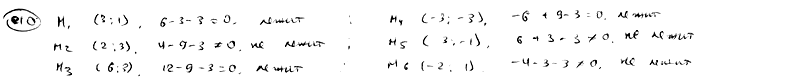 |
| | | Точки P1, P2, P3, P4, P5 расположены на прямой 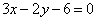 ; их абсциссы соответственно равны числам 4; 0; 2; -2; -6. Определить ординаты этих точек. ; их абсциссы соответственно равны числам 4; 0; 2; -2; -6. Определить ординаты этих точек. 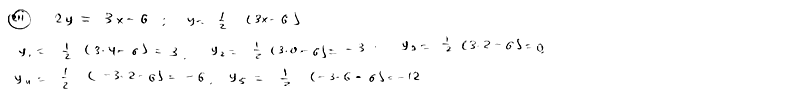 |
| | | Точки Q1, Q2, Q3, Q4, Q5 расположены на прямой 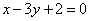 ; их ординаты соответственно равны числам 1; 0; 2; -1, 3. Определить абсциссы этих точек. ; их ординаты соответственно равны числам 1; 0; 2; -1, 3. Определить абсциссы этих точек. 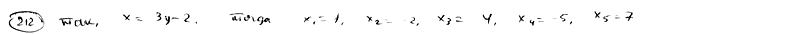 |
| | | Определить точки пересечения прямой 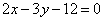 с координатными осями и построить эту прямую на чертеже. с координатными осями и построить эту прямую на чертеже. 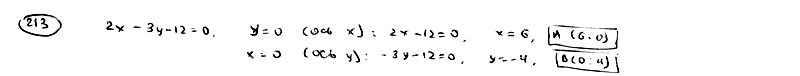 |
| | | Найти точку пересечения двух прямых 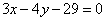 , , 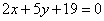 . . 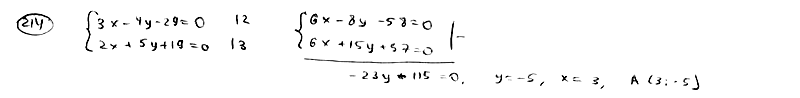 |
| | | Стороны АВ, ВС и АС треугольника АВС даны соответственно уравнениями 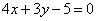 , , 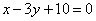 , , 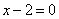 . Определить координаты его вершин. . Определить координаты его вершин. 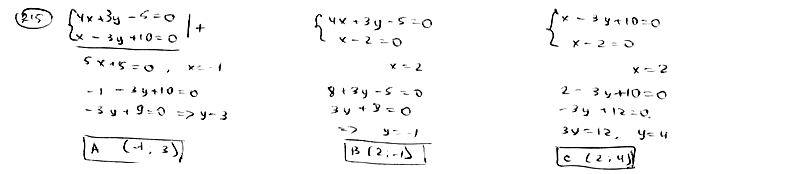 |
| | | Даны уравнения двух сторон параллелограмма 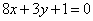 , , 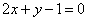 и уравнение одной из его диагоналей и уравнение одной из его диагоналей 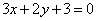 . Определить координаты вершин этого параллелограмма. . Определить координаты вершин этого параллелограмма. 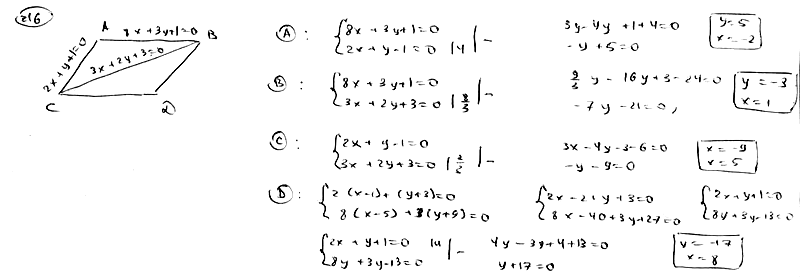 |
| | | Стороны треугольника лежат на прямых 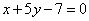 , , 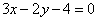 , , 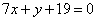 . Вычислить его площадь S. . Вычислить его площадь S. 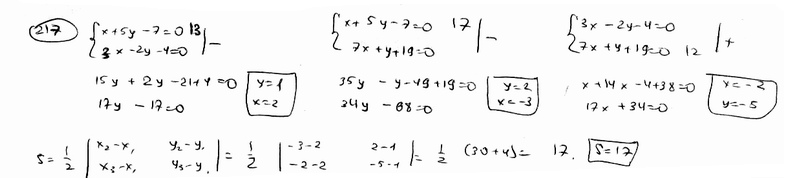 |
| | | Площадь треугольника S=8, две его вершины суть точки А(1; -2), В(2; 3), а третья вершина С лежит на прямой 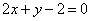 . Определить координаты вершины С. . Определить координаты вершины С. 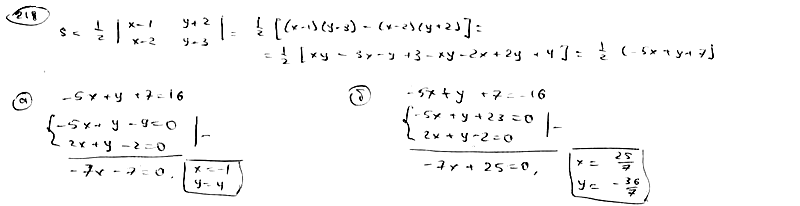 |
| | | Площадь треугольника S=1,5, две его вершины суть точки А(2; -3), В(3; -2), центр масс этого треугольника лежит на прямой 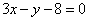 . Определить координаты третьей вершины С. . Определить координаты третьей вершины С. 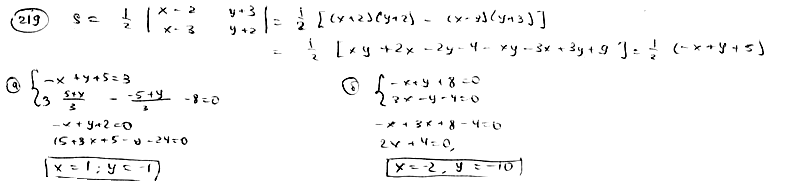 |
| | | Составить уравнение прямой и построить прямую на чертеже, зная ее угловой коэффициент k и отрезок b, отсекаемый ею на оси Oy: |
| | 220.1 | k=2/3, b=3; |
| | 220.2 | k=3, b=0; |
| | 220.3 | k=0, b=-2; |
| | 220.4 | k=-3/4, b=3; |
| | 220.5 | k=-2, b=-5; |
| | 220.6 | k=-1/3, b=2/3. 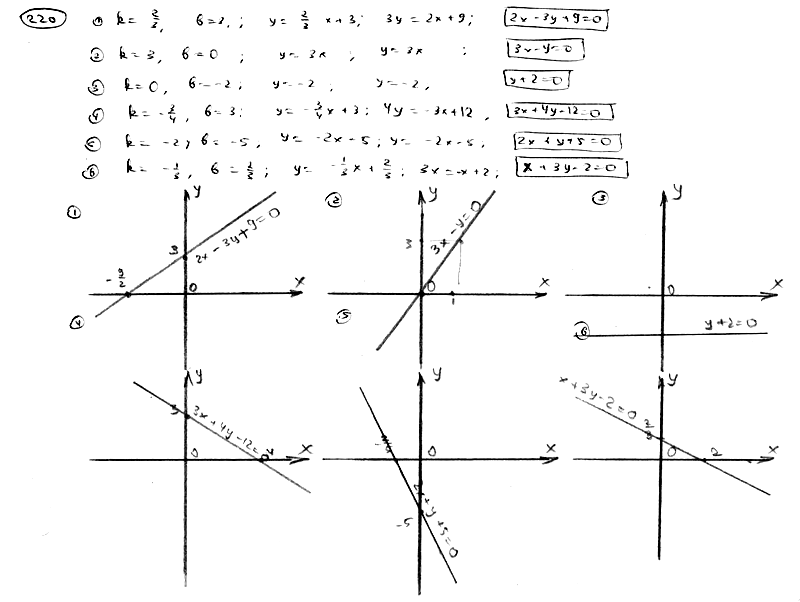 |
| | | Определить угловой коэффициент k и отрезок b, отсекаемый на оси Oy, для каждой из прямых: |
| | 221.1 | 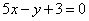 ; ; |
| | 221.2 | 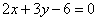 ; ; |
| | 221.3 | 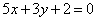 ; ; |
| | 221.4 | 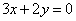 ; ; |
| | 221.5 | 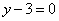 . . 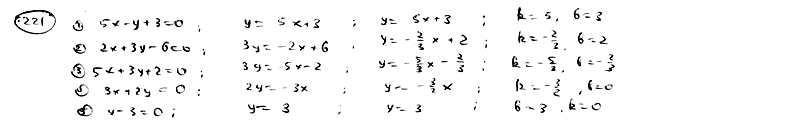 |
| | | Дана прямая 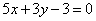 . Определить угловой коэффициент k прямой: . Определить угловой коэффициент k прямой: |
| | 222.1 | Параллельной данной прямой; |
| | 222.2 | Перпендикулярно к данной прямой.  |
| | | Дана прямая 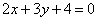 . Составить уравнение прямой, проходящей через точку М0(2; 1): . Составить уравнение прямой, проходящей через точку М0(2; 1): |
| | 223.1 | Параллельно данной прямой; |
| | 223.2 | Перпендикулярно данной прямой. 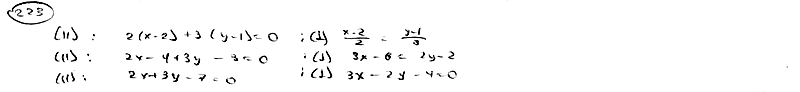 |
| | | Даны уравнения двух сторон прямоугольника 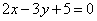 , , 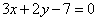 и одна из его вершин А(2; -3). Составить уравнения двух других сторон этого прямоугольника. и одна из его вершин А(2; -3). Составить уравнения двух других сторон этого прямоугольника. 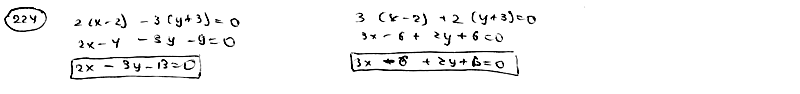 |
| | | Даны уравнения двух сторон прямоугольника 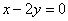 , , 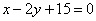 и уравнение одной из его диагоналей и уравнение одной из его диагоналей 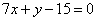 . Найти вершины прямоугольника. . Найти вершины прямоугольника. 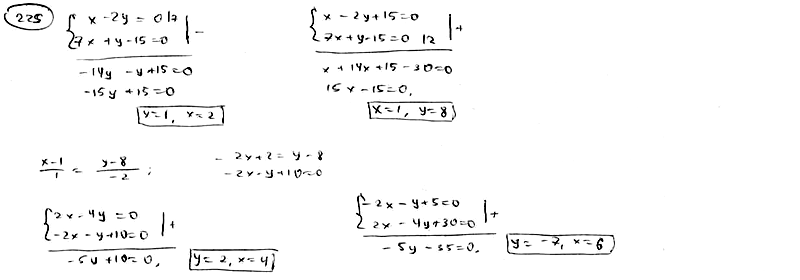 |
| | | Найти проекцию точке Р(-5; 13) относительно прямой 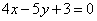 . . 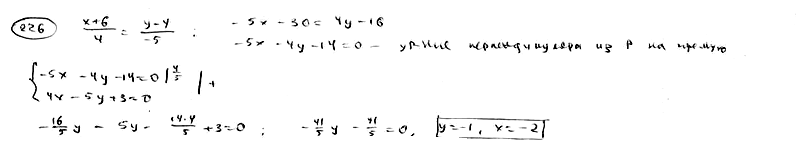 |
| | | Найти точку Q, симметричную точке Р(-5; 13) относительно прямой 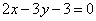 . . 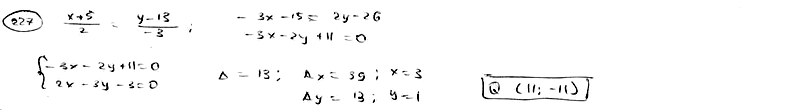 |
| | | В каждом из следующих случаев составить уравнение прямой, параллельной двум данным прямым и проходящей посередине между ними: |
| | 228.1 | 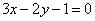 , , 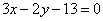 ; ; |
| | 228.2 | 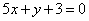 , , 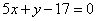 ; ; |
| | 228.3 | 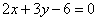 , , 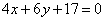 ; ; |
| | 228.4 | 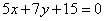 , , 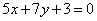 ; ; |
| | 228.5 | 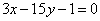 , , 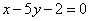 . . 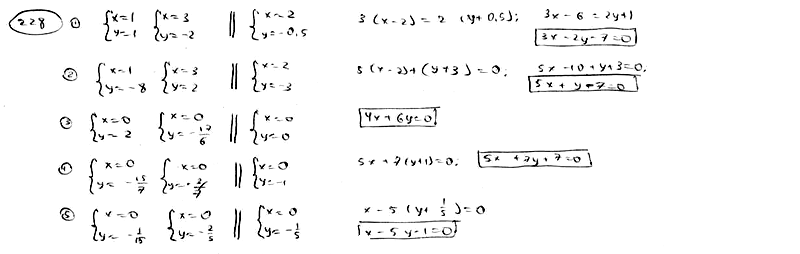 |
| | | Вычислить угловой коэффициент k прямой, проходящей через две данные точки: |
| | 229.1 | M1(2; -5), M2(3; 2); |
| | 229.2 | P(-3, 1), Q(7; 8); |
| | 229.3 | A(5; -3), B(-1; 6). 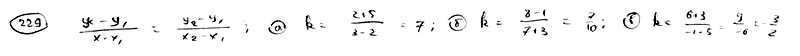 |
| | | Составить уравнения прямых, проходящих через вершины треугольника A(5; -4), B(-1; 3), C(-3; -2) параллельно противоположным сторонам. 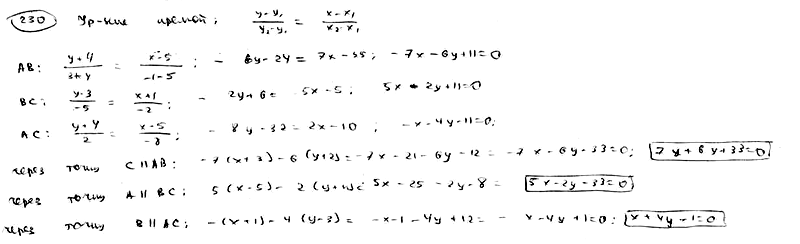 |
| | | Даны середины сторон треугольника M1(2; 1), M2(5; 3), M3(3; -4). Составить уравнение его сторон. 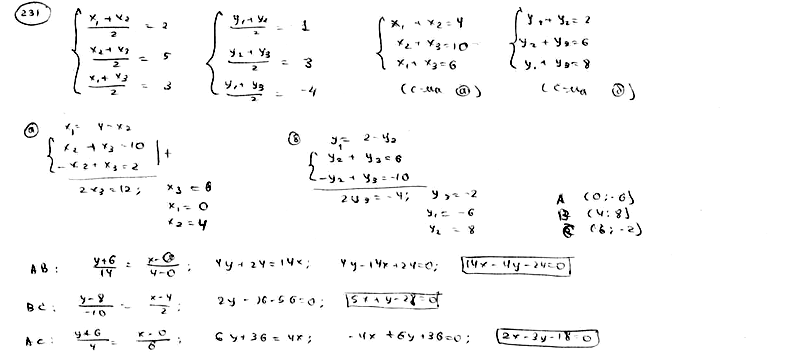 |
| | | Даны две точки P(2; 3), Q(-1; 0). Составить уравнение прямой, проходящей через точку Q перпендикулярно к отрезку 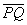 . . 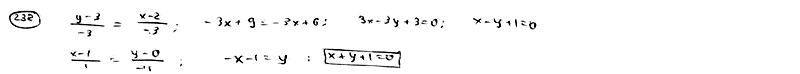 |
| | | Составить уравнение прямой, если точка P(2; 3) служит основанием перпендикуляра, опущенного из начала координат на эту прямую. 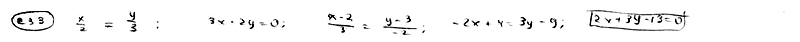 |
| | | Даны вершины треугольника M1(2; 1), M2(-1; -1), M3(3; 2). Составить уравнения его высот. 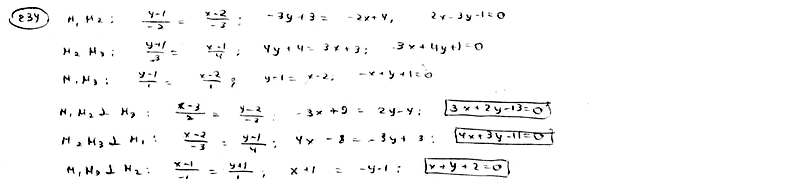 |
| | | Стороны треугольника даны уравнениями 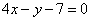 , , 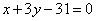 , , 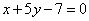 . Определить точку пересечения его высот. . Определить точку пересечения его высот. 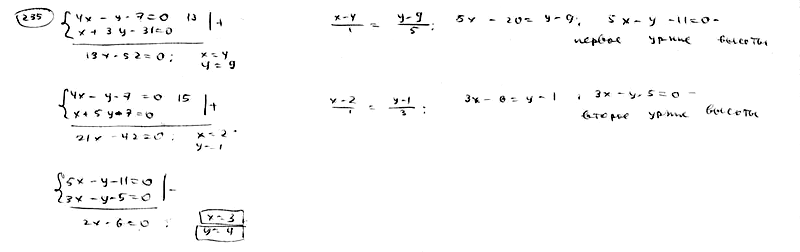 |
| | | Даны вершины треугольника A(1; -1), B(-2; 1), C(3; 5). Составить уравнение перпендикуляра, опущенного из вершины А на медиану, проведенную из вершины В. 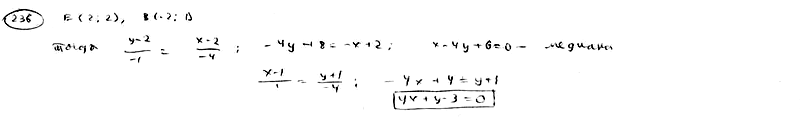 |
| | | Даны вершины треугольника A(2; -2), B(3; -5), C(5; 7). Составить уравнение перпендикуляра, опущенного из вершины С на биссектрису внутреннего угла при вершине А. 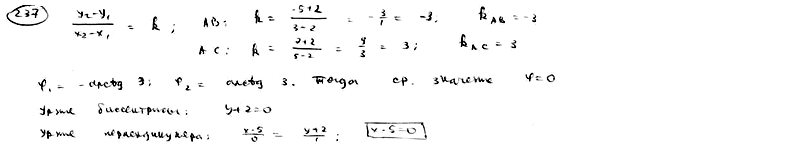 |
| | | Составить уравнения сторон и медиан треугольника с вершинами A(3; 2), B(5; -2), C(1; 0). 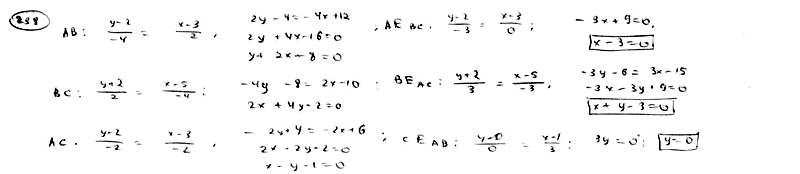 |
| | | Через точки M1(-1; 2), M2(2; 3) проведена прямая. Определить точки пересечения этой прямой с осями координат. 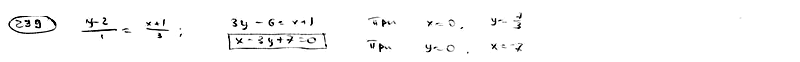 |
| | | Доказать, что условие, при котором три точки M1(x1, y1), M2(x2, y2), M3(x3, y3) лежат на одной прямой, может быть записано в следующем виде: 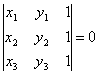 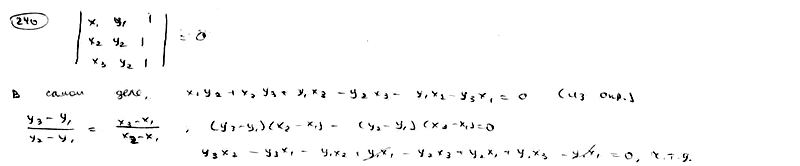 |
| | | Доказать, что уравнение прямой, проходящей через две данные точки M1(x1, y1), M2(x2, y2), может быть записано в следующем виде: 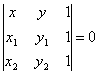 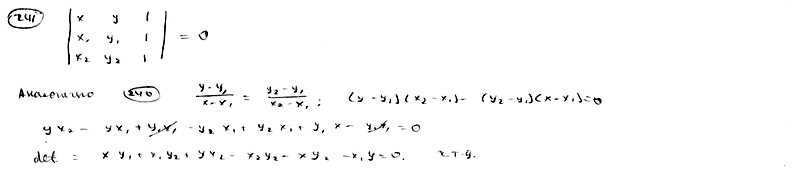 |
| | | Даны последовательные вершины выпуклого четырехугольника A(-3; 1), B(3; 9), C(7; 6), D(-2; -6). Определить точку пересечения его диагоналей. 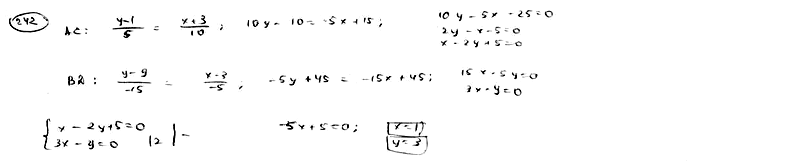 |
| | | Даны две смежные вершины A(-3; -1), B(2; 2) параллелограмма ABCD и точка Q(3; 0) пересечения его диагоналей. Составить уравнения сторон этого параллелограмма. 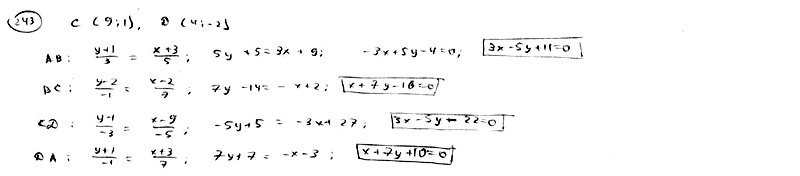 |
| | | Даны уравнения двух сторон прямоугольника 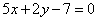 , , 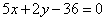 и уравнение его диагонали и уравнение его диагонали 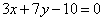 . Составить уравнения остальных сторон и второй диагонали этого прямоугольника. . Составить уравнения остальных сторон и второй диагонали этого прямоугольника. 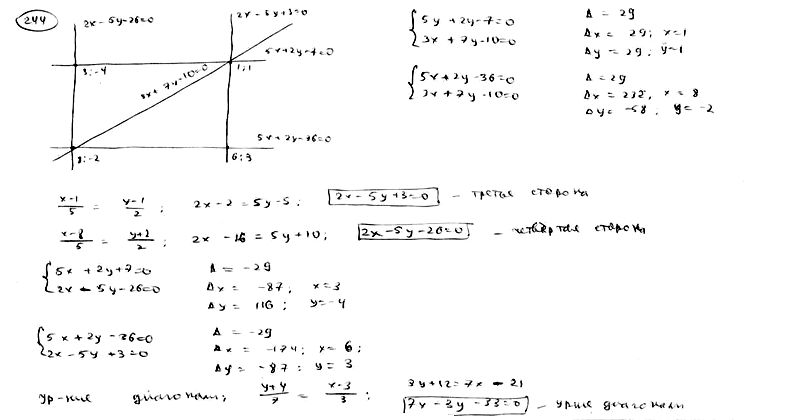 |
| | | Даны вершины треугольника A(1; -2), B(5; 4), C(-2; 0). Составить уравнения биссектрис его внутреннего и внешнего углов при вершине А. 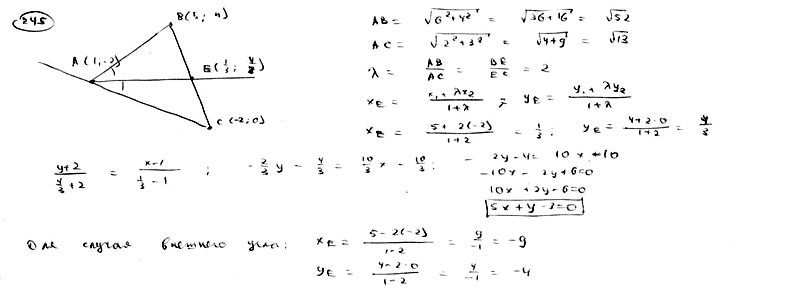 |
| | | Составить уравнение прямой, проходящей через точку P(3; 5) на одинаковых расстояниях от точек A(-7; 3) и B(11; -15). 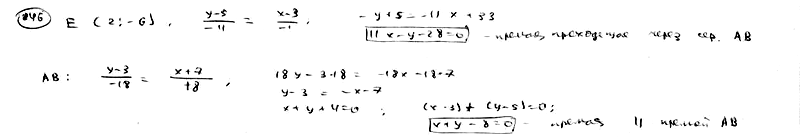 |
| | | Найти проекцию точки P(-8; 12) на прямую, проходящую через точки A(2; -3), B(-5; 1). 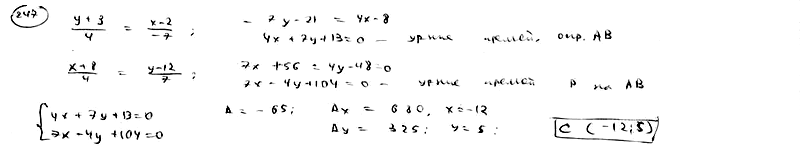 |
| | | Найти точку M1, симметричную точке М2(8; -9) относительно прямой, проходящей через точки А(3; -4), B(-1; -2). 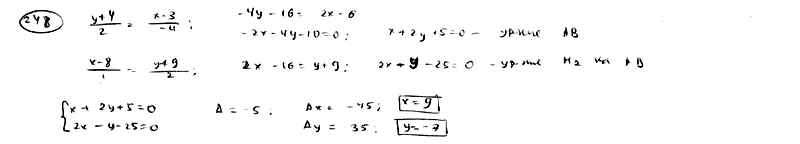 |
| | | На оси абсцисс найти такую точку P, чтобы сумма ее расстояний до точек M(1; 2), N(3; 4) была наименьшей. 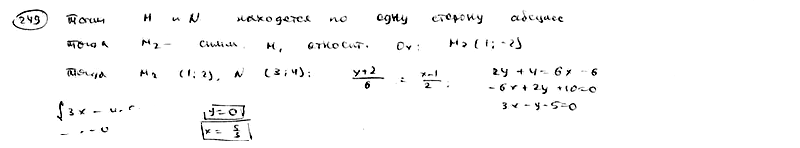 |
| | | На оси ординат найти такую точку P, чтобы сумма ее расстояний до точек M(-3; 2), N(2; 5) была наибольшей.  |
| | | На прямой 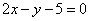 найти такую точку Р, сумма расстояний которой до точек A(-7; 1), B(-5; 5) была бы наименьшей. найти такую точку Р, сумма расстояний которой до точек A(-7; 1), B(-5; 5) была бы наименьшей. 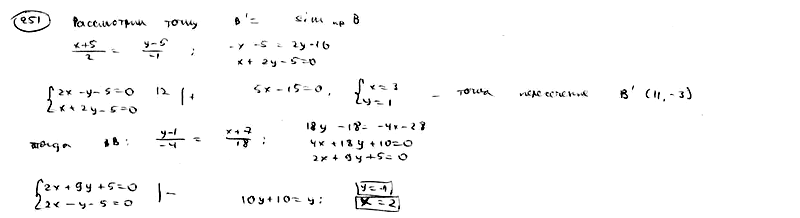 |
| | | На прямой 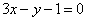 найти такую точку Р, разность расстояний которой до точек A(4; 1), B(0; 4) была бы наибольшей. найти такую точку Р, разность расстояний которой до точек A(4; 1), B(0; 4) была бы наибольшей. 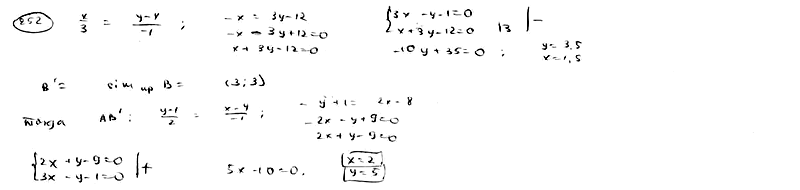 |
| | | Определить угол 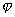 между двумя прямыми: между двумя прямыми: |
| | 253.1 | 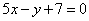 , , 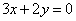 ; ; |
| | 253.2 | 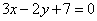 , , 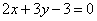 ; ; |
| | 253.3 | 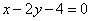 , , 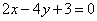 ; ; |
| | 253.4 | 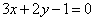 , , 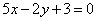 . . 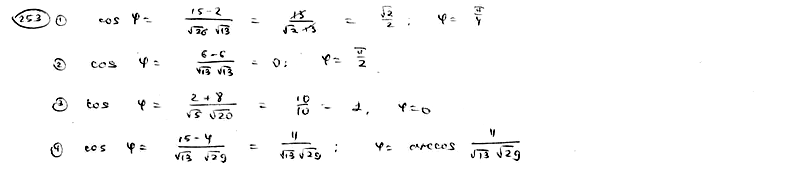 |
| | | Дана прямая 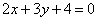 . Составить уравнение прямой, проходящей через точку M0(2; 1) под углом 450 к данной прямой. . Составить уравнение прямой, проходящей через точку M0(2; 1) под углом 450 к данной прямой. 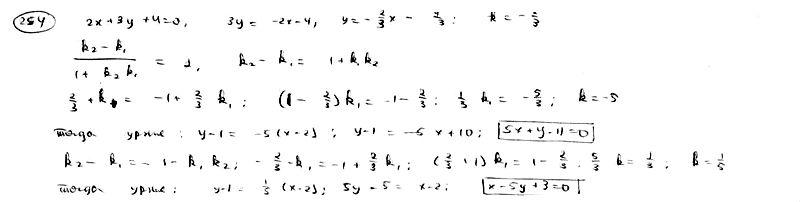 |
| | | Точка А(-4; 5) является вершиной квадрата, диагональ которого лежит на прямой 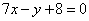 . Составить уравнения сторон и второй диагонали этого квадрата. . Составить уравнения сторон и второй диагонали этого квадрата.  |
| | | Даны две противоположные вершины квадрата A(-1; 3), C(6; 2). Составить уравнения его сторон. 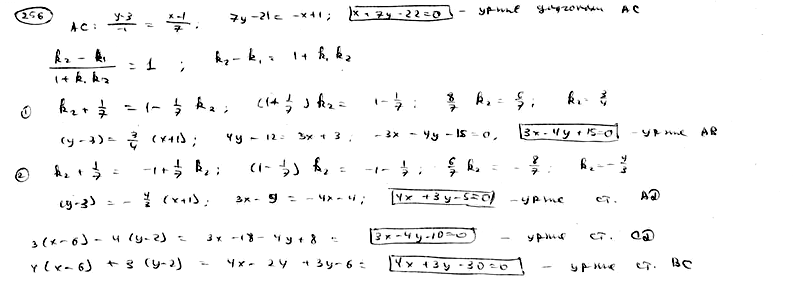 |
| | | Точка E(1; -1) является центром квадрата, одна из сторон которого лежит на прямой 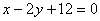 . Составить уравнения прямых, на которых лежат остальные стороны этого квадрата. . Составить уравнения прямых, на которых лежат остальные стороны этого квадрата. 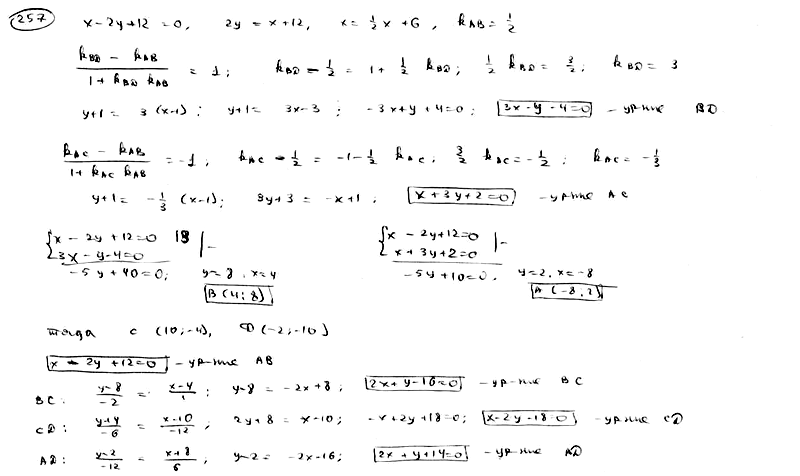 |
| | | Из точки M0(-2; 3) под углом 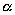 к оси Ox направлен луч света. Известно, что к оси Ox направлен луч света. Известно, что 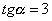 . Дойдя до оси Ox, луч от нее отразился. Составить уравнения прямых, на которых лежат падающий и отраженный лучи. . Дойдя до оси Ox, луч от нее отразился. Составить уравнения прямых, на которых лежат падающий и отраженный лучи. 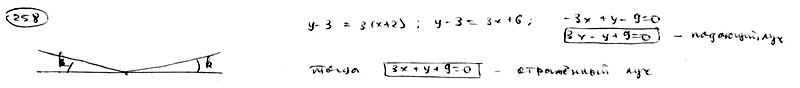 |
| | | Луч света направлен по прямой 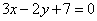 , луч от нее отразился. Составить уравнение прямой, на которой лежит отраженный луч. , луч от нее отразился. Составить уравнение прямой, на которой лежит отраженный луч. 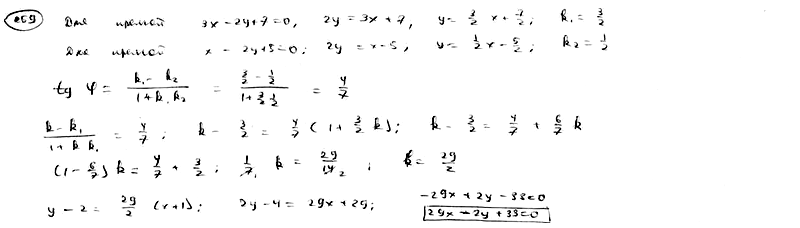 |
| | | Даны уравнения сторон треугольника 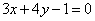 , , 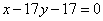 , , 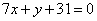 . Доказать, что этот треугольник равнобедренный. Решить задачу при помощи сравнения углов треугольника. . Доказать, что этот треугольник равнобедренный. Решить задачу при помощи сравнения углов треугольника. 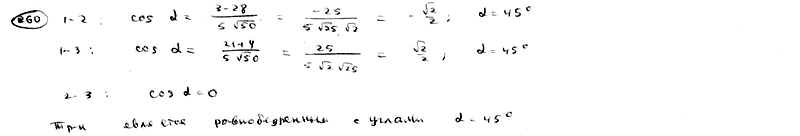 |
| | | Доказатть, что уравнение прямой, проходящей через точку M1(x1; y1) параллельно прямой 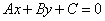 , может быть записано в виде , может быть записано в виде 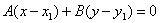 . .  |
| | | Составить уравнение прямой, проходящей через точку М1(2: -3) параллельно прямой: |
| | 262.1 | 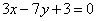 ; ; |
| | 262.2 | 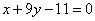 ; ; |
| | 262.3 | 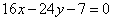 ; ; |
| | 262.4 | 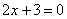 ; ; |
| | 262.5 | 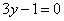 . . 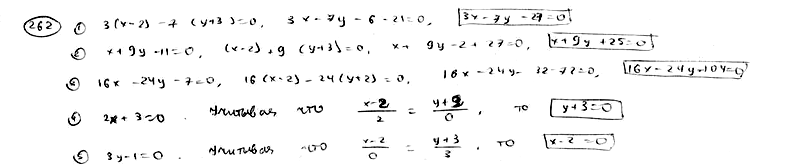 |
| | | Доказать, что условие перпендикулярности прямых 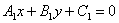 ; ; 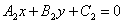 может быть записано в следующем виде: может быть записано в следующем виде: 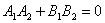 . .  |
| | | Установить, какие из следующих пар прямых перпендикулярны. Решить задачу, не вычисляя угловых коэффициентов данных прямых. |
| | 264.1 | 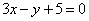 , , 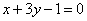 ; ; |
| | 264.2 | 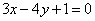 , , 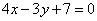 ; ; |
| | 264.3 | 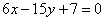 , , 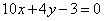 ; ; |
| | 264.4 | 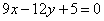 , , 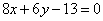 ; ; |
| | 264.5 | 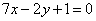 , , 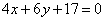 ; ; |
| | 264.6 | 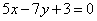 , , 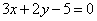 . . 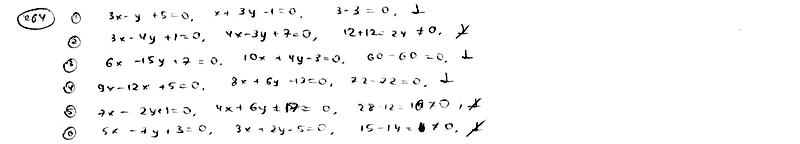 |
| | | Доказать, что формула для определения угла 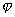 между прямыми между прямыми 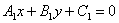 , , 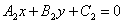 может быть записана в следующей форме: может быть записана в следующей форме: 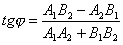  |
| | | Определить угол 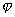 , образованный двумя прямыми. Решить задачу, не вычисляя угловых коэффициентов данных прямых. , образованный двумя прямыми. Решить задачу, не вычисляя угловых коэффициентов данных прямых. |
| | 266.1 | 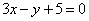 , , 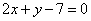 ; ; |
| | 266.2 | 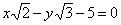 , , 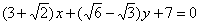 ; ; |
| | 266.3 | 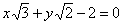 , , 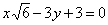 . .  |
| | | Даны две вершины треугольника M1(-10; 2), M2(6; 4); его высоты пересекаются в точке N(5; 2). Определить координаты третьей вершины M3.  |
| | | Даны две вершины A(3; -1), B(5; 7) треугольника ABC и точка N(4; -1) пересечения его высот. Составить уравнения сторон этого треугольника. 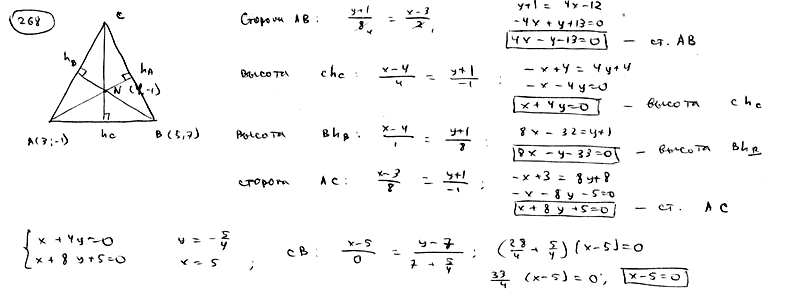 |
| | | В треугольнике АВС даны: уравнение стороны АВ: 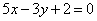 , уравнения высот АМ: , уравнения высот АМ: 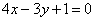 и BN: и BN: 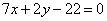 . Составить уравнения двух других сторон и третьей высоты этого треугольника. . Составить уравнения двух других сторон и третьей высоты этого треугольника. 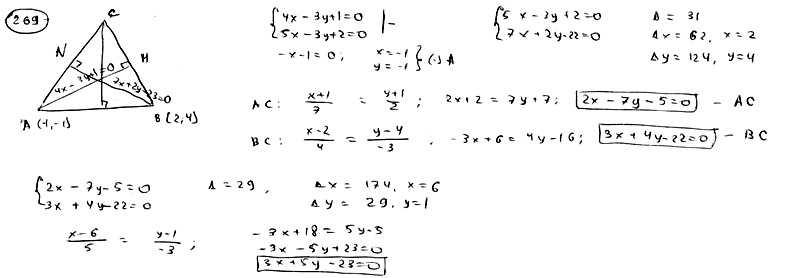 |
| | | Составить уравнения сторон треугольника АВС, если даны одна из его вершина А(1; 3) и уравнения двух медиан 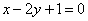 , , 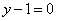 . .  |
| | | Составить уравнения сторон треугольника, сли даны одна из его вершин B(-4; -5) и уравнения двух высот 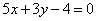 , , 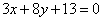 . . 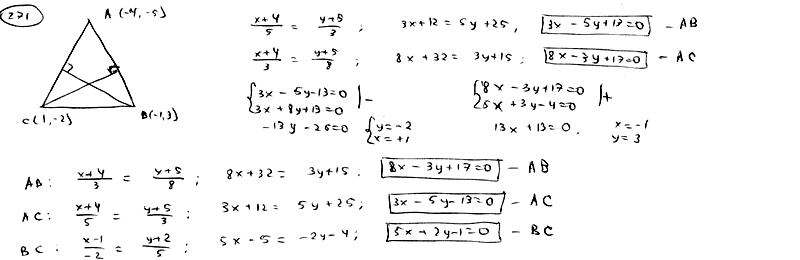 |
| | | Составить уравнения сторон треугольника, зная одну из его вершин A(4; -1) и уравнения двух биссектрис 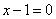 , , 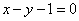 . .  |
| | | Составить уравнения сторон треугольника, зная одну из его вершин B(2; 6), а также уравнения высоты 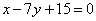 и биссектрисы и биссектрисы 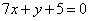 , проведенных из одной вершины. , проведенных из одной вершины.  |
| | | Составить уравнения сторон треугольника, зная одну его вершину B(2; -1), а также уравнения высоты 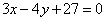 и биссектрисы и биссектрисы 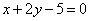 , проведенных из различных вершин. , проведенных из различных вершин.  |
| | | Составить уравнения сторон треугольника, зная одну его вершину C(4; -1), а также уравнения высоты 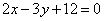 и медианы и медианы 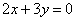 , проведенной из одной вершины. , проведенной из одной вершины.  |
| | | Составить уравнения сторон треугольника, зная одну его вершину B(2; -7), а также уравнения высоты 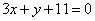 и медианы и медианы 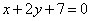 , проведенных из различных вершин. , проведенных из различных вершин. 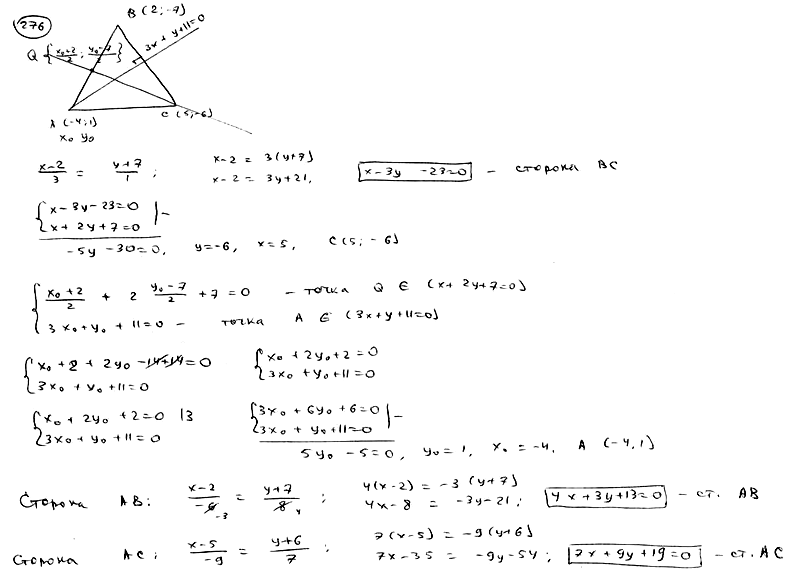 |
| | | Составить уравнения сторон треугольника, зная одну его вершину C(4; 3), а также уравнения биссектрисы 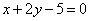 и медианы и медианы 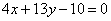 , проведенных из одной вершины. , проведенных из одной вершины. 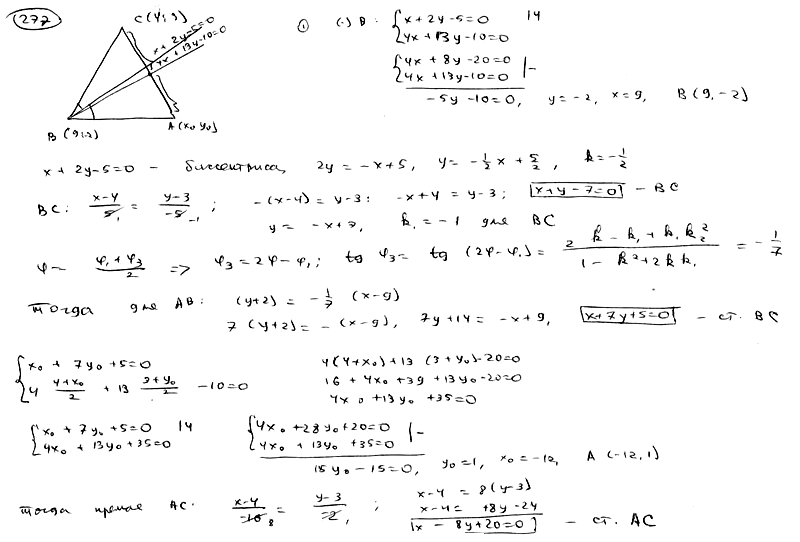 |
| | | Составить уравнения сторон треугольника, зная одну его вершину A(3; -1), а также уравнения биссектрисы 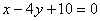 и медианы и медианы 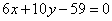 , проведенных из различных вершин. , проведенных из различных вершин. 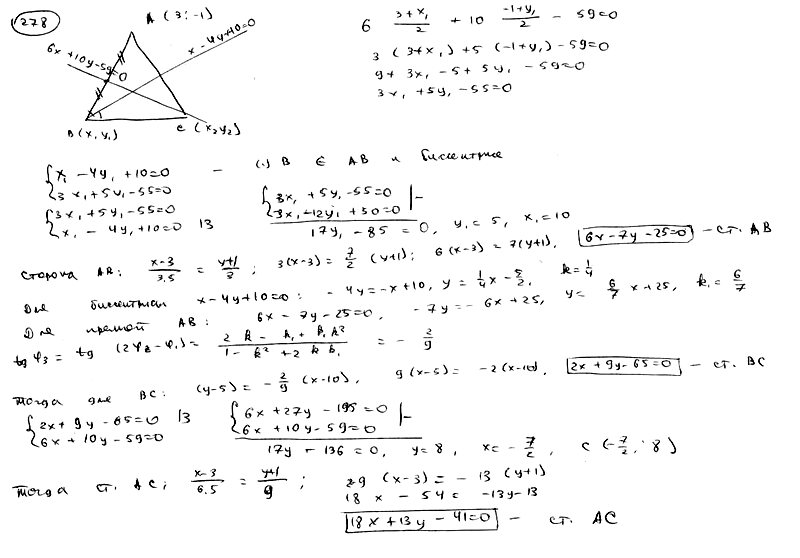 |
| | | Составить уравнение прямой, которая проходит черезначало координат и вместе с прямыми 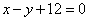 , , 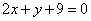 образует треугольник с площадью, равной 1,5. образует треугольник с площадью, равной 1,5.  |
| | | Среди прямых, проходящих через точку P(3; 0), найти такую, отрезок которой, заключенный между прямыми 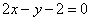 , , 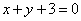 , делится в точке Р пополам. , делится в точке Р пополам. 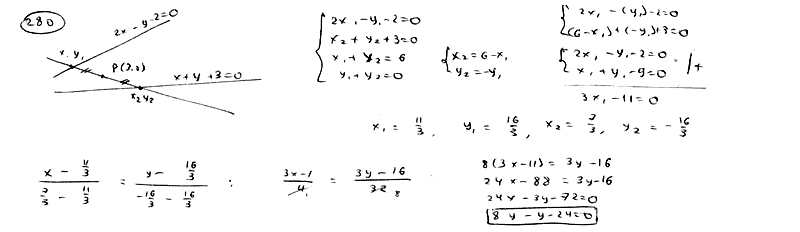 |
| | | Через точку Р(-3; -1) проведены всевозможные прямые. Доказать, что отрезок каждой из них, заключенный между прямыми 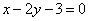 , , 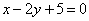 , делится в точке Р пополам. , делится в точке Р пополам.  |
| | | Через точку Р(0; 1) проведены всевозможные прямые. Доказать, что среди них нет прямой, отрезок которой, заключенный между прямыми 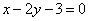 , , 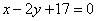 , делился бы в точке Р пополам. , делился бы в точке Р пополам. 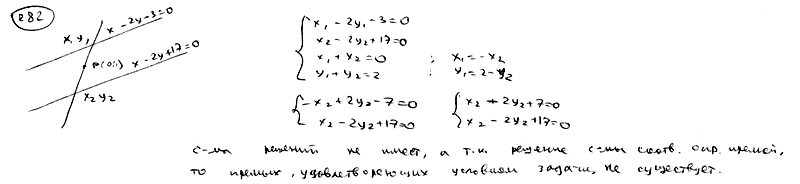 |
| | | Составить уравнение прямой, проходящей через начало координат, зная, что длина ее отрезка, заключенного между прямыми 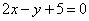 , , 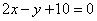 , равна , равна 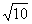 . .  |
| | | Составить уравнение прямой, проходящей через точку С(-5; 4), зная, что длина ее отрезка, заключенного между прямыми 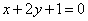 , , 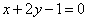 , равна 5. , равна 5.  |
Глава 13. Неполные уравнения прямой. Совместное исследование уравнений двух и трех прямых. Уравнение прямой "в отрезках"
| | | Определить, при каком значении a прямая 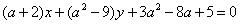 : : |
| | 285.1 | Параллельна оси абсцисс; |
| | 285.2 | Параллельна оси ординат; |
| | 285.3 | Проходит через начало координат.  |
| | | Определить, при каких значениях m и n прямая 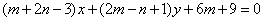 параллельна оси абсцисс и отсекает на оси ординат отрезок, равный –3 (считая от начала координат). Написать уравнение этой прямой. параллельна оси абсцисс и отсекает на оси ординат отрезок, равный –3 (считая от начала координат). Написать уравнение этой прямой. 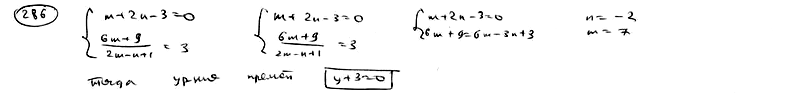 |
| | | Определить, при каких значениях m и n прямая 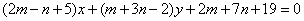 параллельна оси ординат и отсекает на оси абсцис отрезок, равный +5 (считая от начала координат). Написать уравнение этой прямой. параллельна оси ординат и отсекает на оси абсцис отрезок, равный +5 (считая от начала координат). Написать уравнение этой прямой. 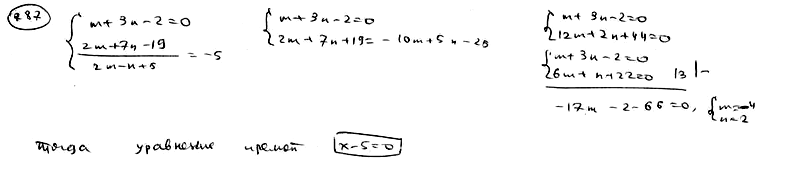 |
| | | Доказать, что в следующих случаях две данные прямые пересекаются, и найти точку их пересечения: |
| | 288.1 | 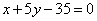 , , 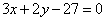 ; ; |
| | 288.2 | 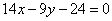 , , 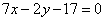 ; ; |
| | 288.3 | 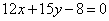 , , 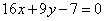 ; ; |
| | 288.4 | 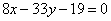 , , 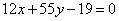 ; ; |
| | 288.5 | 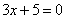 , , 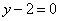 . .  |
| | | Доказать, что в следующих случаях две данные прямые параллельны: |
| | 289.1 | 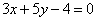 , , 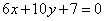 ; ; |
| | 289.2 | 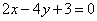 , , 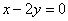 ; ; |
| | 289.3 | 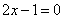 , , 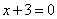 ; ; |
| | 289.4 | 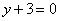 , , 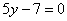 . . 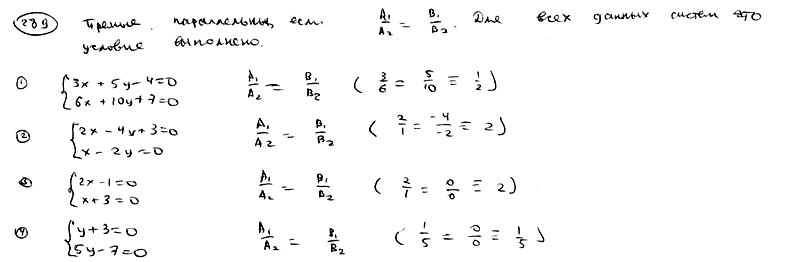 |
| | | Доказать, что в следующих случаях две данные прямые параллельны: |
| | 290.1 | 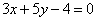 , , 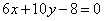 ; ; |
| | 290.2 | 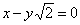 , , 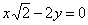 ; ; |
| | 290.3 | 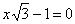 , , 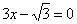 . . 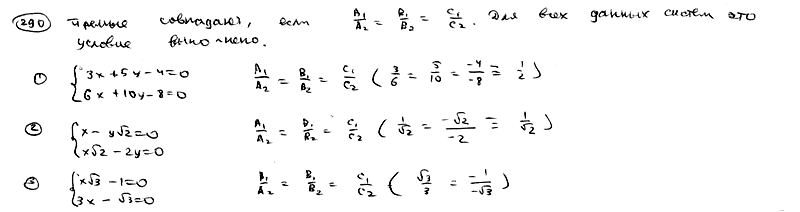 |
| | | Определить, при каких значениях a и b две прямые 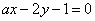 , , 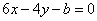 : : |
| | 291.1 | Имеют одну общую точку; |
| | 291.2 | Параллельны; |
| | 291.3 | Совпадают 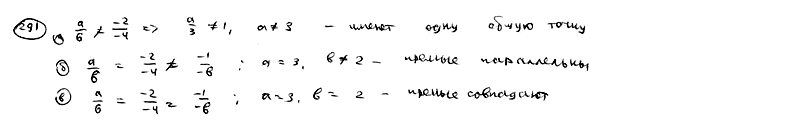 |
| | | Определить, при каких значениях m и n две прямые 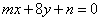 , , 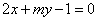 : : |
| | 292.1 | Параллельны; |
| | 292.2 | Совпадают; |
| | 292.3 | Перпендикулярны. 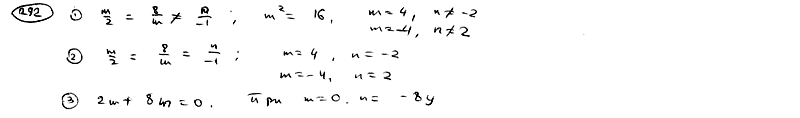 |
| | | Определить, при каком значении m две прямые 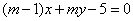 , , 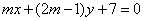 пересекаются в одной точке, лежащей на оси абсцисс. пересекаются в одной точке, лежащей на оси абсцисс.  |
| | | Определить, при каком значении m две прямые 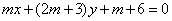 , , 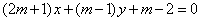 пересекаются в точке, лежающей на оси ординат. пересекаются в точке, лежающей на оси ординат. 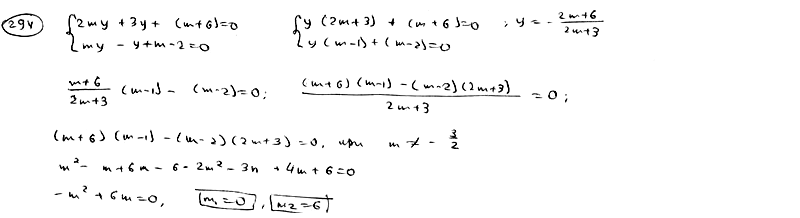 |
| | | Установить, пересекаются ли в одной точке три прямые в следующих случаях: |
| | 295.1 | 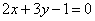 , , 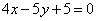 , , 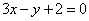 ; ; |
| | 295.2 | 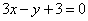 , , 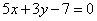 , , 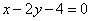 ; ; |
| | 295.3 | 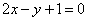 , , 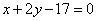 , , 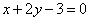 . . 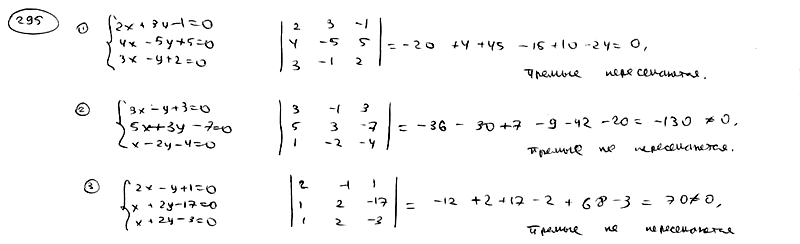 |
| | | Доказать, что если три прямые 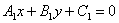 , , 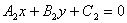 , , 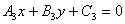 пересекаются в одной точке, то пересекаются в одной точке, то 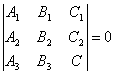 . .  |
| | | Доказать, что если 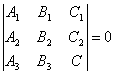 , то три прямые , то три прямые 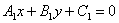 , , 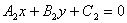 , , 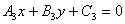 пересекаются в одной точке или параллельны. пересекаются в одной точке или параллельны.  |
| | | Определить, при каком значении а три прямые 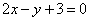 , , 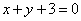 , , 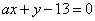 будут пересекаться в одной точке. будут пересекаться в одной точке. 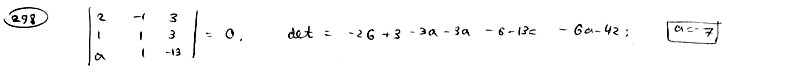 |
| | | Даны прямые. Составить для них уравнения «в отрезках» и построить эти прямые на чертеже. |
| | 299.1 | 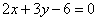 ; ; |
| | 299.2 | 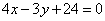 ; ; |
| | 299.3 | 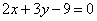 ; ; |
| | 299.4 | 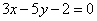 ; ; |
| | 299.5 | 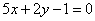 . . 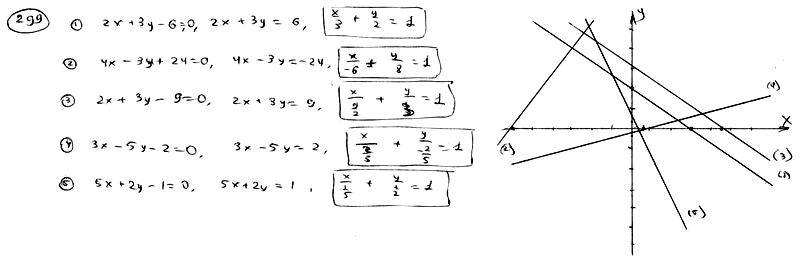 |
| | | Вычислить площадь треугольника, отсекаемого прямой 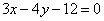 от координатного угла. от координатного угла.  |
| | | Составить уравнение прямой, которая проходит через точку M1(3; -7) и отсекает на коордиатных осях отличные от нуля отрезки одинаковой величины (считая каждый отрезок направленным от начала координат). 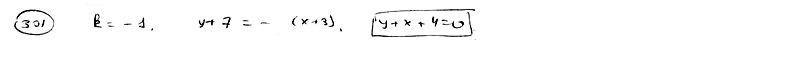 |
| | | Составить уравнение прямой, которая проходит через точку P(2; 3) и отсекает на координатных осях отрезки равной длины, считая каждый отрезок от начала координат. 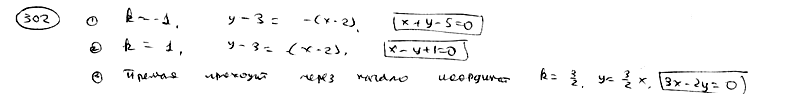 |
| | | Составить уравнение прямой, которая проходит через точку С(1; 1) и отсекает от координатного угла треугольник с площадью, равно 2. 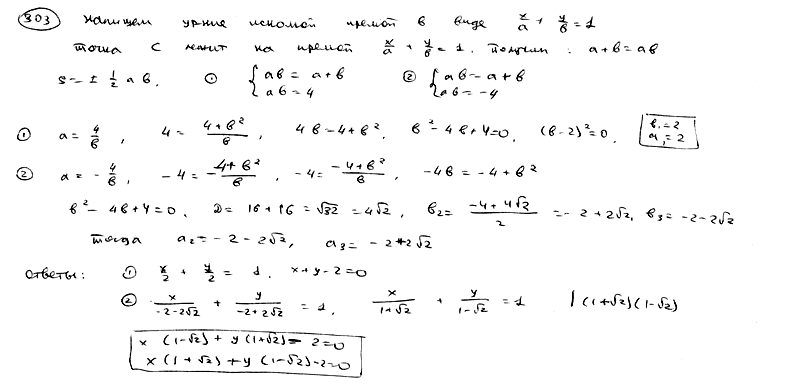 |
| | | Составить уравнение прямой, которая проходит через точку В(5; -5) и отсекает от координатного угла треугольник с площадью, равной 50.  |
| | | Составить уравнение прямой, которая проходит через точку Р(8; 6) и отсекает от координатного угла треугольник с площадью, равной 12.  |
| | | Составить уравнение прямой, которая проходит через точку Р(12; 6) и отсекает от координатного угла треугольник с площадью, равной 15. 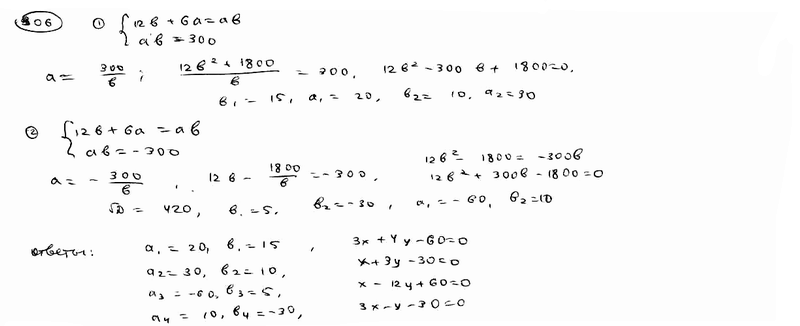 |
| | | Через точку М(4; 3) проведена прямая, отсекающая от координатного угла треугольник, площадь которого равна 3. Определить точки пересечения той прямой с осями координат. 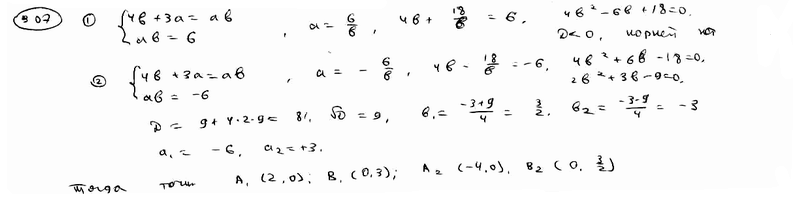 |
| | | Через точку M1(x1, y1), где x1y1>0, проведена прямая 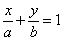 , отсекающая от координатного угла треугольник, площадь которого равна S. Определить, при каком соотношении между величинами x1, y1 и S отрезки a и b будут иметь одинаковые знаки. , отсекающая от координатного угла треугольник, площадь которого равна S. Определить, при каком соотношении между величинами x1, y1 и S отрезки a и b будут иметь одинаковые знаки. 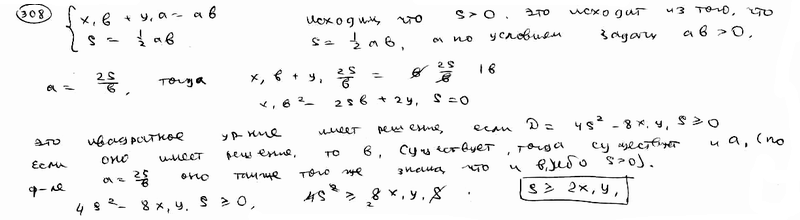 |
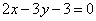 и какие на ней не лежат.
и какие на ней не лежат. 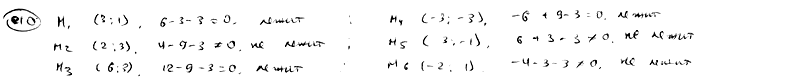
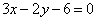 ; их абсциссы соответственно равны числам 4; 0; 2; -2; -6. Определить ординаты этих точек.
; их абсциссы соответственно равны числам 4; 0; 2; -2; -6. Определить ординаты этих точек. 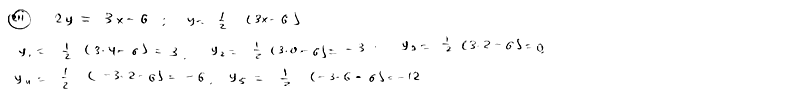
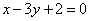 ; их ординаты соответственно равны числам 1; 0; 2; -1, 3. Определить абсциссы этих точек.
; их ординаты соответственно равны числам 1; 0; 2; -1, 3. Определить абсциссы этих точек. 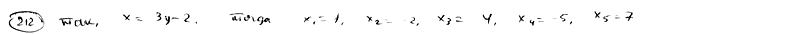
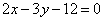 с координатными осями и построить эту прямую на чертеже.
с координатными осями и построить эту прямую на чертеже. 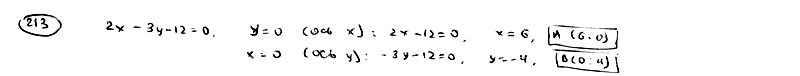
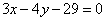 ,
, 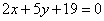 .
. 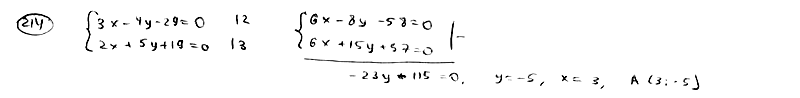
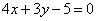 ,
, 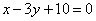 ,
, 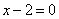 . Определить координаты его вершин.
. Определить координаты его вершин. 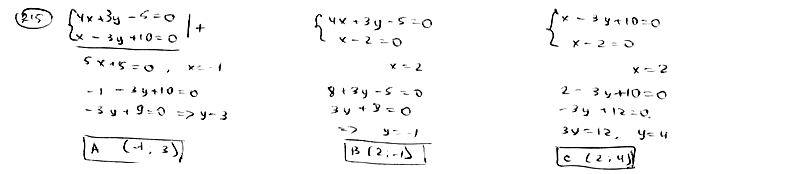
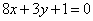 ,
, 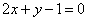 и уравнение одной из его диагоналей
и уравнение одной из его диагоналей 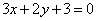 . Определить координаты вершин этого параллелограмма.
. Определить координаты вершин этого параллелограмма. 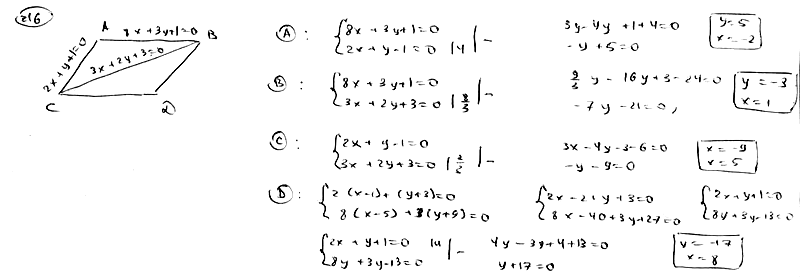
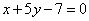 ,
, 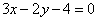 ,
, 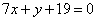 . Вычислить его площадь S.
. Вычислить его площадь S. 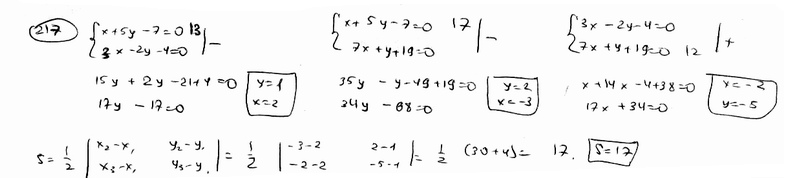
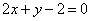 . Определить координаты вершины С.
. Определить координаты вершины С. 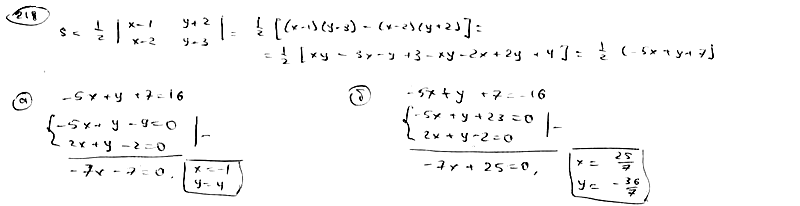
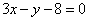 . Определить координаты третьей вершины С.
. Определить координаты третьей вершины С. 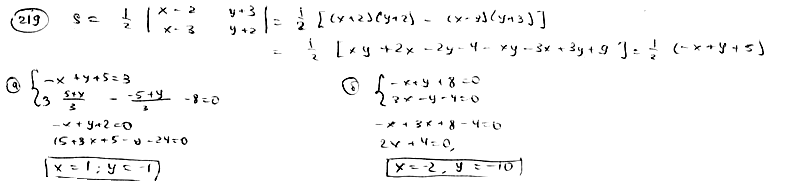

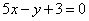 ;
; 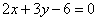 ;
; 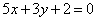 ;
; 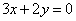 ;
; 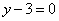 .
. 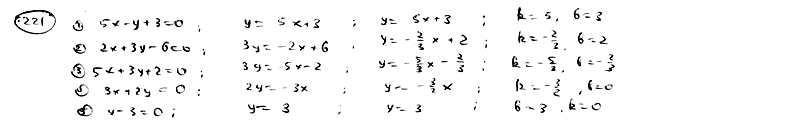
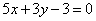 . Определить угловой коэффициент k прямой:
. Определить угловой коэффициент k прямой: 
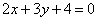 . Составить уравнение прямой, проходящей через точку М0(2; 1):
. Составить уравнение прямой, проходящей через точку М0(2; 1): 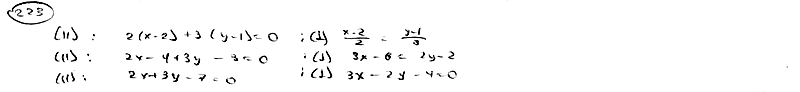
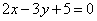 ,
, 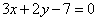 и одна из его вершин А(2; -3). Составить уравнения двух других сторон этого прямоугольника.
и одна из его вершин А(2; -3). Составить уравнения двух других сторон этого прямоугольника. 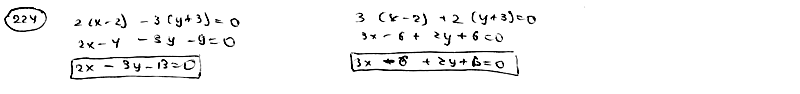
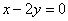 ,
, 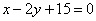 и уравнение одной из его диагоналей
и уравнение одной из его диагоналей 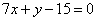 . Найти вершины прямоугольника.
. Найти вершины прямоугольника. 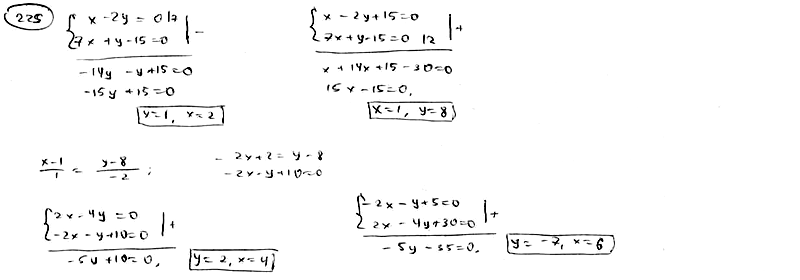
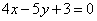 .
. 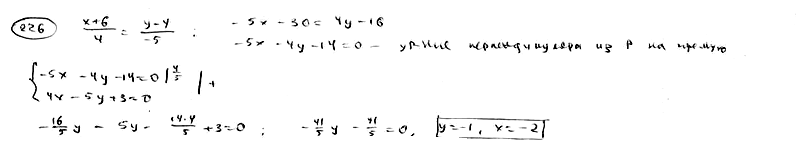
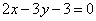 .
. 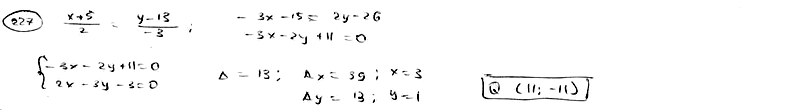
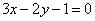 ,
, 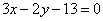 ;
; 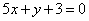 ,
, 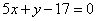 ;
; 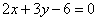 ,
, 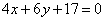 ;
; 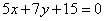 ,
, 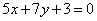 ;
; 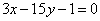 ,
, 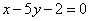 .
. 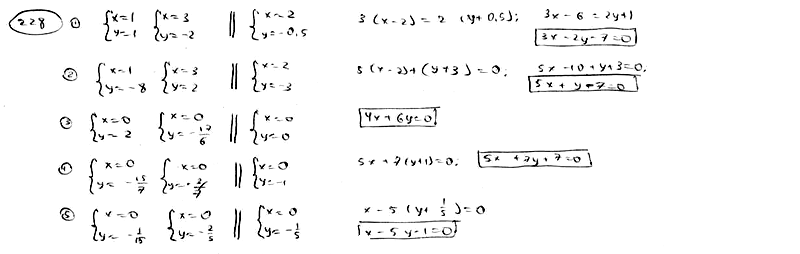
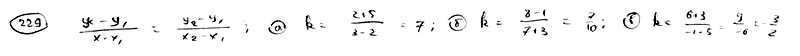
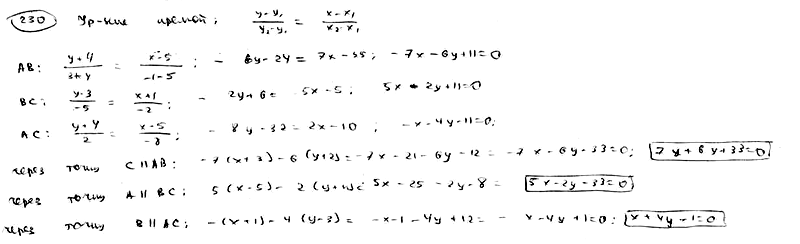
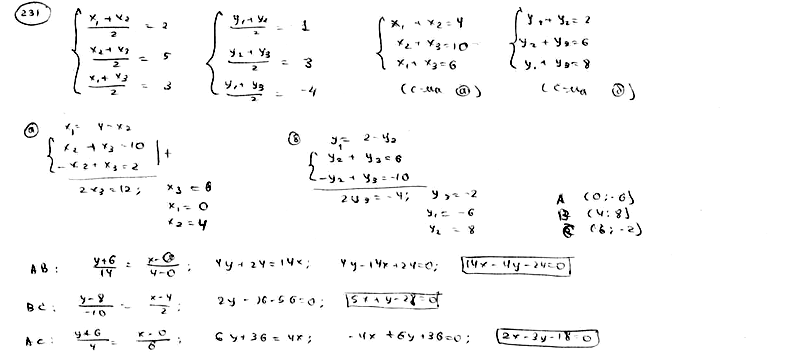
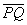 .
. 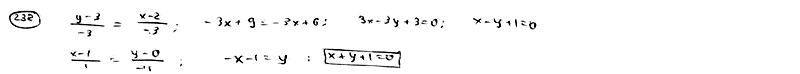
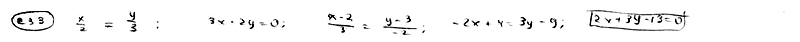
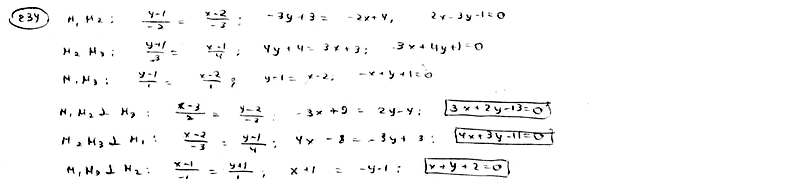
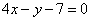 ,
, 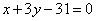 ,
, 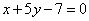 . Определить точку пересечения его высот.
. Определить точку пересечения его высот. 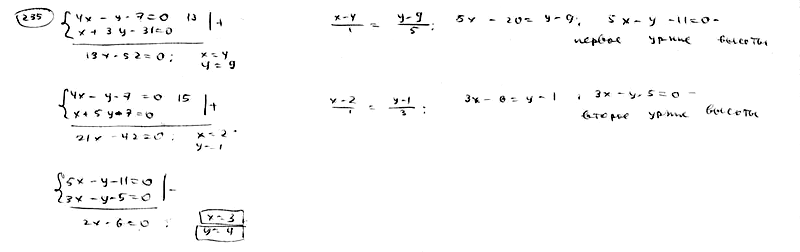
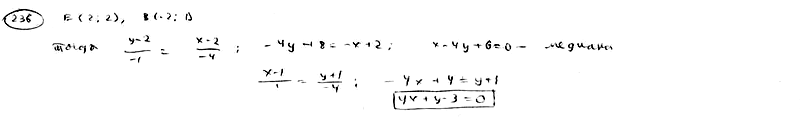
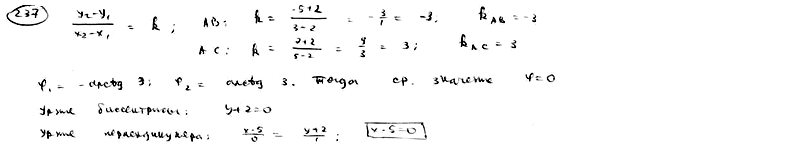
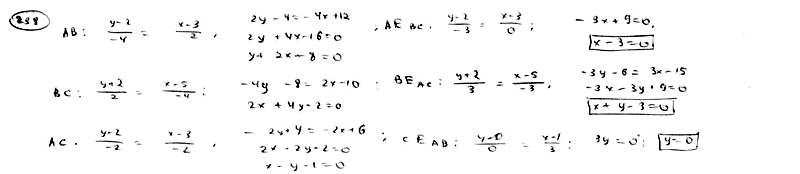
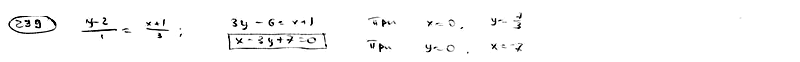
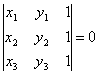
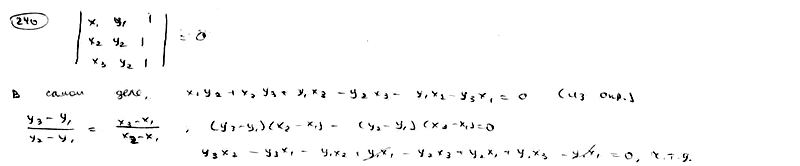
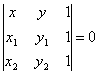
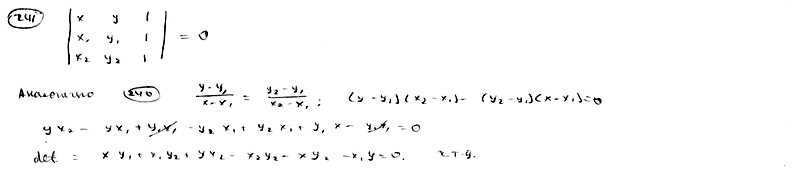
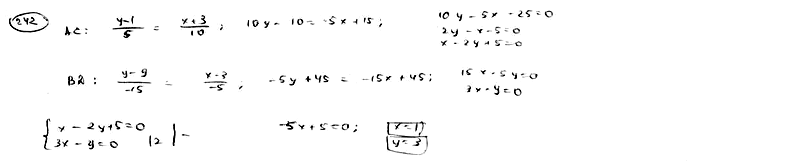
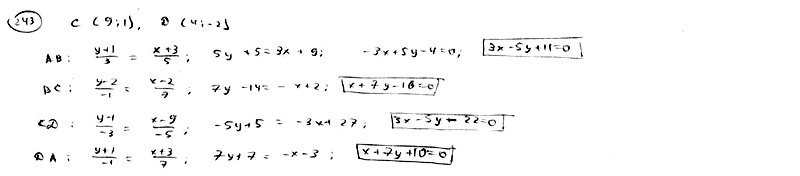
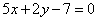 ,
, 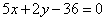 и уравнение его диагонали
и уравнение его диагонали 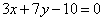 . Составить уравнения остальных сторон и второй диагонали этого прямоугольника.
. Составить уравнения остальных сторон и второй диагонали этого прямоугольника. 
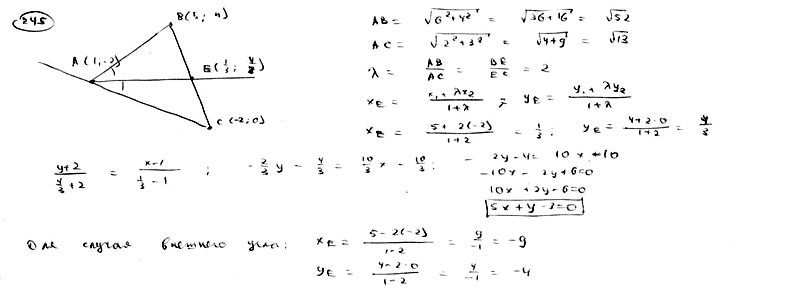
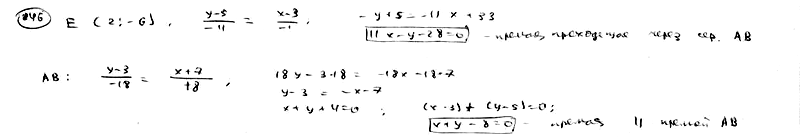
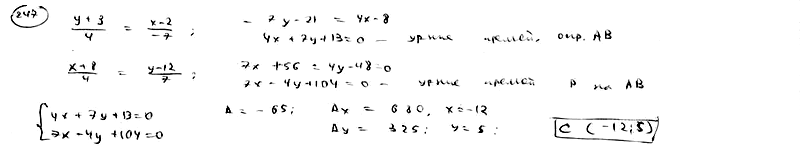
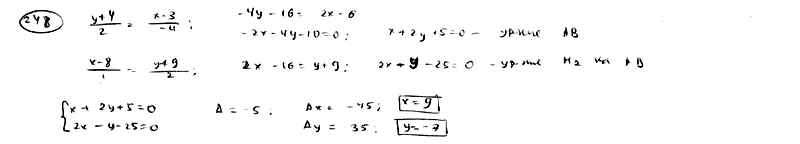
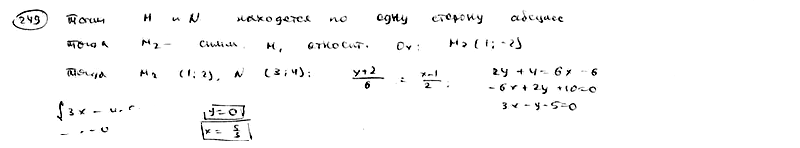

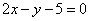 найти такую точку Р, сумма расстояний которой до точек A(-7; 1), B(-5; 5) была бы наименьшей.
найти такую точку Р, сумма расстояний которой до точек A(-7; 1), B(-5; 5) была бы наименьшей. 
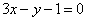 найти такую точку Р, разность расстояний которой до точек A(4; 1), B(0; 4) была бы наибольшей.
найти такую точку Р, разность расстояний которой до точек A(4; 1), B(0; 4) была бы наибольшей. 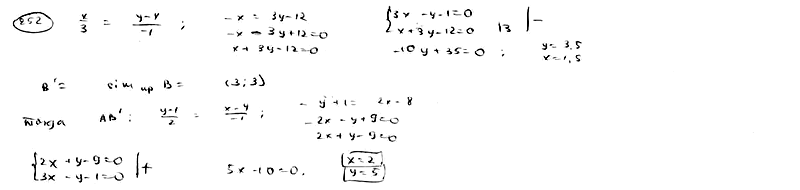
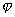 между двумя прямыми:
между двумя прямыми: 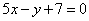 ,
, 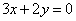 ;
; 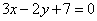 ,
, 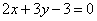 ;
; 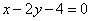 ,
, 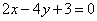 ;
; 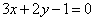 ,
, 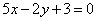 .
. 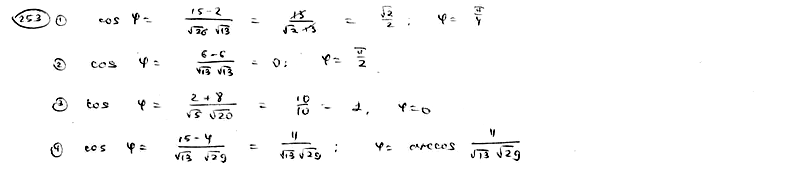
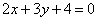 . Составить уравнение прямой, проходящей через точку M0(2; 1) под углом 450 к данной прямой.
. Составить уравнение прямой, проходящей через точку M0(2; 1) под углом 450 к данной прямой. 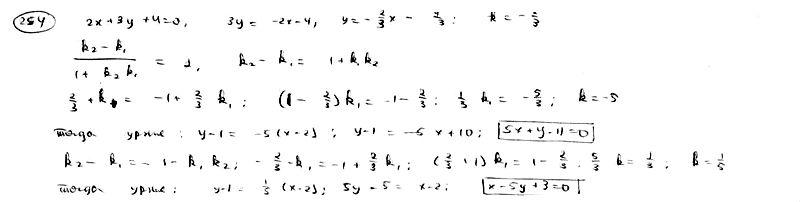
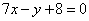 . Составить уравнения сторон и второй диагонали этого квадрата.
. Составить уравнения сторон и второй диагонали этого квадрата. 
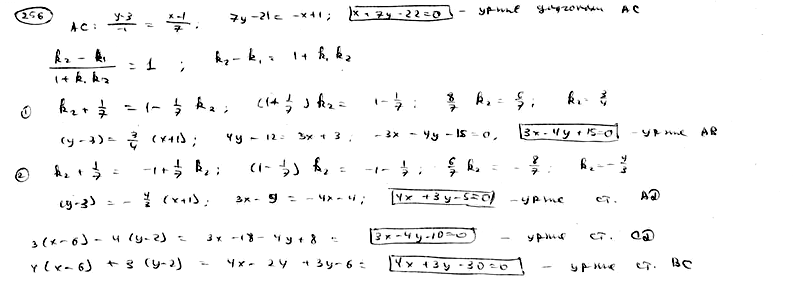
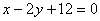 . Составить уравнения прямых, на которых лежат остальные стороны этого квадрата.
. Составить уравнения прямых, на которых лежат остальные стороны этого квадрата. 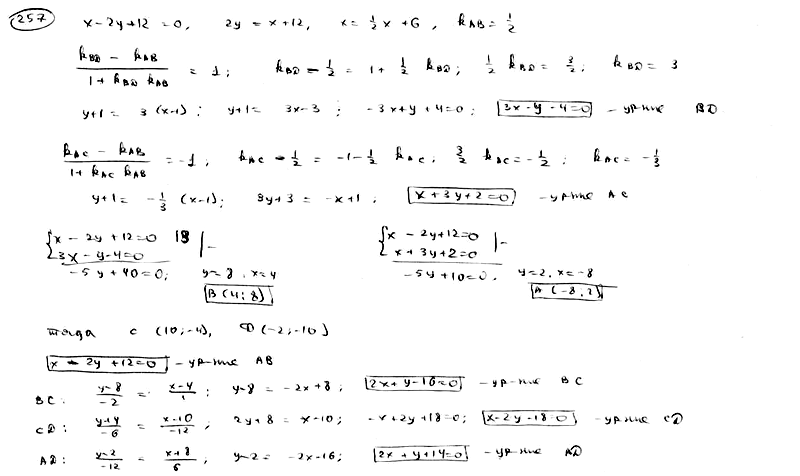
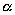 к оси Ox направлен луч света. Известно, что
к оси Ox направлен луч света. Известно, что 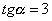 . Дойдя до оси Ox, луч от нее отразился. Составить уравнения прямых, на которых лежат падающий и отраженный лучи.
. Дойдя до оси Ox, луч от нее отразился. Составить уравнения прямых, на которых лежат падающий и отраженный лучи. 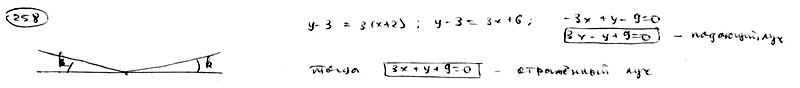
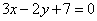 , луч от нее отразился. Составить уравнение прямой, на которой лежит отраженный луч.
, луч от нее отразился. Составить уравнение прямой, на которой лежит отраженный луч. 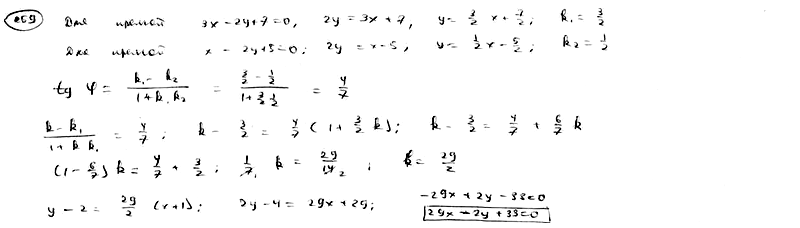
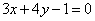 ,
, 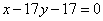 ,
, 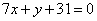 . Доказать, что этот треугольник равнобедренный. Решить задачу при помощи сравнения углов треугольника.
. Доказать, что этот треугольник равнобедренный. Решить задачу при помощи сравнения углов треугольника. 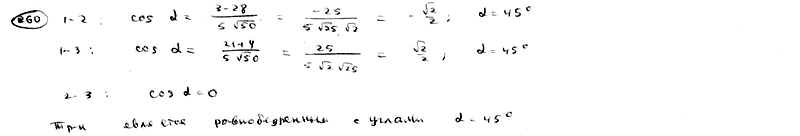
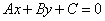 , может быть записано в виде
, может быть записано в виде 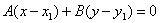 .
. 
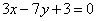 ;
; 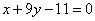 ;
; 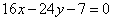 ;
; 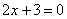 ;
; 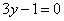 .
. 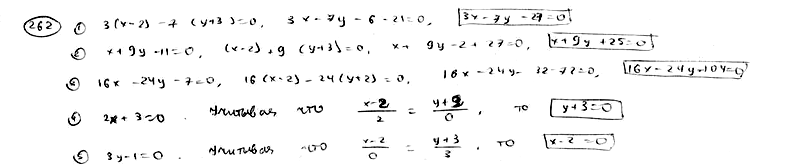
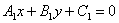 ;
; 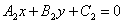 может быть записано в следующем виде:
может быть записано в следующем виде: 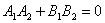 .
. 
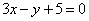 ,
, 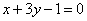 ;
; 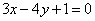 ,
, 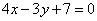 ;
; 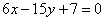 ,
, 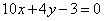 ;
; 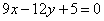 ,
, 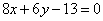 ;
; 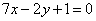 ,
, 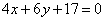 ;
; 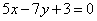 ,
, 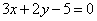 .
. 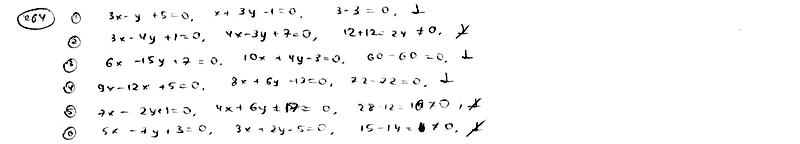
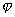 между прямыми
между прямыми 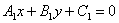 ,
, 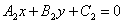 может быть записана в следующей форме:
может быть записана в следующей форме: 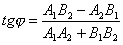

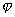 , образованный двумя прямыми. Решить задачу, не вычисляя угловых коэффициентов данных прямых.
, образованный двумя прямыми. Решить задачу, не вычисляя угловых коэффициентов данных прямых. 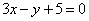 ,
, 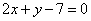 ;
; 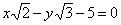 ,
, 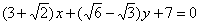 ;
; 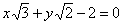 ,
, 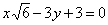 .
. 

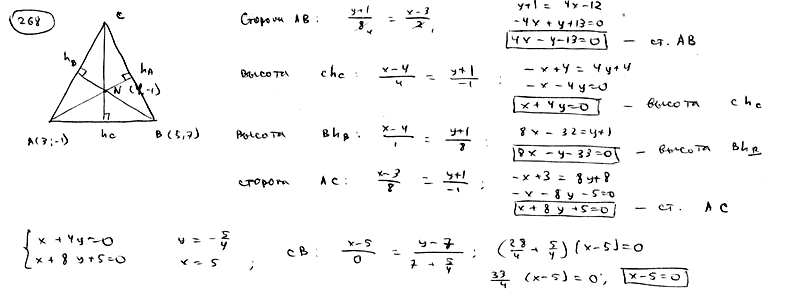
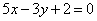 , уравнения высот АМ:
, уравнения высот АМ: 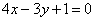 и BN:
и BN: 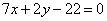 . Составить уравнения двух других сторон и третьей высоты этого треугольника.
. Составить уравнения двух других сторон и третьей высоты этого треугольника. 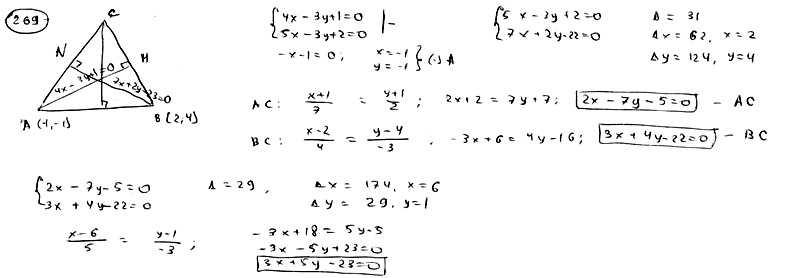
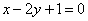 ,
, 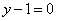 .
. 
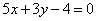 ,
, 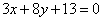 .
. 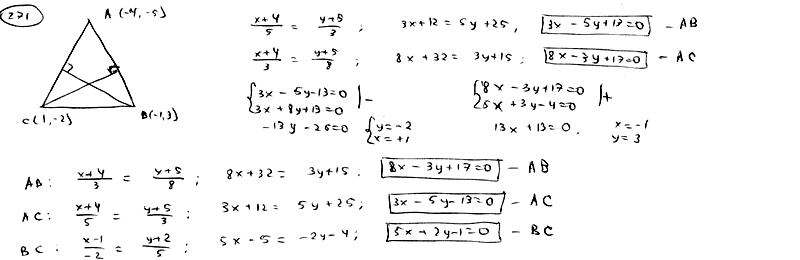
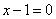 ,
, 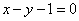 .
. 
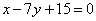 и биссектрисы
и биссектрисы 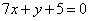 , проведенных из одной вершины.
, проведенных из одной вершины. 
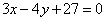 и биссектрисы
и биссектрисы 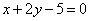 , проведенных из различных вершин.
, проведенных из различных вершин. 
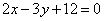 и медианы
и медианы 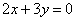 , проведенной из одной вершины.
, проведенной из одной вершины. 
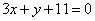 и медианы
и медианы 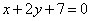 , проведенных из различных вершин.
, проведенных из различных вершин. 
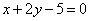 и медианы
и медианы 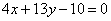 , проведенных из одной вершины.
, проведенных из одной вершины. 
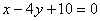 и медианы
и медианы 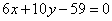 , проведенных из различных вершин.
, проведенных из различных вершин. 
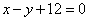 ,
, 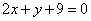 образует треугольник с площадью, равной 1,5.
образует треугольник с площадью, равной 1,5. 
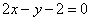 ,
,  , делится в точке Р пополам.
, делится в точке Р пополам. 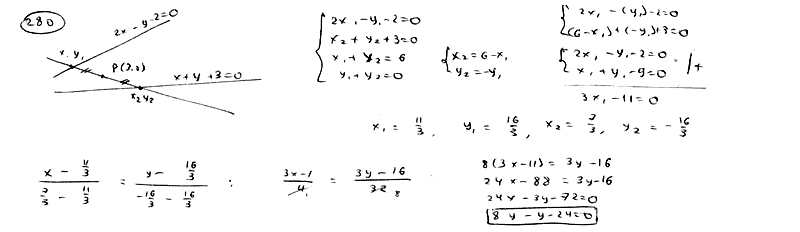
 ,
,  , делится в точке Р пополам.
, делится в точке Р пополам. 
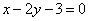 ,
, 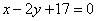 , делился бы в точке Р пополам.
, делился бы в точке Р пополам. 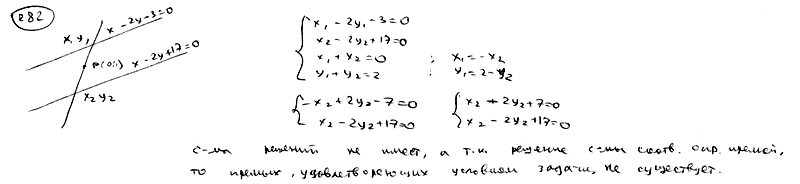
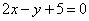 ,
, 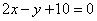 , равна
, равна 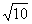 .
. 
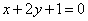 ,
, 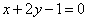 , равна 5.
, равна 5. 
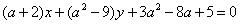 :
: 
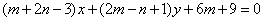 параллельна оси абсцисс и отсекает на оси ординат отрезок, равный –3 (считая от начала координат). Написать уравнение этой прямой.
параллельна оси абсцисс и отсекает на оси ординат отрезок, равный –3 (считая от начала координат). Написать уравнение этой прямой. 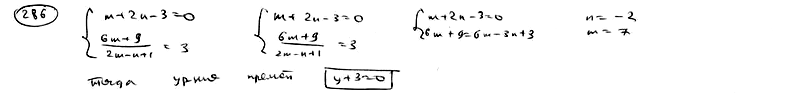
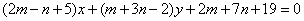 параллельна оси ординат и отсекает на оси абсцис отрезок, равный +5 (считая от начала координат). Написать уравнение этой прямой.
параллельна оси ординат и отсекает на оси абсцис отрезок, равный +5 (считая от начала координат). Написать уравнение этой прямой. 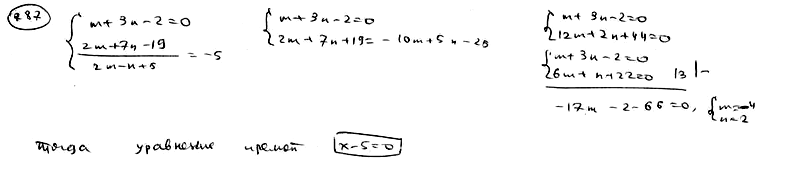
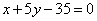 ,
, 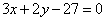 ;
; 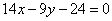 ,
, 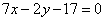 ;
; 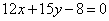 ,
, 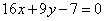 ;
; 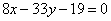 ,
, 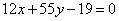 ;
; 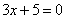 ,
, 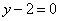 .
. 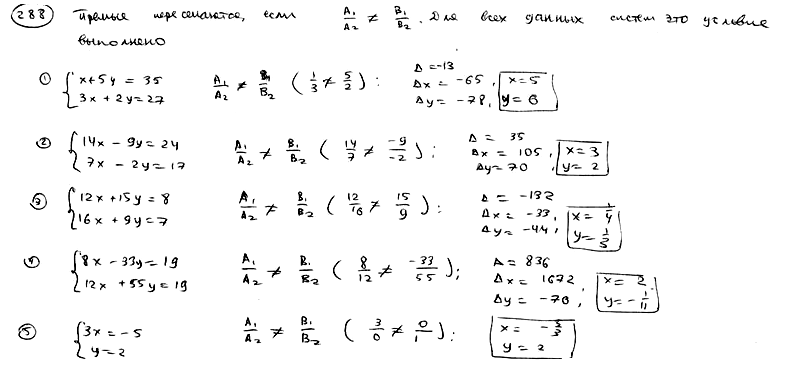
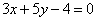 ,
, 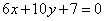 ;
; 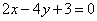 ,
, 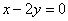 ;
; 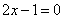 ,
, 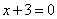 ;
; 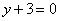 ,
, 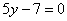 .
. 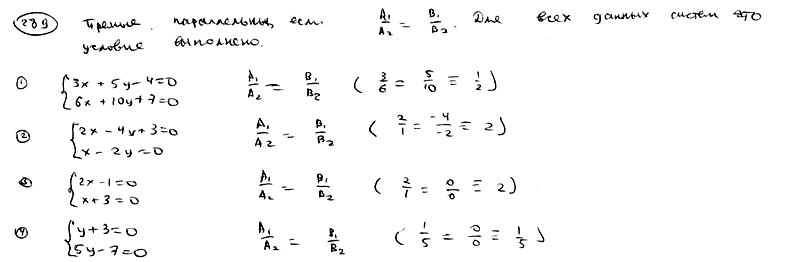
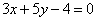 ,
, 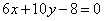 ;
; 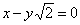 ,
, 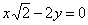 ;
; 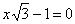 ,
, 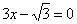 .
. 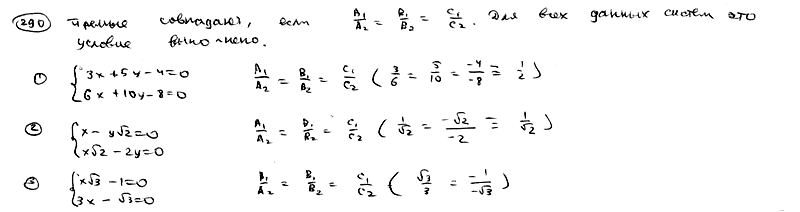
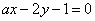 ,
, 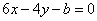 :
: 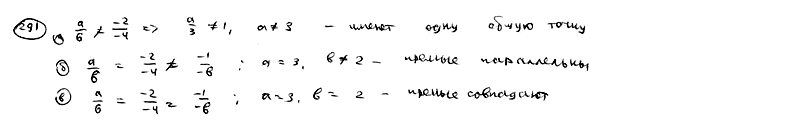
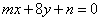 ,
, 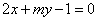 :
: 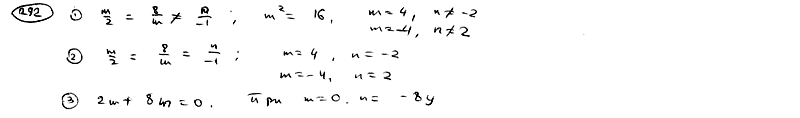
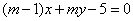 ,
, 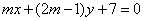 пересекаются в одной точке, лежащей на оси абсцисс.
пересекаются в одной точке, лежащей на оси абсцисс. 
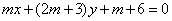 ,
, 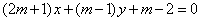 пересекаются в точке, лежающей на оси ординат.
пересекаются в точке, лежающей на оси ординат. 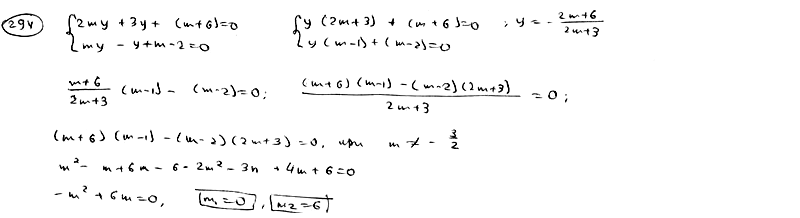
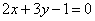 ,
, 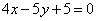 ,
, 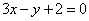 ;
; 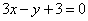 ,
, 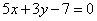 ,
, 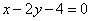 ;
; 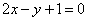 ,
, 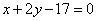 ,
, 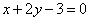 .
. 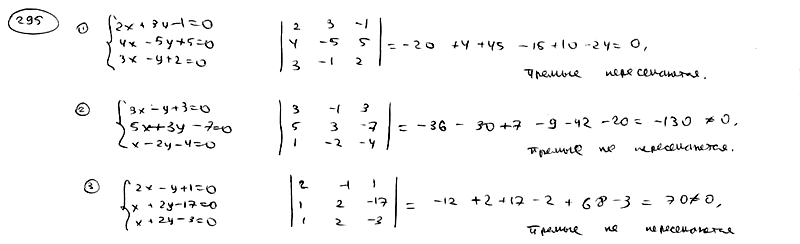
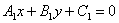 ,
, 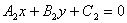 ,
, 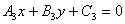 пересекаются в одной точке, то
пересекаются в одной точке, то 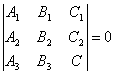 .
. 
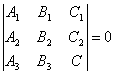 , то три прямые
, то три прямые 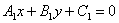 ,
, 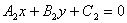 ,
, 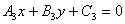 пересекаются в одной точке или параллельны.
пересекаются в одной точке или параллельны. 
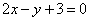 ,
, 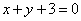 ,
, 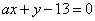 будут пересекаться в одной точке.
будут пересекаться в одной точке. 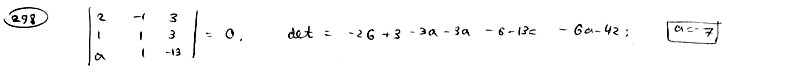
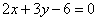 ;
; 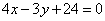 ;
; 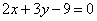 ;
; 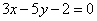 ;
; 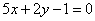 .
. 
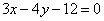 от координатного угла.
от координатного угла. 
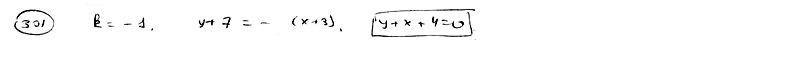


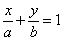 , отсекающая от координатного угла треугольник, площадь которого равна S. Определить, при каком соотношении между величинами x1, y1 и S отрезки a и b будут иметь одинаковые знаки.
, отсекающая от координатного угла треугольник, площадь которого равна S. Определить, при каком соотношении между величинами x1, y1 и S отрезки a и b будут иметь одинаковые знаки.