Доверительные оценки при равноточных измерениях

СОДЕРЖАНИЕ

		стр.
	ВВЕДЕНИЕ
1.	Оценки истинного значения измеряемой величины
1.1.	Понятие о типах оценок и их свойства
1.2.	Точечные оценки
1.3.	Доверительные оценки при равноточных измерениях
	Пример 1.1.
2.	Метод наименьших квадратов (МНК)
	Пример 2.1.
3.	Численное интегрирование
	Пример 3.1.
4.	Задания контрольной работы
	Задача 1
	Задача 2
	Задача 3
5.	Таблицы
6.	Контрольные вопросы
7.	Литература

ВВЕДЕНИЕ

Методические указания по курсу «Вычислительная математика и статистическая обработка данных» содержат решение тестовых примеров с предыдущим им необходимым теоретическим материалом, варианты контрольной работы, таблицы, используемые в статистической обработке данных; контрольные вопросы, список литературы.

Оценки истинного значения измеряемой величины

Понятие о типах оценок и их свойствах

Пусть даны результаты n независимых измерений некоторой величины. Предполагается, что эти результаты х₁, х₂, …, х_n свободны от грубых и систематических ошибок. Как известно из математической статистики оценить истинное значение а измеряемой величины – это значит:

а) указать такую функцию 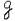(х₁, х₂, …, х_n) от результатов измерений, которая дает достаточно хорошее приближение к значению а. Такая функция называется точечной оценкой или просто оценкой значения а;

б) указать границы интервала ( 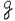q -δ; 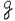q+δ), который с заданной вероятностью покрывает истинное значение а. Такая оценка называется доверительной оценкой, вероятность Р – доверительной вероятностью или надежностью оценки, интервал ( 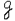q -δ; 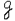q+δ) – доверительным интервалом, а его границы – доверительными границами.

Чтобы обеспечить достаточно хорошее приближение к истинному значению а , оценка 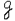q (х₁, х₂, …, х_n) должна (по возможности) быть несмещенной, состоятельной и эффективной.

Точечные оценки

Если все n измерений величины а произведены с одинаковой точностью (равноточные измерения), то в качестве истинного значения α измеряемой величины применяют среднее арифметическое значение результатов измерений:

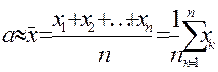(1)

Эта оценка является несмещенной и состоятельной. При дополнительном предположении, что случайные ошибки измерения подчинены нормальному закону распределения вероятностей, эта оценка является эффективной.

Если измерения не являются равноточными, но известны веса измерений, т.е. числа р₁, р₂, …, р_n обратно пропорциональные дисперсиям

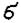
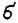
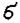
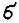
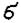
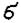ошибок ₁², ₂², …, _n²: р₁:р₂: …: р_n = 1/ ₁²:1/ ₂² : … :1/ _n², то в качестве оценки истинного значения а измеряемой величины применяют взвешенное среднее арифметическое значение

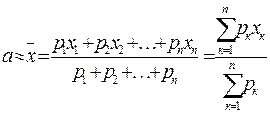(2)

Эта оценка обладает теми же свойствами, что и оценка (1).

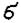Например, часто обрабатываемые результаты х₁, х₂, …, х_n представляют собой не результаты непосредственных измерений, а среднее в n сериях измерений, произведенных с одной и той же точностью (т.е. с одинаковой средней квадратической ошибкой ), но при разных количествах измерений в каждой серии. В этом случае каждому значению х_к можно приписать в качестве веса количество измерений в соответствующей серии:

р_к=m_к (к=1, 2, …, n)

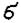где m_к – количество измерений в серии со средним значением х_к, обратно пропорциональны количествам измерений m_к в соответствующих сериях:

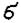
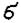
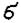
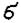
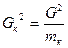и, значит, 1/ ₁²:1/ ₂² : … :1/ _n² = m₁: m₂: …: m_n

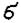Среднее арифметическое значение для интервального ряда данных является смещенной оценкой для а. Величина смещения имеет порядок h², если длина интервала h достаточно мала (в 2-3 раза меньше, чем ).

Доверительные оценки при равноточных измерениях

Доверительные оценки истинного значения α измеряемой величины будем рассматривать в предположении, что случайные ошибки измерения подчинены нормальному закону распределения вероятностей и только симметричные доверительные оценки, которые имеют вид неравенств

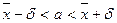
или 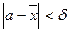(3)

где 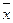- среднее арифметическое значение (1) или (2).

Величина δ определяется по заданной доверительной вероятности (надежности оценки) , обычно надежность задается в виде одного из трех уровней 0,95; 0,99 или 0,999.

а) Доверительная оценка при известной точности измерений.

Если заранее известна средняя квадратическая ошибка G (или другая связанная с ней характеристика точности измерений), то доверительная оценка (3) имеет вид

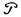
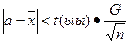(4)

где n – число измерений, а значение t=t(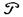) определяется по заданной доверительной вероятности 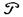из условия

2Φ(t)=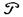 (5)

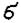т.е. находится по таблице II.

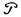Таким образом, здесь .

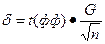б) Доверительная оценка при неизвестной точности измерений.

Если средняя квадратическая ошибка заранее неизвестно, то вместо нее используют эмпирический стандарт (исправленное среднее квадратическое отклонение)

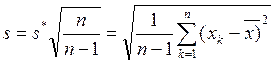(6)

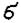(где s^* - среднее квадратическое отклонение) который служит оценкой параметра G.

При этом доверительная оценка (3) принимает вид

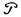
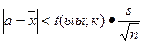(7)

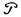
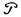или 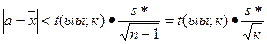, (к = n-1),

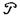
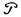где множитель t( ; к) зависит уже не только от доверительной вероятности, но и от числа измерений n (к = n-1). Значения этого множителя для различных значений k ≥4 приводятся в таблице IV, составленной с помощью так называемого распределения Стьюдента, т.е. распределения вероятностей отношения 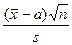: значения t=t(ss ;к) определяются так, что

..

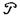
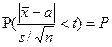Распределение Стьюдента зависит от одного параметра k, который называется числом степеней свободы; для рассматриваемой задачи число степеней свободы k связано с числом измерений n соотношением k=n-1.

Пример 1.1.

Даны результаты N=30 измерений:

хк		112,5		119,5		126,5		133,5
mк

где m_к – частота х_к

а) требуется оценить истинное значение измеряемой величины а с надежностью Р = 0,99, предполагая, что случайные ошибки измерения подчинены нормальному закону распределения вероятностей;

б) х_*=144 результат тридцать первого измерения исключен как «выскакивающее». С какой надежностью исключен из рассмотрения х_*?

Решение. а) Истинное значение измеряемой величины а равно математическому ожиданию случайной величины Х, принимающей конкретные значения х_к. Поэтому задача сводится к оценке математического ожидания (при неизвестном G ) при помощи доверительного интервала

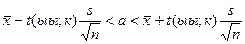
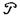покрывающего а с заданной надежностью Р =0,99.

Вычислим среднее арифметическое 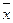и эмпирический стандарт s всех тридцати измерений. Вычисление этих величин значительно упрощается, если отсчет значений х_к вести от подходящим образом выбранного начала отсчета с и в подходящем масштабе. Практически это сводится к линейной замене

х_к= с +hu_к (к=1, 2, …, n).

При такой замене расчетные формулы принимают вид

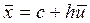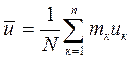
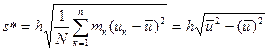, где

, где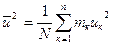

Для контроля вычислений весь расчет повторяют с другими началом отчета с₁: результаты должны совпасть с точностью до возможных ошибок округления. Для проведения вычислений составляем таблицу: первые два столбца исходные данные; выбирая за начало отсчета с=123 и полагая h=3,5 подсчитываем значения

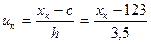
для третьего столбца. Сумма чисел четвертого и пятого столбцов дают все данные для расчета 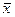и s*. В последних трех столбцах проведены контрольные расчеты при другом начале отсчета с₁=126,5, что соответствует сдвигу u_к=v_к+1

Исходные данные	Расчет	Контроль
хк	mк	uк	mк uк	mк uк2	vк	mк vк	mк vк2
		-4	-4		-5	-5
112,5		-3	-6		-4	-8
		-2	-6		-3	-9
119,5		-1	-5	-	-2	-10
					-1	-7
126,5
133,5
сумма		-			-	-29

С помощью полученных сумм подсчитываем средние:

, ,

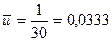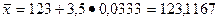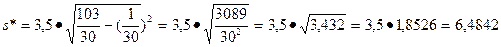
Контрольные расчеты дают те же результаты:

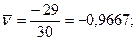
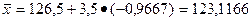
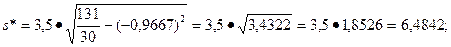
Используя формулу s=s* 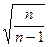находим:

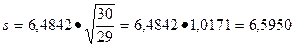
Далее по таблице IV находим t(0,99; 29)=2,758 и

,

,

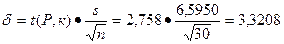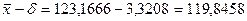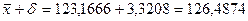
Ответ: Интервал (119,846; 126,487) покрывает истинное значение а измеряемой величины с надежностью 99%.

б) Вычислим отношение 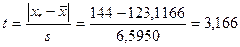и сравниваем с критическими значениями t_n( ) из таблицы III. При данном числе n=30 приемлемых результатов это отношение t=3,166 оказалось между t₃₀(0,99)=2,802 и t₃₀(0,999)=3,719, следовательно с надежностью вывода, большей =0,99, можно считать, что «выскакивающее» значение х_*=144 содержит грубую ошибку.

Ответ: х_*=144 исключен из дальнейшего рассмотрения с надежностью более 99%.