Предельные вероятности состояний

Пусть имеется система S c дискретными состояниями, в которой протекает марковский процесс с непрерывным временем.

Что будет с системой S при t ® ¥ ? Будут ли функции p₁(t), p₂(t), ..., p_n(t) стремиться к каким-то пределам? Эти пределы, если они существуют, называются предельными (или "финальными") вероятностями состояний.

Можно доказать следующее общее положение:

Если число состояний системы S конечно и из каждого состояния можно перейти (за то или иное число шагов) в каждое другое, то предельные вероятности состояний существуют и не зависят от начального состояния системы.

Предположим, что поставленное условие выполнено, и предельные вероятности существуют:

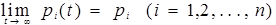
Очевидно, предельные вероятности состояний, также, как и допредельные, в сумме должны давать единицу:

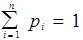
Таким образом, при t®¥ в системе S устанавливается некоторый предельный стационарный режим: он состоит в том, что система случайным образом меняет свои состояния, но вероятность каждого из них уже не зависит от времени. Каков смысл вероятности? Она представляет собой среднее относительное время пребывания системы в данном состоянии.

Как вычислить предельные вероятности? В системе уравнений Колмогорова надо положить все производные равными нулю.

Пример 1. Вычислить предельные вероятности для системы:

Пример 2. Написать уравнения для предельных вероятностей.

Пример 3. Найти предельные вероятности для системы.

9. Процесс "гибели и размножения".

Марковский поцесс называется "процессом гибели и размножения", если его граф состояний вытянут в цепочку, т.е. только l_n,n+1 и . l_n,n-1 не равны нулю, т.е. не равны нулю только плотности вероятностей перехода в соседнее состояние.

Пример 1. Техническое устройство состоит из трех одинаковых узлов; каждый из них может выходить из строя (отказывать); отказавшее устройство немедленно начинает восстанавливаться. Состояние системы нумеруем по числу неисправных узлов.

В дальнейшем для процесса гибели и размножения будем обозначать l_n,n+1=l_n, l_n,n-1=m_n.

Определим общую схему решения для процессов гибели и размножения. Напишем алгебраические уравнения для вероятностей состояний

Для первого состояния S₁ имеем:

l₁p₁=m₂p₂

(9.1)

Для второго состояния имеем:

l₂p₂+m₂p₂=l₁p₁+m₃p₃

(9.2)

Но в силу (9.1) можно сократить справа и слева равные друг другу члены l₁p₁ и m₂p₂, получим

l₂p₂=m₃p₃

и далее, совершенно анологично,

l₃p₃=m₄p₄

и вообще для всех k

l_kp_k=m_k+1p_k+1 для k=1,2,..., n-1

Решение этой системы есть:

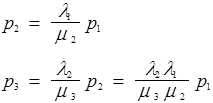
и вообще

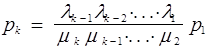
В силу

p₁+p₂+....+p_n = 1

имеем

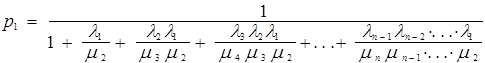
(9.8)

а

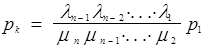
(9.9)

Пример 2. Найти предельные вероятности состояний для процесса гибели и размножения с графом

Пример 3. Прибор состоит из трех узлов; поток отказов - простейший, среднее время безотказной работы каждого узла равно Т_в. Отказавший узел сразу же начинает ремонтироваться; среднее время ремонта (восстановления) узла равно t_p; закон распределения этого вемени показательный (поток восстановлений - простейший). Найти среднюю производительность прибора, если при трех работающих узлах она равна 100%, при двух - 50%, а при одном и менее - прибор вообще не работает.