Серединний трикутник і пряма Ейлера
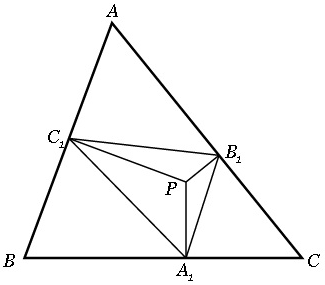
Трикутник, отриманий з’єднанням середин сторін даного трикутника, називається серединним трикутником. На малюнку 13 трикутник А′В′С′ є серединним трикутником трикутника АВС. Розглянемо також дві медіани АА′ і ВВ′, які перетинаються в точці G, дві висоти трикутника АВС, які перетинаються в точці Н, і дві висоти трикутника А′В′С′, перетинаються в точці О. Сторони трикутника А′В′С′ паралельні сторонам трикутника АВС, тому ці трикутники подібні. 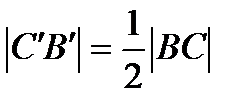 , тому відношення довжин будь-яких двох відповідних відрізків (а не тільки відповідних сторін) буде дорівнювати 1 : 2. В дійсності відрізки В′С′, С′А′, А′В′ розбивають трикутник АВС на чотири конгруентних трикутники. До речі, точка Р - середина відрізка В′С′ - також є і серединою відрізка АА′.
, тому відношення довжин будь-яких двох відповідних відрізків (а не тільки відповідних сторін) буде дорівнювати 1 : 2. В дійсності відрізки В′С′, С′А′, А′В′ розбивають трикутник АВС на чотири конгруентних трикутники. До речі, точка Р - середина відрізка В′С′ - також є і серединою відрізка АА′.
Далі можна бачити, що АС′А′В′ - паралелограм, звідси, пряма АА′ ділить навпіл відрізок В′С′. Томму медіани трикутника А′В′С′ лежать на медіанах трикутника АВС, а це означає, що обидва трикутники мають один і той самий центроїд G.
Висоти трикутника А′В′С′, зображені на малюнку, є серединними перпендикулярами сторін АВ і ВС трикутника АВС. Звідси можна зробити висновок, що точка О – ортоцентр трикутника А′В′С′ - є в той же час і центром кола, описаного навколо трикутника АВС.
Так як точка Н – ортоцентр трикутника АВС, а точка О – ортоцентр подібного йому трикутника А′В′С′, то 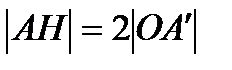 .
.
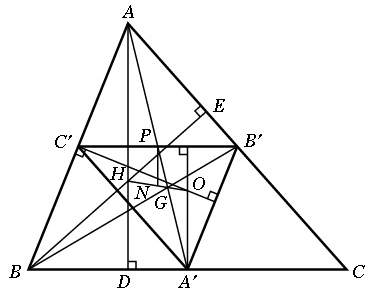
Мал. 13.
Згадаємо, що за теоремою 3.2(ст. 9). 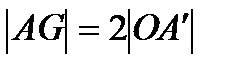 . І, нарешті, так як обидва відрізка, AD і OA′, перпендикулярні стороні ВС, то вони паралельні. Звідси,
. І, нарешті, так як обидва відрізка, AD і OA′, перпендикулярні стороні ВС, то вони паралельні. Звідси,
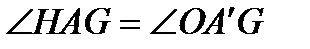 ,
, 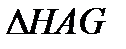 ∽
∽ 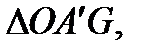
.
Звідси, точки O, G, H колінеарні ( лежать на одній прямій) і 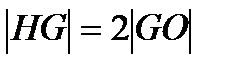 , тобто виконується наступна теорема.
, тобто виконується наступна теорема.
Теорема 7.1. Ортоцентр, центроїд і центр описаного кола довільного трикутника лежать на одній прямій. Центроїд ділить відстань від ортоцентру до центру вписаного кола в відношенні 2 : 1.
Пряма, на якій лежать ці три точки, називається прямою Ейлера цього трикутника.
Розглянемо малюнок 13 більш детально. Ми відзначили точку N, де пряма Ейлера НО перетинає пряму, яка проходить через точку Р перпендикулярно В′С′. Всі три прямі АН, PN i A′O, перпендикулярні до відрізка В′С′, паралельні. Так як 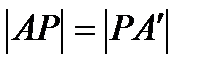 , то пряма PN рівновіддалена від прямих АН і А′О. Відповідно, точка N – середина відрізка НО.
, то пряма PN рівновіддалена від прямих АН і А′О. Відповідно, точка N – середина відрізка НО.
До сих пір в міркуваннях фігурувала сторона В′С′ трикутника А′В′С′. Якщо проводити ті ж міркування, але стосовно до якої-небудь іншої сторони цього трикутника, то відрізок НО залишиться тим же, і він буде ділитись пополам серединним перпендикуляром до нової сторони. Так як у відрізка НО тільки одна середина, то можна стверджувати, що серединні перпендикуляри всіх трьох сторін трикутника А′В′С′ будуть проходити через точку N. Іншими словами, точка N повинна бути центром кола, описаного навколо трикутника А′В′С′.
Отже, центр кола, описаного навколо серединного трикутника, лежить на середині відрізка НО прямої Ейлера вихідного трикутника. Крім того, так як трикутник А′В′С′ подібний трикутнику АВС, то радіус кола, описаного навколо серединного трикутника, дорівнює половині радіуса кола, описаного навколо вихідного трикутника.
Задача 9.
Показати, що 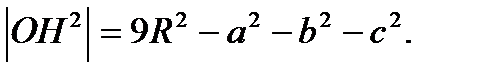 (мал.. 13).
(мал.. 13).
Перш ніж довести дану рівність я доведу таке твердження:
Твердження 1: нехай АХ – чевіана довжини р і 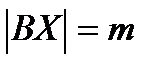 ,
, 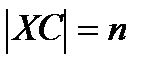 (мал. 13.1). Тоді
(мал. 13.1). Тоді
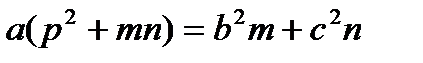
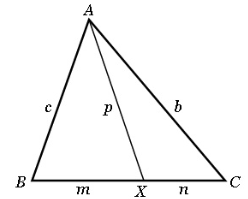
Мал. 13.1.
Доведення твердження.
Розглянемо трикутник АВС.
За теоремою косинусів: 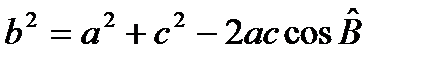
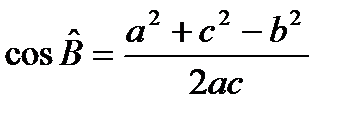 .
.
Розглянемо трикутник ABX.
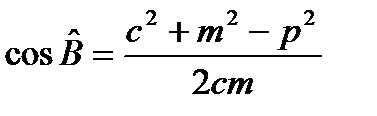 .
.
Отже:
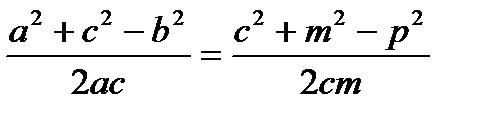 .
.
Домноживши ліву і праву частини на 2с і використавши властивість пропорції отримаємо:
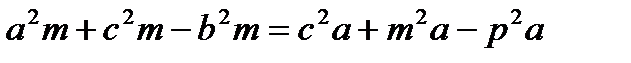 ,
,
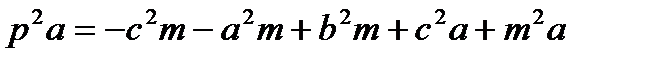 ,
,
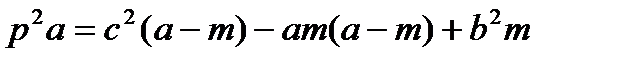 ,
,
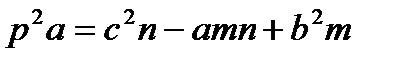 ,
,
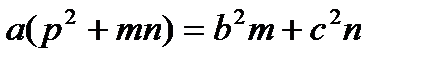 .
.
Твердження доведене.
Доведення задачі.
З малюнку 12(ст. 17) можна побачити, що
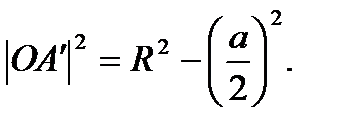
Позначивши 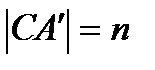 , маємо
, маємо 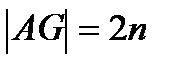 і
і 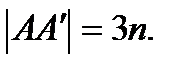 Тому маємо:
Тому маємо:
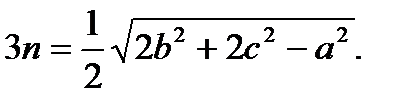
Далі можна застосувати твердження 1 до трикутника ОАА′. Отримаємо:
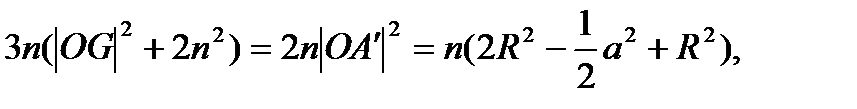
Звідси
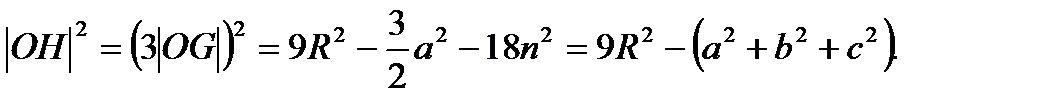
Коло дев’яти точок.
Розглянемо новий малюнок, на якому К, L, М – середини відрізків АН, ВН, СН, які лежать на висотах. Так як ВС – спільна сторона двох трикутників АВС і НВС, а точки С′, В′ і L, M є серединами інших їх сторін відповідно, то відрізки С′В′ і LM паралельні прямій ВС (а їх довжини рівні половині довжини відрізка ВС). Аналогічно, так як АН – спільна сторона двох трикутників ВАН і САН, то обидва відрізка С′L і В′М паралельні прямій АН (а їх довжини рівні половині довжини відрізка АН).
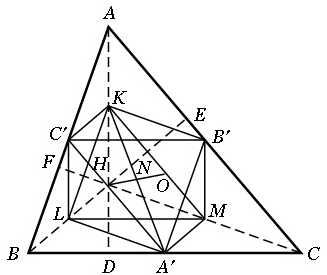
Мал. 14.
Звідси, B′C′LM – паралелограм. Так як відрізки ВС і АН– перпендикулярні, то цей паралелограм – прямокутник. Аналогічно, A′B′KL – прямокутник (як і С′А′МК). Звідси, А′К, В′L, С′М є трьома діаметрами кола, як показано на малюнку 15.
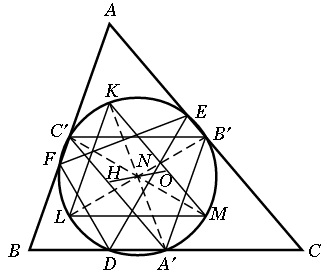
Мал. 15.
Так як кут А′DK – прямий, це коло (побудоване на відрізку А′К, як на діаметрі) проходить через точку D. Так само вона проходить через точки Е і F. Сумуючи вищесказане, отримуємо:
Теорема 8.1. Основи трьох висот довільного трикутника, середини трьох його сторін і середини трьох відрізків, які з’єднують його вершини з ортоцентром, лежать всі на одному колі радіуса 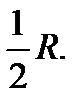
Будемо називати його колом дев’яти точок цього трикутника. Так як три точки К, L, М діаметрально протилежні точкам А′, В′, С′, то кожен із двох трикутників КLМ або А′ В′ С′ можна отримати з іншого поворотом на 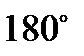 навколо центру цього кола. Очевидно, що цей поворот, який міняє місцями ці два конгруентних трикутники, також повинен поміняти місцями і їх ортоцентри Н і О. Звідси, центром кола дев’яти точок є середина відрізка НО, яку уже раніше я позначав через N, маючи на увазі її майбутню роль центра кола дев’яти точок. Іншими словами:
навколо центру цього кола. Очевидно, що цей поворот, який міняє місцями ці два конгруентних трикутники, також повинен поміняти місцями і їх ортоцентри Н і О. Звідси, центром кола дев’яти точок є середина відрізка НО, яку уже раніше я позначав через N, маючи на увазі її майбутню роль центра кола дев’яти точок. Іншими словами:
Теорема 8.2. Центр кола дев’яти точок лежить на прямій Ейлера, точно посередині відрізка між ортоцентром і центром описаного кола.
Задача 10.
Нехай три конгруентні кола мають спільну точку і перетинаються ще в трьох точках А, В і С. Тоді радіус кожного із кіл рівний радіусу кола описаного навколо трикутника АВС, а їх спільна точка є ортоцентром цього трикутника.
Нехай Р – спільна точка, а 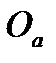 ,
, 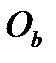 ,
, 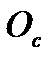 - центри трьох конгруентних кіл РВС, РСА, РАВ.
- центри трьох конгруентних кіл РВС, РСА, РАВ.
Тоді чотирикутники Р 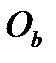 А
А 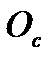 і Р
і Р 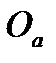 С
С 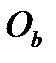 - ромби. Звідси,
- ромби. Звідси, 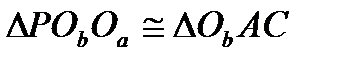 і
і 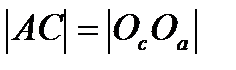 . Аналогічно
. Аналогічно 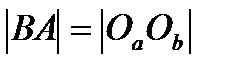 і
і 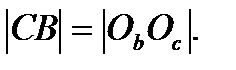 Звідси,
Звідси, 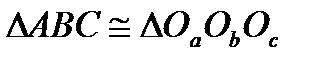 і, звичайно, конгруентні трикутники мають однакові радіуси описаних навколо них кіл. Так як відрізок АР перпендикулярний відрізку
і, звичайно, конгруентні трикутники мають однакові радіуси описаних навколо них кіл. Так як відрізок АР перпендикулярний відрізку 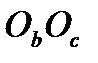 , який паралельний відрізку ВС, то висотами трикутника АВС є прямі АР, ВР, і СР. Тому точка Р співпадає з точкою Н.
, який паралельний відрізку ВС, то висотами трикутника АВС є прямі АР, ВР, і СР. Тому точка Р співпадає з точкою Н.
Педальний трикутник.
Ортотрикутник та серединний трикутник є двома прикладами додаткових трикутників більш загального типу. Нехай Р – будь-яка точка всередині даного трикутника АВС, і нехай перпендикуляри, опущені з точки Р на сторони ВС, СА, АВ трикутника будуть 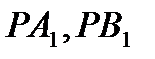 і
і 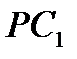 , як на малюнку 16. Трикутник
, як на малюнку 16. Трикутник 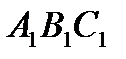 , вершинами якого є основи цих перпендикулярів, називається педальним трикутником трикутника АВС для “педальної точки” Р.
, вершинами якого є основи цих перпендикулярів, називається педальним трикутником трикутника АВС для “педальної точки” Р.
Мал. 16.
Необхідність в тому, щоб точка Р знаходилась всередині трикутника, можна послабити, заперечивши лиш точці Р знаходитися на колі, описаному навколо трикутника АВС. Ясно, що якщо точка Р – ортоцентр, то виникає ортотрикутник, а якщо вона – центр вписаного кола, то виникає серединний трикутник.
Розглянемо малюнок 16 більш детально. Прямі кути в точках 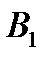 і
і 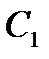 вказують на те, що ці точки лежать на колі з діаметром АР, іншими словами, точка Р лежить на колі, описаному навколо трикутника
вказують на те, що ці точки лежать на колі з діаметром АР, іншими словами, точка Р лежить на колі, описаному навколо трикутника 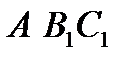 . Застосувавши теорему синусів до цього трикутника, а також до самого трикутника АВС, отримаємо
. Застосувавши теорему синусів до цього трикутника, а також до самого трикутника АВС, отримаємо
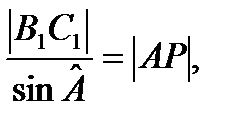
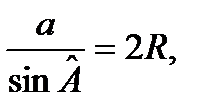
звідси
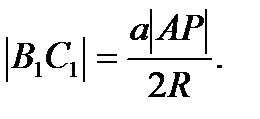
Аналогічно,
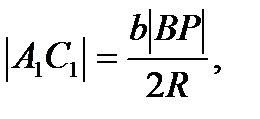 і
і 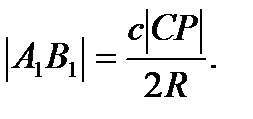
Таким чином, доведена наступна теорема
Теорема 9.1. якщо відстані від педальної точки до вершин трикутника АВС рівні x, y, z, то довжини сторін педального трикутника дорівнюють
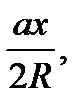
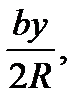
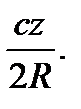
Перейдемо до дуже цікавої задачі, в якій розглядаються педальні трикутники педальних трикутників. Вона, в свою чергу, чудово демонструє роль уяви в геометрії. Ця задача вперше появилась в 1892 році, коли вона була добавлена редактором Ж. Нойбергом в шосте видання класичної праці Джона Кейсі “Продовження перших шести книг Начал Евкліда”. На малюнку 17 внутрішня точка Р використана для визначення трикутника 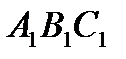 (першого) педального трикутника трикутника АВС. ТА ж сама педальна точка Р знову використана для визначення педального трикутника трикутника
(першого) педального трикутника трикутника АВС. ТА ж сама педальна точка Р знову використана для визначення педального трикутника трикутника 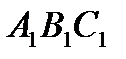 , який позначено через
, який позначено через 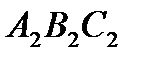 , назвемо його “другим педальним трикутником” трикутника АВС. Третя операція дає трикутник
, назвемо його “другим педальним трикутником” трикутника АВС. Третя операція дає трикутник 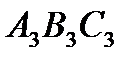 - педальний трикутник трикутника
- педальний трикутник трикутника 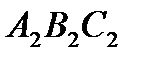 . Для “третього педального трикутника” використовувалась та сама точка Р.
. Для “третього педального трикутника” використовувалась та сама точка Р.
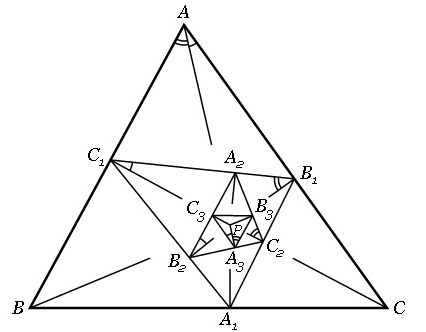
Мал. 17.
В цих термінах відкриття Нойберга можна виразити наступним чином:
Теорема 9.2. Третій педальний трикутник подібний до даного.
Доведення. Доведення є напрочуд простим. Воно слідує з малюнку, потрібно тільки з’єднати точки Р і А. Якщо розглянути кола описані навколо трикутників 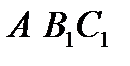 ,
, 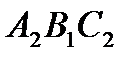 ,
, 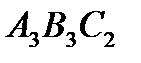 ,
, 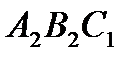 і
і 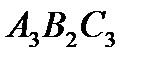 , то точка Р належить кожному із них, тому
, то точка Р належить кожному із них, тому
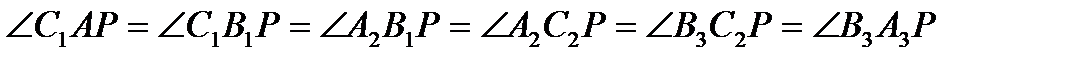
і
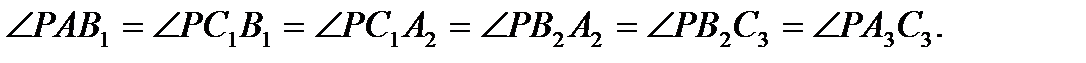
Іншими словами, дві частини на які пряма АР ділить кут А (позначені на малюнку одинарною і подвійною дугами), мають двійників: одна – при вершині 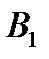 , а інша – при вершині
, а інша – при вершині 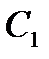 , дальше – при вершинах
, дальше – при вершинах 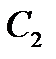 і
і 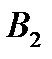 і, нарешті, обидві – при вершині
і, нарешті, обидві – при вершині 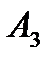 . Звідси, трикутник АВС і трикутник
. Звідси, трикутник АВС і трикутник 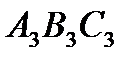 мають рівні кути при вершинах А і
мають рівні кути при вершинах А і 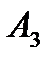 . Аналогічно, вони мають рівні кути при вершинах В і
. Аналогічно, вони мають рівні кути при вершинах В і 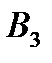 . Таким чином, теорема доведена.
. Таким чином, теорема доведена.
Цікаво прослідкувати “чергу кутів” з положення А в положення 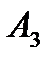 - настільки ж чіткий, як і маневри добре підготовленої команди.
- настільки ж чіткий, як і маневри добре підготовленої команди.
Ця властивість продовження педальних трикутників була узагальнена доктором А. Опенгеймом, проректором Малазійського університету в Сінгапурі. Він встановив, що n-й педальний n-кутник будь-якого n-кутника подібний даному n-кутнику. Дуже повчально провести подібну побудову для четвертого педального чотирикутника, прослідкувавши ще більш довшу “чергу кутів”.
Задача 11.
Якщо всередині квадрата АВСD побудований рівнобедрений трикутник РАВ з кутами по 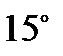 при основі АВ, як на малюнку 9.1, то точки Р, С, D є вершинами рівностороннього трикутника.
при основі АВ, як на малюнку 9.1, то точки Р, С, D є вершинами рівностороннього трикутника.
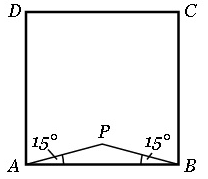
Мал. 9.1
Доведення проведемо методом від супротивного. Припустимо, що 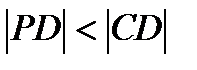 , тоді
, тоді 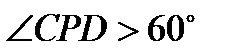 ,
, 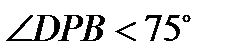 ,
, 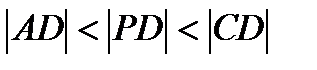 . Якщо, з іншої сторони,
. Якщо, з іншої сторони, 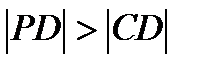 , то всі нерівності змінюються на протилежні. В будь-якому випадку чотирикутник не був би квадратом. Відповідно, якщо чотирикутник АВСD – квадрат, то обов’язково має виконуватися рівність
, то всі нерівності змінюються на протилежні. В будь-якому випадку чотирикутник не був би квадратом. Відповідно, якщо чотирикутник АВСD – квадрат, то обов’язково має виконуватися рівність 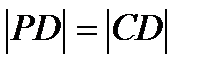 . Отже РСD – рівносторонній трикутник.
. Отже РСD – рівносторонній трикутник.
Висновок.
У цій дипломній роботі я почав з добре відомих понять. Виявив ряд простих, але дуже важливих фактів. Дана тема є актуальною, оскільки Евклідова геометрія – це перша аксіоматична теорія в математиці. Як бачимо, з трикутником пов’язано ряд цікавих і дуже важливих елементів теорії, які можна використати для доведення багатьох теорем. Методи, описані в цій роботі, можна використовувати для розв’язку багатьох задач, зв’язаних власне з трикутником, вписаним і описаним колом, чевіанами і так далі.
Після кожного розділу мною були підібрані та розв’язані задачі, які можна використати для проведення різних математичних олімпіад.
