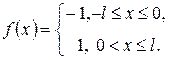Визначений інтеграл. Формула Ньютона-Лейбніца. Невласні інтеграли. Ряд Фур’є

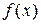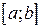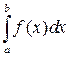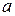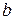Якщо функція неперервна на , тоді вона інтегровна на ньому, тобто існує визначений інтеграл: , де числа і називаються нижньою і верхньою межею інтегрування функції 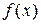відповідно. Відзначимо деякі основні властивості визначеного інтеграла, а саме:

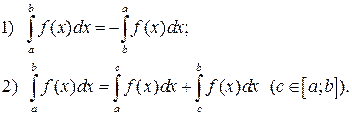(29)

Щоб обчислити визначений інтеграл, скористаємось основною формулою інтегрального числення (формула Ньютона-Лейбніца)

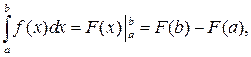(30)

де 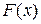– первісна функції .

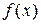Приклад 1.Обчислити інтеграл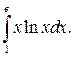

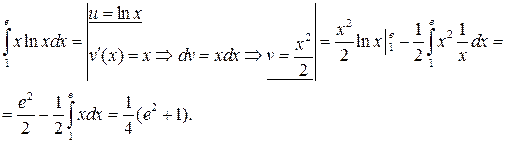
Приклад 2.Обчислити інтеграл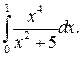

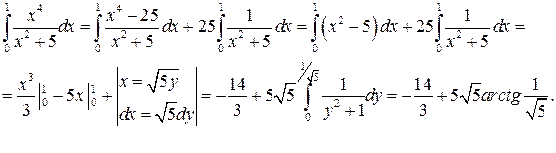
Зробивши заміну в підінтегральному виразі, ми одразу змінили межі інтегрування: коли і при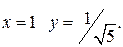

Приклад 3.Обчислити площу фігури, яка обмежена графіками функцій 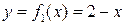і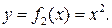

Якщо фігура обмежена графіками неперервних функцій 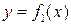і 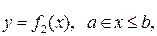то її площа може бути обрахована за формулою:

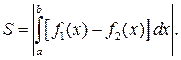(31)

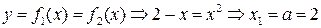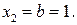Знайдемо спочатку абсциси точок перетину цих функцій, які і будуть межами інтегрування: і За формулою (31) маємо:

.

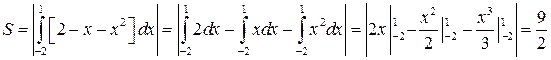Приклад 4.Визначити роботу, необхідну для запуску супутника масою т з поверхні Землі вертикально вверх на висоту .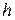

Робота змінної сили 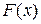по переміщенню тіла з початкової точки 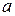в кінцеву точку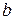 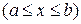визначається за формулою:

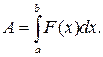(32)

Згідно із законом Ньютона, сила притягання супутника Землею визначається за формулою 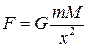, де 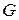– гравітаційна стала, М – маса Землі, х – відстань від супутника до центра Землі: 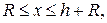де 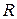– радіус Землі. За формулою (32) маємо:

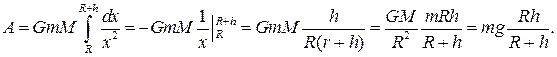
Тут ми врахували той факт, що при 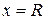сила притягання супутника Землею дорівнює його вазі, тобто: 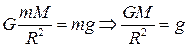(прискорення вільного падіння біля поверхні Землі).

Нехай функція 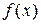визначена, наприклад, на проміжку 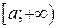та інтегровна на будь-якому відрізку 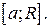Тоді скінчену границю

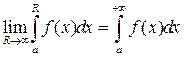(33)

називають невласним інтегралом першого роду.

Приклад 5.Обчислити інтеграл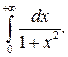

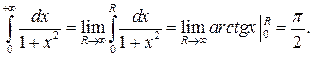
Приклад 6.Обрахувати роботу, необхідну для виведення супутника в міжпланетний простір. Це означає, що 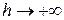(див. приклад 4). Отже,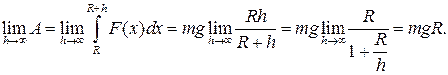

Нехай функція 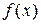визначена, наприклад, на проміж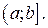ку Точку 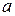будемо називати особливою, якщо функція 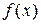не обмежена в будь-якому її околі, але обмежена та інтегровна на відрізку 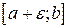. Тоді скінчену границю

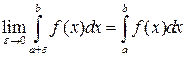(34)

називають невласним інтегралом другого роду.

Приклад 7. Обчислити інтеграл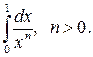

Точка 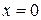є особливою для підінтегральної функції. Згідно з формулою (34) маємо:

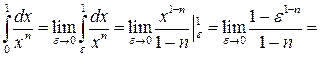
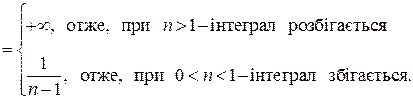
Окремо дослідимо поведінку інтеграла при :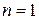

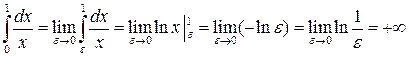
(інтеграл розбігається).

Нехай функція 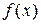визначена та інтегровна на 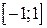. Тоді числа

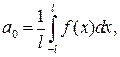(35)

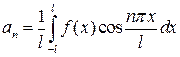при 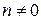(п – цілі числа), (36)

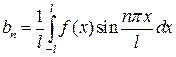(37)

називають коефіцієнтами Фур’є, а ряд

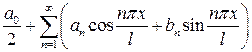(38)

називається рядом Фур’є функції .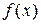

Якщо функція 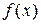парна, тоді при її інтегруванні за симетричними межами справедлива формула:

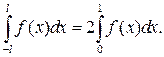(39)

Якщо функція 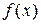непарна, тоді інтеграл від неї за симетричними межами тотожно дорівнює нулю.

Зауваження.Якщо функція 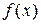парна, тоді коефіцієнти 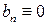, а якщо непарна, тоді коефіцієнти .

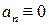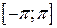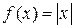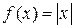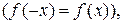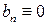Приклад 8.Розкласти в ряд Фур’є на функцію . Оскільки функція є парною тоді і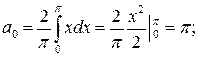

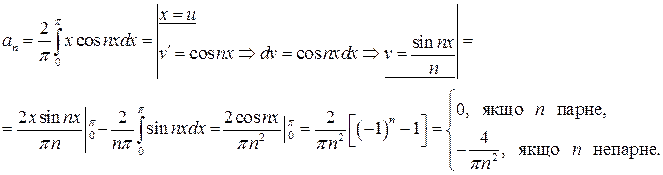
Отже, шуканий ряд Фур’є функції має такий вигляд:

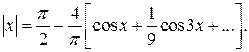
Завдання для самостійної роботи

1. Доведіть, що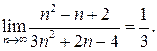

2. Доведіть, що: 1)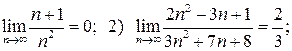

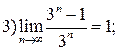
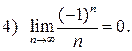
3. Доведіть, що послідовність 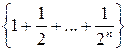має границю, рівну 2.

4. Доведіть, що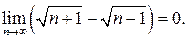

У задачах 5 – 18 знайдіть границі:

5. 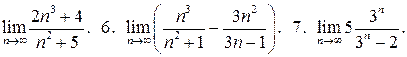8.

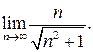
9.

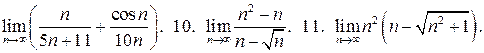
12.

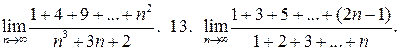
14.

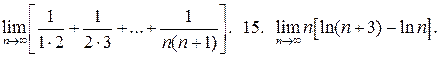
16.

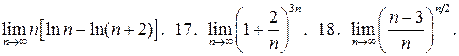
Шляхом порівняння з гармонічним рядом або зі спадною геометричною прогресією дослідіть збіжність рядів:

19.

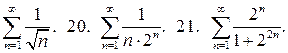
За допомогою ознаки Даламбера дослідіть на збіжність рядів:

22.

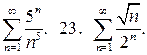
Дослідіть збіжність рядів:

24.

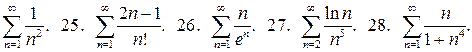
Дослідіть на абсолютну та умовну збіжність такі ряди:

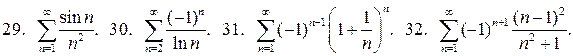
33.

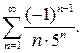
Знайти радіус та інтервал збіжності ряду і дослідити його збіжність на межах інтервалу:

34.

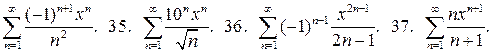
У задачах 38 – 42 знайдіть область визначення функцій, які задані формулами:

38.

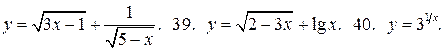
41.

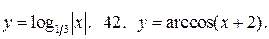
Знайдіть границі:

43. 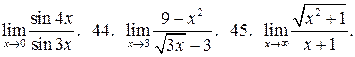46.

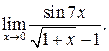
47.

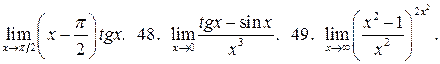
50.

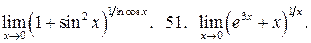
У задачах 52 – 54 знайдіть, яка з функцій є парною, непарною і яка не є ні парною, ні непарною:

52.

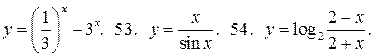
У задачах 55 – 56 знайдіть період функцій:

55.

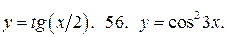
У задачах 57 – 68 знайдіть похідні функцій:

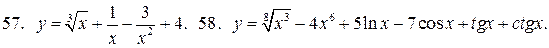
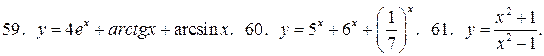
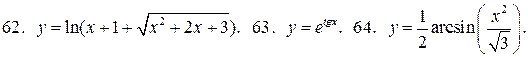
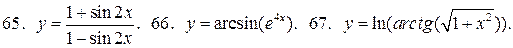
68.

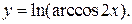
69. Складіть рівняння дотичної до графіків функцій:

1) 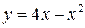– у точках перетину з віссю Ох;

2) 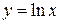– у точці перетину з віссю Ох;

3) 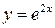– у точці перетину з віссю Оу.

70. Коло задано рівнянням 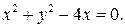Знайдіть рівняння дотичних до кола в точках його перетину з віссю Ох.

У задачах 71 – 75 знайдіть диференціали функцій:

71. 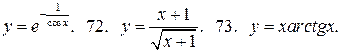74.

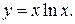
75.

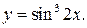
У задачах 76 – 78 знайдіть похідну другого порядку від функцій:

76.

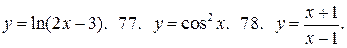
У задачах 79 – 81 знайдіть похідну третього порядку від функцій:

79.

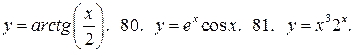
У задачах 82 –90 знайдіть границі за правилом Лопіталя:

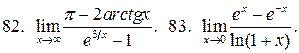
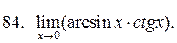
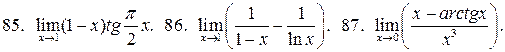
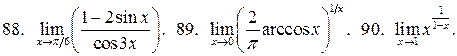
91. Розкладіть многочлен 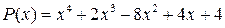за степенями 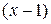за формулою Тейлора.

92. Розкладіть функцію 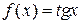за формулою Маклорена до члену з 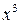включно.

93. Розкладіть функції за формулою Маклорена:

1) 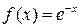до члена з 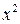включно; 2) 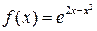до члена з ;

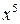3) 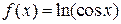до члена з 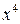; 4) 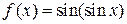до члена з .

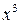У задачах 94 – 99 розкладіть функції в ряд Маклорена і знайдіть їх інтервали збіжності:

94. 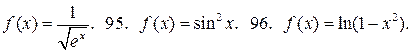97.

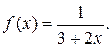
98.

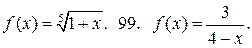
У задачах 100 – 104, використавши розклад Маклорена для відповідних функцій, знайдіть границі:

100. 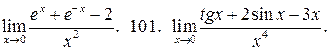102.

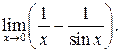
103.

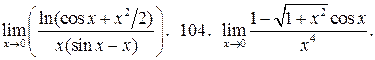
105. Знайдіть максимуми та мінімуми функцій:

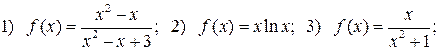
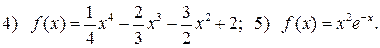
106. Знайти точки перегину графіка функцій:

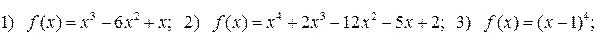
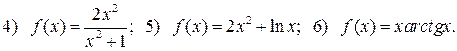
107. Знайдіть асимптоти графіків функцій:

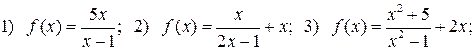
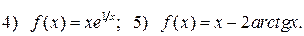
У задачах 108 – 115 побудуйте графіки функцій:

108.

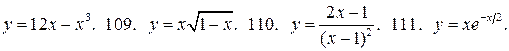
112.

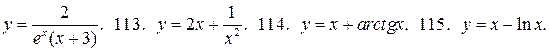
У задачах 116 – 121 знайдіть частинні похідні від функцій:

116.

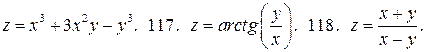
119.

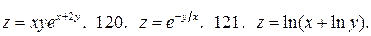
122. Для функції 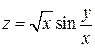доведіть, що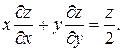

123. Знайдіть похідну за напрямком функції 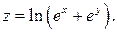Розгляньте напрямок, паралельний бісектрисі першого координатного кута.

124. Знайдіть похідну функції 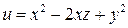у точці 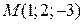за напрямком вектора 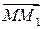, де 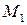– точка з координатами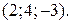

У задачах 125 – 128 знайти :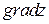

125. 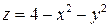у точці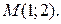

126. 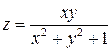у точці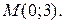

127. 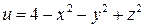у точці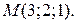

128. 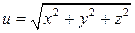у точці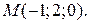

У задачах 129 – 132 знайдіть частинні похідні другого порядку:

129.

.

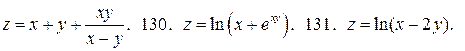
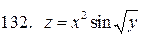133. Для функції 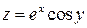доведіть, що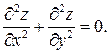

У задачах 134 – 137 знайдіть екстремуми функцій:

134.

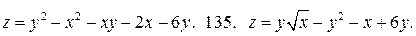
136.

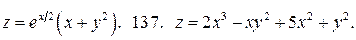
138. Нехай у результаті експерименту отримано п’ять значень шуканої функції у при п’яти значеннях її аргументу х:

х	-2
у	0.5		1.5

Знайдіть функціональну залежність між х та у у вигляді лінійної функції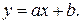

У задачах 139 – 141, безпосередньо інтегруючи, знайдіть інтеграли:

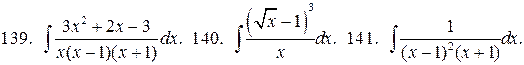
У задачах 142 – 155 за методом підстановки знайдіть інтеграли:

142. 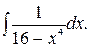143. 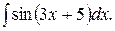144.

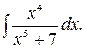
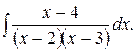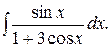
145. 146. 147.

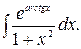
148. 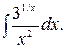149. 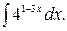150.

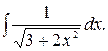
151. 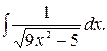152. 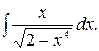153.

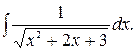
154. 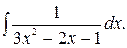155.

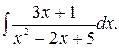
У задачах 156 – 161 за допомогою методу інтегрування частинами знайдіть інтеграли:

156. 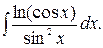157.

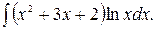
158. 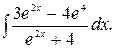159. 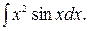160.

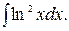
161.

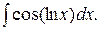
У задачах 162 – 193 обчисліть інтеграли:

162. 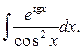163. 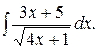164.

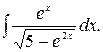
165. 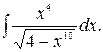166. 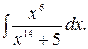167.

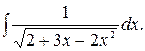
168. 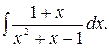169. 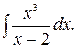170.

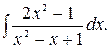
171. 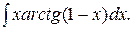172. 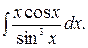173.

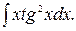
174. 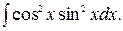175. 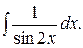176.

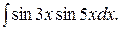
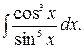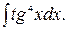177. 178. 179.

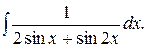
180. 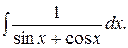181.

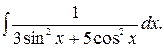
182. 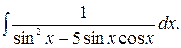183.

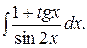
184. 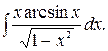185. 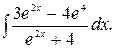186.

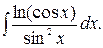
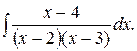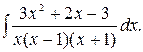187. 188. 189.

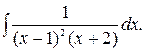
190. 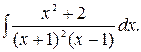191. 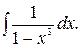192.

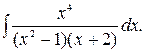
193.

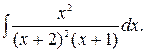
У задачах 194 – 201 обчисліть визначені інтеграли:

194. 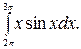195. 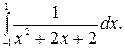196.

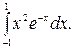
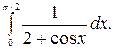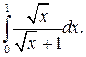197. 198. 199.

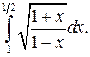
200. 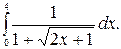201.

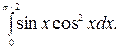
У задачах 202 – 206 знайдіть площу фігур, обмежених лініями:

202. 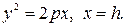203.

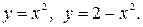
204.

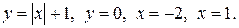
205. 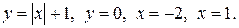206.

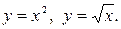
У задачах 207 – 217 дослідіть збіжність інтегралів:

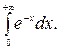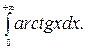207. 208. 209.

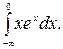
210. 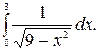211. 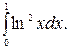212.

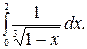
213. 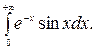214. 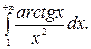215.

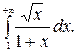
216. 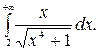217.

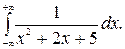
У задачах 218 – 220 розкладіть функції в ряд Фур’є на відрізку :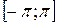

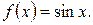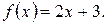218. 219. 220.

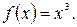
У задачах 221 – 222 розкладіть функції в ряд Фур’є на відрізку :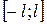

221. 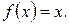222.