Определение закона распределения случайной погрешности

Задача определения закона распределения случайной погрешности решается в два этапа:

1) построение гистограммы или кумулятивной кривой распределения случайной погрешности и высказывание гипотезы о виде распределения;

2) Проверка гипотезы о виде распределения с помощью критерия согласия.

Гистограмма и кумулятивная кривая являются дискретными аналогами дифференциальной и интегральной функций распределения, построенными по статистической совокупности из п результатов наблюдений. Результаты наблюдений можно представить на числовой оси в виде точек 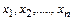. Разность между наибольшим и наименьшим наблюденным значением отсчетов равна диапазону результатов наблюдения

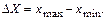
Этот диапазон можно разбить на L интервалов, длительностью

.

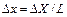Через границы этих интервалов можно записать формулу для интегральной функции распределения в следующем виде

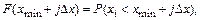
где

Если 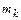- количество наблюденных значений, попавших в k-й интервал, то

.

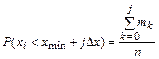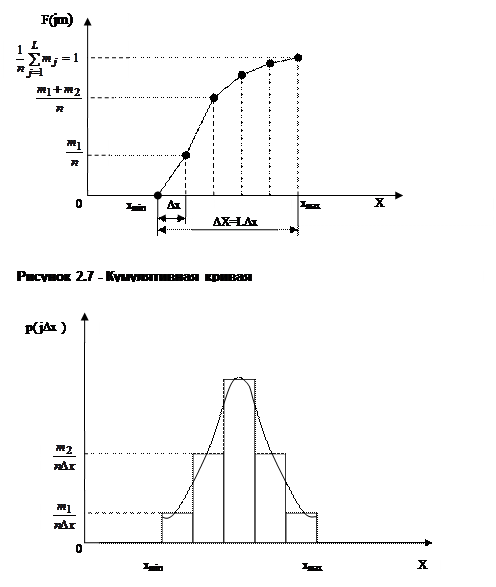
Эту зависимость можно представить в виде точек на графике 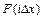(рис.2.7). Ломаная линия, соединяющая эти точки, называется кумулятивной кривой.

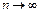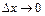В пределе, при и кумулятивная кривая стремится к интегральной функции распределения, сохраняя все ее свойства:

1) ;

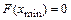2) ;

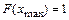3) 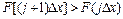- возрастающая функция.

Также, как интегральная функция распределения связана с дифференциальной кумулятивная кривая связана с гистограммой:

.

	Рисунок 2.8 - Гистограмма

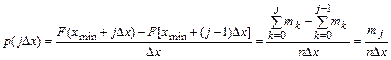Эта зависимость представлена на рис. 2.8 и представляет собой совокупность прямоугольников высотой 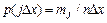. Гистограмма сохраняет все свойства дифференциального распределения, к которому стремится пр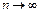и и :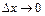

1) ;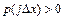

2) площадь под кривой гистограммы равна 1 (условие нормировки)

.

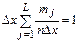При построении кумулятивных кривых и гистограмм для большей наглядности следует придерживаться следующих правил:

1) интервалы, на которые разбивается ось абсцисс, следует выбирать одинаковыми;

2) число интервалов L устанавливается в соответствии с рекомендациями, приведенными в табл.2.3;

Таблица 2.3 - К выбору числа интервалов гистограммы (кумулятивной кривой)

N	40-100	100-500	500-1000	1000-10000
L	7-9	8-12	10-16	12-22

3) масштаб гистограммы выбирается таким, чтобы высота гистограммы к ее основанию относились как 5:8.

После построения кумулятивной кривой и гистограммы можно высказать гипотезу о виде распределения.

Правдоподобие гипотез о соответствии распределения результатов наблюдения выбранному закону проверяют с помощью так называемых критериев согласия. Таких критериев существует множество. Рассмотрим некоторые из них, нашедшие наибольшее применение на практике.

Критерий Колмогорова.

В этом критерии в качестве меры расхождения теоретического и экспериментального распределения взято максимальное значение модуля разности D между экспериментальной F*(X) и теоретической F(X) интегральными функциями распределения

.

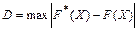Колмогоров доказал, что какова бы ни была функция распределения F(x) непрерывной случайной величины x, при неограниченном возрастании числа независимых наблюдений n, вероятность неравенства

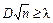
стремится к пределу

.

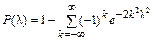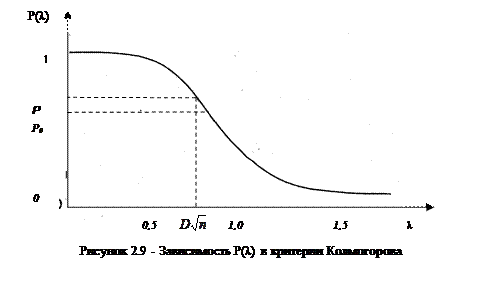
Зависимость 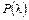изображена на рис.2.9 и в таблице А2.

Схема применения критерия Колмогорова заключается в следующем:

1) строится экспериментальная функция распределения F*(X) и предполагаемая F(X) теоретическая и определяется максимум D модуля разности между ними;

2) определяется величина ;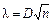

3) по таблице А2 находится вероятность 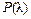того, что максимальное отклонение между F*(X) и F(X) не будет превышать D. Если 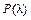мала, гипотезу отвергают.

Критерий Колмогорова очень прост и поэтому его охотно применяют на практике. Следует, однако, оговорить, что этот критерий можно применять только в случае, когда гипотетическое распределение F(X) полностью известно заранее из каких-либо теоретических соображений, т.е. когда известен не только вид функции F(X), но и входящие в нее параметры. Обычно на практике известен только общий вид функции F(X), а входящие в нее параметры определяются по данному статистическому материалу. В этом случае (при малом n) критерий Колмогорова дает завышенные значения вероятности 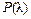, поэтому в иногда можно принять как правдоподобную гипотезу, в действительности плохо согласующуюся с опытными данными.

Критерий Пирсона (c²).

В качестве меры расхождения экспериментальных данных с теоретическим дифференциальным законом распределения вероятностей в критерии Пирсона принимается величина

,

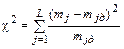где 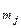- число результатов наблюдений, попавщих на j-й интервал гистограммы;

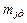- действительное число результатов наблюдений, которые попали бы на j-й интервал, при полном соответствии эмпирического закона распределения гипотетическому.

Значение 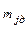рассчитывается по формуле

,

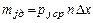где 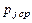- значение гипотетической функции распределения в точке, соответствующей средине j-го интервала гистограммы;

n – общее число наблюдений;

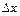- ширина интервала гистограммы.

Величина распределена по закону Пирсона (рис.2.10). Распределение зависит от параметра k, называемого числом “степеней свободы”.

Число степеней свободы равно числу интервалов гистограммы L минус число независимых условий, наложенных на эмпирическое распределение. Для симметричных законов распределения такими условиями являются:

1) условие нормировки ;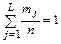

2) требование равенства математического ожидания гипотетического распределения среднему арифметическому экспериментального распределения ;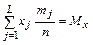

3) требование равенства дисперсии гипотетического распределения оценке дисперсии экспериментального распределения

.

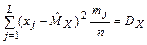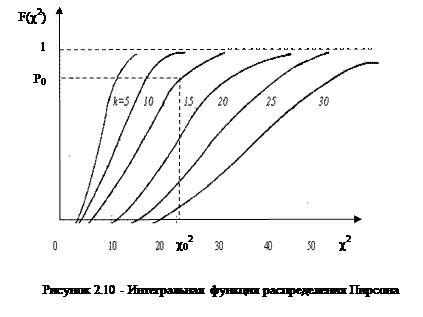
Поэтому k=L-3. Для распределения Пирсона составлены соответствующие таблицы (см. таблицу А3). Пользуясь этими таблицами можно найти для каждого c² и числа степеней свободы вероятность P₀ того, что величина, распределенная по закону c² превзойдет это значение.

На практике вероятностью Р₀ задаются и по таблицам определяют величину 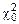. Если 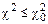, то гипотеза о виде закона распределения подтверждается, если 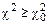, то отклоняется.

При проверке закона распределения по критерию Пирсона хорошие результаты получаются только если п > 40…50. Для n лежащем в диапазоне от 10…15 до 40...50 применяется так называемый составной критерий.