Раскрытие неопределенностей

Правило Бернулли-Лопиталя

I Понятие неопределенного выражения

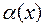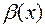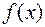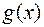Пусть и – бесконечно малые, а и – бесконечно большие функции при .

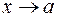Неопределенными выражениями (или неопределенностями) при 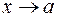называют следующие выражения:

1) 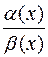– неопределенность вида ;

2) 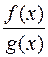– неопределенность вида ;

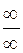3) 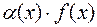– неопределенность вида ;

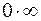4) 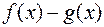– неопределенность вида ;

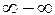5) 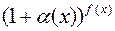– неопределенность вида ;

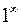6) 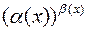– неопределенность вида ;

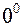7) 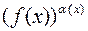– неопределенность вида .

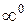Раскрыть неопределенность означает вычислить предел (соответствующего выражения) при .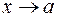

II Неопределенности вида , .

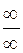Теорема Бернулли–Лопиталя. Пусть функци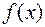и и 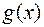удовлетво- ряют условиям: 1) определены и дифференцируемы на 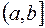; 2) 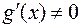; 3)выражение 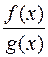являются при 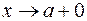неопределенностью вида или 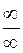. Тогда, если существует предел 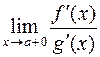(конечный или бесконечный), то существует и предел 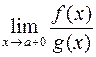, причем справедлива формула

.

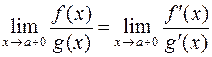Другими словами предел отношения двух б.м. или б.б. функций можно заменить пределом отношения их производных, если последний существует – это и есть правило Бернулли-Лопиталя.

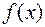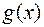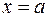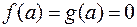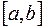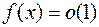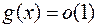Доказательство. Докажем теорему лишь для случая . Доопределим функции и в точке , положив их равными нулю: . Теперь эти функции непрерывны во всем замкнутом промежутке : их значение в точке а совпадают с пределами (ведь и при 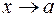), в других же точках непрерывность вытекает из дифференцируемости. К этой паре функций можем применить теорему Коши из §3:

,

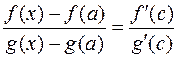где 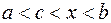. Учитывая, что функции в точке а равны нулю, получим

.

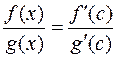Очевидно, что пр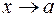и и 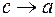. Правая часть последнего равенства имеет при 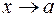предел 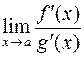(по условию теоремы), но тогда и левая часть имеет тот же самый предел.

Замечание 1. Аналогичное утверждение имеет место и для левого предела, а также для пределов на бесконечности, т.е. при .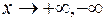

Пример 1. Для 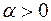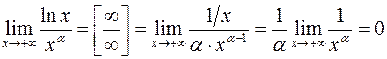. Этим пределом доказано, наконец, соотношение 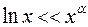, то есть 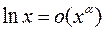при ( ).

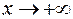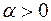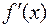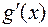Замечание 2. Если производные и удовлетворяют тем же требованиям, что и сами функци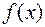и и 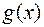, то правило Бернулли-Лопиталя можно применить повторно.

Пример 2. .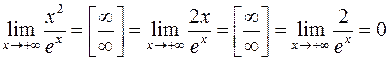

Нетрудно заметить, что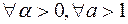

.

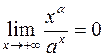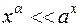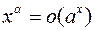Другими словами, или при .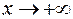

Замечание 3. Правило Бернулли-Лопиталя можно применять только, когда предел отношения производных существует. Например,

,

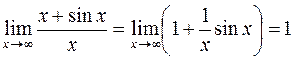но 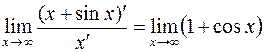не существует. Этот пример показывает, что из не-существования 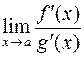нельзя делать вывод о .

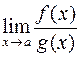Замечание 4. Существуют ситуации, в которых применение правила Бернулли-Лопиталя ничего не дает.

Пример 3. .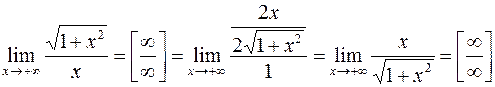

Еще одно применение правила вернет нас к исходному пределу.

III Другие виды неопределенностей.

Еще раз напомним, что правило Бернулли-Лопиталя применимо лишь к неопределенностям вида и 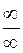. Все остальные неопределенности необходимо сводить к одной из этих двух путем алгебраических преобразований.

А) 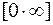. Так как 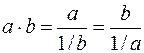, то эту неопределенность можно свести к или .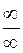

Пример 4. Для :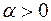

.

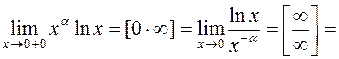
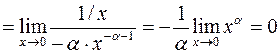Заметим, что, если иначе преобразовать произведение в частное, то применение правила Бернулли-Лопиталя приводит к усложнению неопределенности: .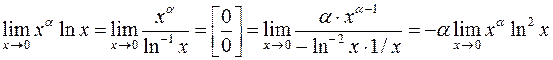

B) 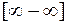. Так как 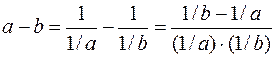,то данная неопреде-ленность сводится к виду . Часто, впрочем, того же удается достигнуть проще.

Пример 5.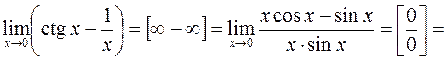

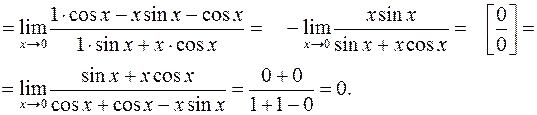
Вычисления можно упростить, если перед первым применением правила использовать эквивалентность , :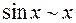

.

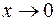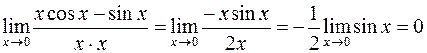С) 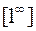, , 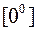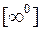. Так как 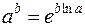(основное логарифмическое тождество) и 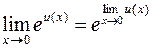(непрерывность показательной функции), то неопределенности этих типов сводятся к неопределенности вида .

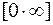Пример 6. 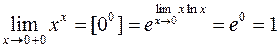(смотри пример 4).

Пример 7.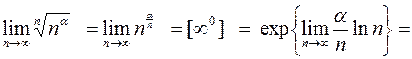

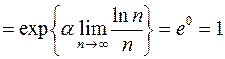(смотри пример 1).

Замечание 5. Раскрывая неопределенности по правилу Бернулли-Лопиталя, следует использовать и другие методы вычисления пределов: эквивалентности, замена переменной и т.д.

Пример 8.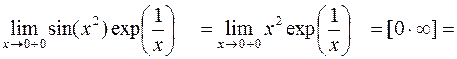

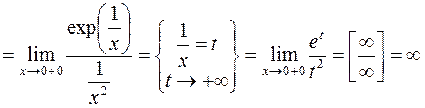(смотри пример 2).