Статистическое изучение динамики социально-экономических явлений

1. Понятие ряда динамики и виды динамических рядов

Важнейший задачей статистики является изучение изменений показателей во времени, т.е. в динамике. Эта задача решается при помощи анализа рядов динамики (временных или хронологических рядов).

Ряд динамики представляет собой ряд изменяющихся во времени значений статистического показателя, расположенных в хронологическом порядке. Составными элементами ряда динамики являются показатели уровня ряда (У) и периоды времени (годы, кварталы, месяцы, сутки) или моменты (даты) времени (t).

Уровни динамического ряда могут быть представлены абсолютными, средними или относительными величинами.

В зависимости от расстояния между уровнями ряды динамики подразделяются на:

- ряды с равноотстоящими уровнями по времени, полные – периоды следуют друг за другом или через определенные промежутки дат

- ряды с неравноотстоящимиуровнями по времени, неполные. В рядах даются прерывающиеся периоды или неравномерные промежутки между датами.

По времени, отраженному в динамических рядах, они подразделяются на:

Моментные – это ряды динамики, уровни которых характеризуют состояние явления на определенные даты (моменты времени). Например, численность населения на конец года или численность работников на 1 число какого-то месяца. Для этого ряда характерно, что в каждом последующем уровне содержится полностью или частично значение предыдущего уровня, суммировать уровни моментного ряда не следует, т.к. это приведет к повторному счету.

Интервальные(периодические) ряды - это такие ряды, уровни которых характеризуют размер явления за конкретный период времени, например, добыча нефти за 2011 г. Суммирование его значений уровней позволит получить ряды динамики более крупных периодов.

2. Показатели, характеризующие интенсивность изменения явления во времени

Анализ интенсивности изменения во времени осуществляется с помощью абсолютных и относительных показателей, получаемых в результате сравнения уровней. К таким показателям относятся: абсолютный прирост, темп роста, темп прироста, абсолютное значение одного % прироста. Если сравнению подлежат несколько последовательных уровней, то показатели ряда динамики могут вычисляться на постоянной и переменных базах сравнения. При этом принято называть сравниваемый уровень отчетным (у_i), а уровень, с которым производится сравнение, базисным (y₀).

Для расчета аналитических показателей динамики на постоянной базе каждый уровень ряда сравнивается с одним и тем же базисным уровнем. В качестве базисного выбирается либо начальный уровень ряда динамики, либо уровень, с которого начинается какой-то новый этап развития явления. Исчисленные при этом показатели называются базисными.

Для расчета аналитических показателей динамики на переменной базе каждый последующий уровень ряда сравнивается с предыдущим. Такие показатели называются цепными.

Базисные показатели ряда динамики характеризуют окончательный результат всех изменений в уровнях ряда от базисного периода до исследуемого периода. Цепные показатели ряда динамики характеризуют интенсивность изменения от периода к периоду в пределах изучаемого промежутка времени.

Абсолютный прирост (сокращение) характеризует размер увеличения (или уменьшения) уровня ряда за определенный промежуток времени. Представляет собой разность последующего и либо предшествующего, либо базисного уровня. Выражается в тех же единицах измерения, что и уровни ряда.

Δ_ц= У_i – У_i-1 Δ_б = У_i – У₀

Цепные и базисные абсолютные приросты связаны между собой: сумма последовательных цепных абсолютных приростов равна последнему базисному абсолютному приросту.

Темп (или коэффициент) роста представляет собой отношение уровня ряда к предшествующему или принятому за базу сравнения уровню и показывает, во сколько раз уровень текущего периода больше или меньше предыдущего или базисного:

Т_р^ц= 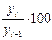Т_р^б= 100

Темп прироста (сокращения) находится как отношение абсолютного прироста либо к предыдущему уровню, либо к базисному и показывает на сколько % (или долей единицы) уровень данного периода или момента времени больше (меньше) предшествующего уровня или базисного уровня.

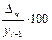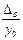Т_пр^ц= Т_пр^б= 100

или Т_пр = Т_р – 100 (или 1)

Абсолютное значение 1% прироста показывает, какое абсолютное значение скрывается за относительным показателем – 1 % прироста - и представляет отношение цепного абсолютного прироста к цепному темпу прироста, выраженному в %, за один и тот же период.

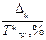|%|= или |%|=

При сравнении динамики развития двух явлений можно использовать коэффициенты опережения, представляющие собой отношение базисных или среднегодовых темпов роста за одинаковые отрезки времени по двум динамическим рядам. В числителе обычно берут наибольший темп роста, в знаменателе – наименьший. Коэффициент опережения в этом случае покажет, во сколько раз одно явление развивалось быстрее, чем другое: .

3. Обобщающие и средние характеристики ряда динамики

Для обобщающей характеристики динамики исследуемого явления определяют средние показатели: средние уровни ряда и средние показатели изменения уровней ряда.

Методы расчета среднего уровня ряда различны для интервальных и моментных рядов.

Для интервальных рядов средний уровень находится по формуле средней арифметической:

с равноотстоящими уровнями применяется средняя арифметическая простая: , где п – число уровней ряда;

а с неравноотстоящими уровнями средняя арифметическая взвешенная: 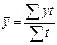, где t – длительность интервала между уровнями.

Средний уровень моментного ряда динамики определяется по средней хронологической:

с равноотстоящими уровнями применяется средняя хронологическая простая:

а с неравноотстоящими уровнями средняя хронологическая взвешенная: 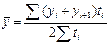, где t_i – длительность интервала между смежными уровнями.

Средний абсолютный прирост: ,

где п – число уровней ряда

Средний темп роста вычисляется двояко:

,

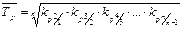где n – число цепных темпов роста

или ,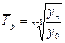

где n – число уровней ряда.

Средний темп прироста находится на основании среднего темпа роста: 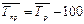(или 1).

4. Основные методы выявления тенденции изменения показателей в динамике

Выявление основной тенденции ряда является одним из методов анализа и обобщения динамических рядов. В статистике выявление основной тенденции развития производится чаще всего следующими методами: укрупнением интервалов, скользящей средней, выравниванием по среднему абсолютному приросту и аналитическим выравниванием.

Простейшим из методов выявления тенденции является укрупнение интервалов. Он основан на укрупнении периодов времени, к которым относятся уровни ряда. Средняя, исчисленная по укрупненным интервалам, например, по 3^х- летиям или 5^ти-летиям, позволяет выявлять направление и характер основной тенденции развития.

Сглаживание ряда динамики при помощи скользящей средней заключается в том, что образуется ряд теоретических уровней, в котором случайные колебания погашаются. Такие средние уровни рассчитываются по подвижным или «скользящим» периодам, например, «скользящим» 3^х- летиям или 5^ти-летиям, которые образуются путем последовательного исключения начального уровня и включения следующего за последним периодом уровня. Сглаженный ряд получается короче фактического ряда данных на 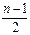уровней с каждой стороны (в начале и в конце), где п - число единиц в укрупненном периоде. При применении метода скользящей средней большое значение имеет выбор интервала скольжения. Он должен соответствовать периоду колебаний в данном динамическом ряду. (Например, цикл метеоусловий составляет 10-12 лет, поэтому для анализа урожайности в динамике период укрупнения должен равняться 10-12).

Для того, чтобы дать количественную модель, выражающую основную тенденцию изменения уровней динамического ряда во времени, используют выравнивание по среднему абсолютному приросту и аналитическое выравнивание.

Метод выравнивания по среднему абсолютному приросту применяется в случае равномерного развития явления, т.е. когда цепные абсолютные приросты близки по своим значениям. Выровненные уровни определяются: 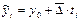, где t - порядковый номер даты, начиная с 0 для начального уровня ряда.

5. Сущность метода наименьших квадратов и применение его для проведения аналитического выравнивания

Наиболее эффективным способом выявления основной тенденции, или, иначе, тренда, является аналитическое выравнивание методом наименьших квадратов. Сущность МНК заключается в том, что подбирается уравнение, которое наиболее точно отражает характер изменения динамического ряда за изучаемый период (на практике можно использовать графическое изображение уровней ряда). Как правило, если явление развивается в арифметической прогрессии, то для выравнивания может использоваться уравнение прямой ,

где 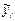- выровненное по уравнению значение уровня тренда.

– условное обозначение времени – для упрощения расчетов обычно выбирается так, чтобы :

Для нечетного ряда:	Для четного ряда:
Годы	t	Годы	t
	-2		-3
	-1		-2
			-1

При таком обозначении времени искомые параметры означают:

a₀ - средний уровень ряда динамики;

a₁ - средний абсолютный прирост (сокращение) за принятую единицу времени.

Согласно МНК, чтобы выполнялось условие минимизации суммы квадратов отклонений фактических уровней ряда от выровненных 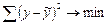, для нахождения двух неизвестных параметров надо решить систему из двух нормальных уравнений: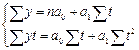

Если установлен нелинейный тип тренда, то выравнивание производят по полиному более высокого порядка, например, параболы второго порядка ,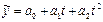

где a₀ - выровненный уровень тренда на момент или период, принятый за начало отсчета;

a₁ - средний за весь период среднегодовой прирост (сокращение), который изменяется равномерно со средним ускорением или замедлением, равным 2a₂.

a₂ - половина ускорения (замедления).

Согласно МНК для нахождения трех неизвестных параметров надо решить систему из трех нормальных уравнений:

Степень приближения выровненных значений к фактическим, т.е. целесообразность применения данной функции, оценивают по среднеквадратическому отклонению (s) и коэффициенту колеблемости . Чем они меньше, тем точнее данное уравнение отражает тенденцию ряда и именно его лучше всего использовать для прогнозирования.