Интегральная теорема Лапласа
В том случае, когда требуется найти вероятность того, что событие А появится не менее к1 и не более к2 раз в n опытах, используются интегральные формулы Лапласа:
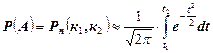(18)
или
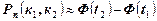, где
, 
, 
.
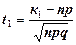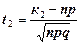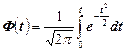Здесь функция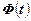 
–функция Лапласа находится по специальным таблицам 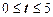при 
. При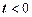 
следует иметь ввиду, что 
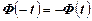. При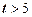 
полагают 
.
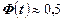Пример 18. При выпуске продукции 20% изделий не подвергаются контролю на качество. Какова вероятность того, что среди 400 изделий, выбранных случайно, окажется от 70 до 100 непроверенных изделий.
Решение. Из условия задачи вероятность того, что изделие не пройдет контроль равна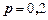 
. Тогда 
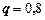. Найдем искомую вероятность по формуле 
.
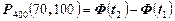Найдем
, 
.
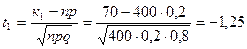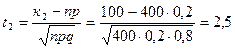Теперь по таблице находим
; 
.
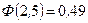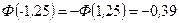Окончательно получим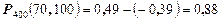 
.
Формула полной вероятности
Если событие В происходит вместе с одним из событий А1, А2,…, Аn, образующих полную группу несовместимых событий, то имеет место формула
.
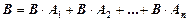Тогда вероятность события В находится по формуле полной вероятности
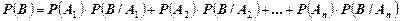(19).
Пример 19. В магазин поступили замки, изготовленные на трех заводах. Установлено, что продукция первого завода содержит 20% бракованных изделий, второго – 10%, третьего – 5%. Среди замков, взятых на реализацию, 30% изготовлено на первом заводе, 20% - на втором, 50% - на третьем. Какова вероятность купить исправный замок.
Решение. Обозначим события:
В – куплен исправный замок,
А1 – куплен замок, изготовленный на первом заводе,
А2 – куплен замок, изготовленный на втором заводе,
А3 – куплен замок, изготовленный на третьем заводе.
Тогда, так как события А1, А2, А3 несовместимые и образуют полную группу, и событие В происходит вместе с одним из этих событий, искомую вероятность найдем по формуле полной вероятности.
Представим событие В как
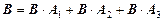
Эта формула означает, что куплен исправный замок с первого завода или со второго, или с третьего завода.
.
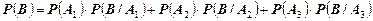Найдем все вероятности, входящие в эту формулу. Из условия задачи имеем
, 
, 
.
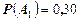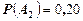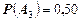Условные вероятности равны
.
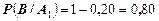
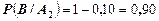
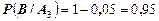Итак, получим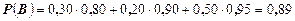 
Формула Бейеса
Эта формула применяется для нахождения условной вероятности события Аi в предположении, что событие В уже произошло. При этом известно, что событие В может произойти вместе с одним из несовместимых событий А1, А2, … Аn, образующих полную группу.
Формула Бейеса имеет вид:
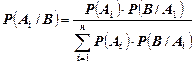(20).
Пример 20. Товар находится в трех одинаковых упаковках. В первой упаковке 20 изделий первого сорта. Во второй – 10 изделий первого сорта и 10 изделий второго сорта. В третьей – 20 изделий второго сорта. Из взятой наугад упаковки вынули изделие первого сорта. Найти вероятность того, что это изделие взято из первой упаковки.
Решение. Обозначим события:
В – взято изделие первого сорта,
А1 - взято изделие из первой упаковки,
А2 - взято изделие из второй упаковки,
А3 - взято изделие из третьей упаковки.
События А1, А2, А3 образуют полную группу. Нужно найти условную вероятность
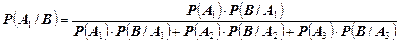
Теперь найдем вероятности всех этих событий. Так как события А1, А2, А3 равновероятны, то
.
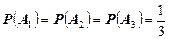Вероятность взять изделие первого сорта из первой упаковки равна
.
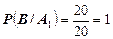Вероятность взять изделие первого сорта из второй упаковки равна
.
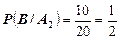Вероятность взять изделие первого сорта из третьей упаковки равна
.
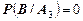Тогда, окончательно, получим
.
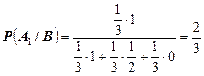Основные понятия теории массового обслуживания
Системой массового обслуживания (СМО) называется любая система, предназначенная для обслуживания каких-либо заявок (требований), поступающих в случайные моменты времени.
Примеры СМО – ремонтные фирмы, магазины, билетные кассы и т.п. Каждая СМО имеет определенное число обслуживающих единиц, которые называются каналами обслуживания. Соответственно СМО бывают одноканальные (билетная касса с одним кассиром) и многоканальные (касса с несколькими кассирами);
Кроме того СМО бывают с отказами (если все каналы заняты, заявка получает отказ и покидает СМО) и с очередью (если все каналы заняты, заявка становится в очередь и ждет, пока не освободится какой-нибудь канал).
Число мест в очереди m может быть ограниченным или неограниченным. При m = 0 СМО с очередью превращается в СМО с отказом. СМО с очередью различаются по дисциплине обслуживания: обслуживаются ли заявки в порядке поступления, в случайном порядке или некоторые заявки обслуживаются вне очереди.
СМО переходят из состояния в состояние под действием потока заявок и потока обслуживания. Заявки поступают в СМО случайно, обслуживание заявок так же продолжается случайное время. Поэтому процесс работы СМО представляет собой случайный процесс с дискретными состояниями и непрерывным временем.
Наиболее простым является Марковский процесс.
Случайный процесс называется Марковским, если для любого момента времени вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент и не зависят от того, когда и как система пришла в это состояние.
При анализе случайных процессов с дискретными состояниями пользуются геометрической схемой, которая называется графом состояний. Состояния системой изображают кружками, а переходы из состояния из состояния стрелками, соединяющими состояния.
Для математического описания Марковского процесса используется понятие потока событий.
Под потоком событий понимается последовательность однородных событий, следующих одно за другим в случайный момент времени.
Характеристикой потока служит интенсивность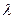 
- частота появления событий или среднее число заявок, поступающих в СМО в единицу времени.
Поток событий может быть регулярным, стационарным, потоком без последействия, ординарным.
Наиболее простыми являются простейшие потоки.
Поток событий называется простейшим, если он одновременно стационарен, ординарен и не имеет последействия.
Для них вероятность попадания на элементарный участок времени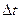 
хотя бы одного события из потока приближенно находится по формуле 
.
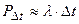О работе СМО судят по характеристикам эффективности. В качестве показателей эффективности используются:
А - абсолютная пропускная способность СМО, то есть среднее число заявок, обслуживаемое СМО в единицу времени.
Q - относительная пропускная способность, то есть вероятность обслуживания поступившей заявки.
Ротк - вероятность отказа, то есть вероятность того, что поступившая заявка не будет обслужена.
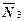- среднее число заявок, находящихся в СМО (обслуживаемых или ожидающих в очереди).
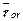- средняя длина очереди (то есть среднее число заявок в очереди).
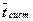- среднее время пребывания заявки в СМО (в очереди или под обслуживанием).
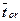- среднее время пребывания заявки в очереди.
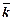- среднее число занятых каналов.
В общем случае все эти характеристики зависят от времени. Если же СМО работают в неизменных условиях достаточно долгое время, то в них устанавливается режим, близкий к стационарному. Далее не оговаривая специально, будем приводить вероятности состояний и характеристики эффективности СМО, относящиеся к предельному стационарному режиму ее работы.
СМО называется разомкнутой, если интенсивность поступающего на нее потока заявок не зависит от состояния системы. В этом случае источник заявок находится вне СМО и генерирует неограниченный поток заявок.
Для любой разомкнутой СМО справедливы формулы, связывающие ее различные характеристики эффективности:
; 
; 
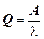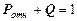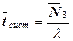; (26)
; 
.
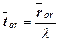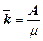Эти формулы позволяют искать не все характеристики отдельно, а лишь их часть.
Обозначим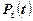 
- вероятность того, что система в момент времени t находится в состоянии Si . Эти вероятности применяются для описания случайного процесса с дискретными состояниями и находятся из системы дифференциальных уравнений.
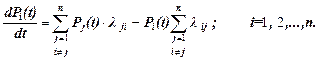(27)
Эти уравнения называются уравнениями Колмогорова. Чтобы система имела единственное решение, надо задать начальное состояние
.
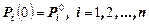Пример 24. Рассмотрим граф, приведенный на рисунке 1. У системы, описываемой этим марковским процессом, три состояния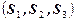 
, причем 
; 
; 
; 
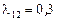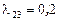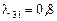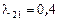
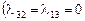и не указываются на графе).
0,8 0,2
0,4
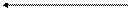
0,3
Рис. 1
Потоком вероятности перехода из состояния Si в состояние Sj называется величина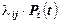 
. Уравнения Колмогорова удобно составлять по графу состояний, пользуясь правилом: производная вероятности каждого состояния равна сумме всех потоков вероятностей, идущих из других состояний в данное, минус сумма всех потоков вероятностей, идущих из данного состояния в другие. Например, для графа состояний на рис.1 получили систему уравнений
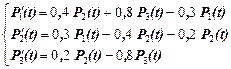
Предельный режим
Когда процесс, протекающий в системе, длится достаточно долго, возникает вопрос о значениях вероятносте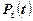й при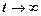 
. Если существуют предельные вероятности состояний 
, 
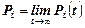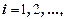то это означает, что с течением времени в системе устанавливается предельный стационарный режим, в ходе которого она переходит из одного состояния в другое, но вероятности состояний уже не меняются. В этом предельном режиме каждая предельная вероятность может быть истолкована как среднее относительное время пребывания системы в данном состоянии. Пусть число состояний конечно и равно n.
Чтобы найти предельные вероятности состояний, надо составить систему линейных алгебраических уравнений, которая получается из уравнений Колмогорова (2), если положить в них левые части (производные) равными нулю. Предельные вероятности можно найти по размеченному графу состояний, пользуясь правилом: слева в уравнениях стоит произведение предельной вероятности данного состояния на сумму интенсивностей выходящих потоков, а справа сумма произведений интенсивности входящих потоков на вероятности состояний из которых эти потоки выходят. Для решения системы к ней добавляют уравнение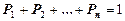 
.
Если система имеет единственное решение, то предельные вероятности состояний существуют и равны соответствующим решениям системы.
Пример 25. Найти предельные вероятности состояний системы, описываемой графом, приведенным на рис.1.
Решение.
Для этой системы по графу состояний были составлены уравнения Колмогорова (4). Положим в левых частях уравнений
.
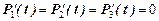Тогда получим
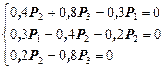
Решая эту систему совместно с уравнением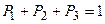 
, найдем единственное решение, которое дает предельные вероятности состояний:
; 
; 
.
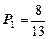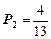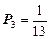Пример 26. В мастерской два мастера и одно место ожидания. Клиенты приходят через 10 минут и обслуживаются мастером 15 минут в среднем. Если место ожидания занято, клиент покидает мастерскую не обслуженным. Какую часть времени оба мастера заняты и какую свободны (потоки прихода и обслуживания клиентов считать пуассоновскими).
Решение.
Перечислим состояния системы: S0-оба мастера свободны; S1-один мастер занят, один свободен; S2-оба мастера заняты, а место ожидания свободно; S3-оба мастера и место ожидания заняты. Переход из состояния Si в состояние Si+1, i = 0, 1, 2 ..., происходит под действием потока прихода клиентов. Найдем его интенсивность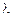 
. Так как по условию среднее время между приходами двух последовательных клиентов равно 10 минут = 
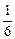ч., то получим: 
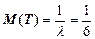; то есть 
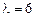. Переход из состояния S1 в состояние S0 происходит под действием потока выполнения заявок одним мастером. Его интенсивность m находится аналогично. Так как 15 минут = 
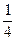ч., то 
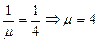. Переходы из состояния S2 в состояние S1 и из S3 в S2 происходят под действием потока, полученного объединением двух потоков выполнения заявок каждым из двух мастеров. Поэтому интенсивность его будет равна 
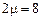. Интенсивности переходов из состояния Si в состояние Si-k, Si+k при 
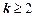, равны нулю, так как потоки ординарны, то есть события в потоках наступают «поодиночке». С учетом сказанного граф состояний будет иметь вид как на рисунке.
6 6 6
4 8 8
Найдем предельные вероятности состояний Р0, Р1, Р2, Р3. Для этого по графу состояний составим систему линейных уравнений Колмогорова.
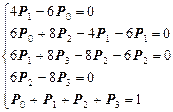
Эта система имеет единственное решение:
; 
; 
; 
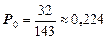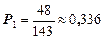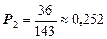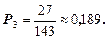
Таким образом, 22,4% времени оба мастера свободны, т.к. вероятность того, что система находится в состоянии S0 равна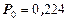 
.
Оба мастера заняты, если система находится в состоянии S2 или S3 , значит вероятность этого равна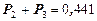 
.
Таким образом, 44,1% времени оба мастера заняты.
КОНТРОЛЬНАЯ РАБОТА №2
ВАРИАНТ 0
Найти экстремум функции F при следующих ограничениях
 |
  |
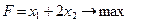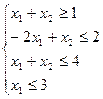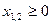2. В трех хранилищах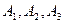 
имеется соответственно 70 т., 90 т. И 50 т. топлива. Требуется спланировать перевозку топлива четырем потребителям 
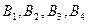, спрос которых равен соответственно 50, 70, 40 и 70 т. так, чтобы затраты на транспортировку были минимальными, если
.
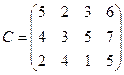3. Шесть экспертов оценивали по 10-бальной шкале модели летних шин для автомобилей, учитывая их тормозной путь, надежность управления автомобилем на прямой дороге и на поворотах, поперечные сцепные свойства, цену и др. по минимуму затрат. Результаты экспертов представлены в таблице. По данным этих оценок выбрать наиболее удачную модель (для критерия Гурвица принять к=0,6).
| Вид модели шин | эксперт | |||||
| Barum Bravuris | ||||||
| Continental PC | ||||||
| Danlop SP | ||||||
| Goodyear EV |
ВАРИАНТ 1
1. Найти экстремум функции F при следующих ограничениях
 |
 |
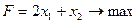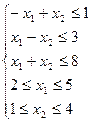2. С 3-х складов 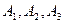необходимо доставить овощи в 5 торговых точек 
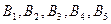. Требуется закрепить склады за торговыми точками так, чтобы общая сумма затрат на перевозку была минимальной, если 
; 
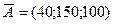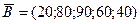
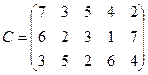
3. Торговая фирма разработала несколько вариантов плана продаж товаров на предстоящей ярмарке с учетом конъюнктуры рынка и спроса покупателей. Получающиеся от их возможных сочетаний показатели дохода представлены в таблице. Определить оптимальную стратегию фирмы в продаже товаров на ярмарке. к =0,6
| план продажи | Величина дохода, ден. ед. | ||
| Д1 | Д2 | Д3 | |
| П1 | |||
| П2 | |||
| П3 | -3 |
ВАРИАНТ 2
1. Найти экстремум функции F при следующих ограничениях
 |
 |
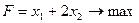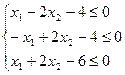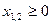2. Составить план перевозки зерна из районов 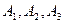и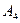 
области, в которых запасы составляют соответственно 800, 700, 1000, 500 ц на три элеватора 
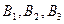мощностью соответственно 1000, 1100 и 900 ц. Затраты на перевозку 1 ц. зерна из районов на элеваторы заданы матрицей:
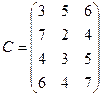
3. Шесть экспертов оценивали по 10-бальной шкале модели летних шин для автомобилей, учитывая их тормозной путь, надежность управления автомобилем на прямой дороге и на поворотах, поперечные сцепные свойства, цену и др. по минимуму затрат. Результаты экспертов представлены в таблице. По данным этих оценок выбрать наиболее удачную модель (для критерия Гурвица принять к=0,6).
| Вид модели шин | эксперт | |||||
| Barum Bravuris | ||||||
| Continental PC | ||||||
| Danlop SP | ||||||
| Goodyear EV |
ВАРИАНТ 3
1. Найти экстремум функции F при следующих ограничениях
| |
 |
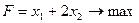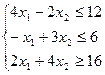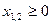2. На трех хлебокомбинатах ежедневно производится 110, 190 и 90 т муки. Эта мука потребляется 4-мя хлебозаводами, ежедневные потребности которых равны соответственно 80, 60, 160, 80 т. тарифы перевозок 1 т муки с хлебокомбинатов к каждому из хлебозаводов задается матрицей:
.
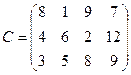Составить такой план доставки муки, при котором общая стоимость затрат на перевозки была минимальной.
3. Магазин может завести в различных пропорциях товары трех типов (А1, А2, А3); их реализация и прибыль магазина зависят от вида и состояния спроса. Предполагается, что спрос может иметь три состояния (В1, В2, В3) и не прогнозируется. Определить оптимальные пропорции в закупке товаров из условия максимизации средней гарантированной прибыли при следующей матрице прибыли: к =0,7
| Тип товара | спрос | ||
| В1 | В2 | В3 | |
| А1 | |||
| А2 | |||
| А3 |
ВАРИАНТ 4
1.Найти экстремум функции F при следующих ограничениях
 |
 |
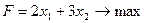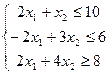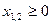2.В 3-х хранилищах горючего ежедневно хранится соответственно 175, 125 140 т бензина. Этот бензин ежедневно получают 4 АЗС в количествах, равных соответственно 180, 120, 90, 60 т. Тарифы перевозок 1 т бензина с хранилищ к АЗС задаются матрицей
.
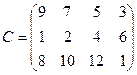Составить такой план перевозок бензина, при котором общая стоимость перевозок является минимальной.
3.Розничное торговое предприятие разработало несколько вариантов плана продажи товаров на предстоящей ярмарке с учетом меняющейся конъюнктуры рынка и спроса покупателей, получающиеся от их возможных сочетаний величины прибыли представлены в виде матрицы выигрышей. Определить оптимальный план продажи товаров. к =0,7
| Величина прибыли, тыс. руб. | ||||
| План продажи | Состояние конъюнктуры рынка и спроса | |||
| К1 | К2 | КЗ | К4 | |
| П1 | 5,0 | 4,5 | 5,1 | 4,0 |
| П2 | 4,2 | 5,6 | 3,9 | 4,3 |
| П3 | 3,6 | 4,1 | 4,7 | 4,0 |
| П4 | 3, 5 | 3,9 | 4,6 | 3,8 |
ВАРИАНТ 5
1. Найти экстремум функции F при следующих ограничениях
 |
 |
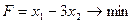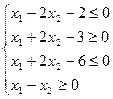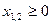2. Для строительства четырех объектов используется кирпич, изготавливаемый на 3-х заводах. Ежедневно каждый завод может изготовлять соответственно 160, 140, 60 ус. ед. кирпича. Ежедневные потребности в кирпиче на каждом из строящихся объектов соответственно равны 80, 80, 60, 80 ус. ед. кирпича. Известны также тарифы перевозок 1 ус. ед. кирпича от каждого завода к каждому строящемуся объекту:
.
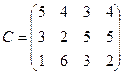Составить такой план перевозок кирпича к строящимся объектам, при котором общая стоимость перевозок является минимальной.
3.Розничное торговое предприятие разработало несколько вариантов плана продажи товаров на предстоящей ярмарке с учетом меняющейся конъюнктуры рынка и спроса покупателей, получающиеся от их возможных сочетаний величины прибыли представлены в виде матрицы выигрышей. Определить оптимальный план продажи товаров. к=0,6
| Величина прибыли, | тыс. руб. | |||
| План | Состояние конъюнктуры рынка | и спроса | ||
| продажи | К1 | К2 | КЗ | К4 |
| П1 | ||||
| П2 | ||||
| П3 | ||||
| П4 |
ВАРИАНТ 6
1. Найти экстремум функции F при следующих ограничениях
 |
 |
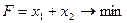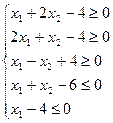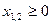2. С трех складов 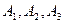необходимо доставить в четыре магазина 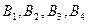сахарный песок в соответствии с заявкой каждого магазина. Составить такой план перевозки сахарного песка при котором общая стоимость затрат является минимальной, если 
; 
; 
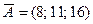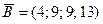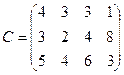
3. Экономисты оптового предприятия на основе возможных вариантов поведения поставщиков П1, П2, ПЗ, П4 разработали несколько своих хозяйственных планов О1, 02, 03, О4, а результаты всех возможных исходов представили в виде матрицы прибыли (выигрышей). Определить оптимальный план оптового торгового предприятия. k=0,8
| Хозяйственный | Прибыль по каждому варианту, тыс. руб | |||
| план | П1 | П2 | ПЗ | П4 |
| О1 | 2,3 | 3,4 | 3,0 | 3,4 |
| О2 | 3,0 | 2,9 | 2,6 | 3,7 |
| ОЗ | 2,8 | 3,8 | 3,6 | 3,0 |
| О4 | 4,0 | 2,9 | 4,0 | 4,2 |
ВАРИАНТ 7
1. Найти экстремум функции F при следующих ограничениях
 |
 |
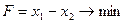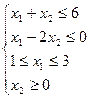2.Автотранспортная фирма обеспечивает доставку одних и тех же строительных блоков с 3-х железобетонных заводов на четыре строительные площадки. Вектор заводов поставщиков 
, вектор спроса строительных площадок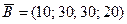 
. Тарифы на перевозку одного блока с каждого завода на соответствующую площадку заданы матрицей
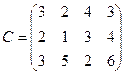
Требуется составить такой план перевозок, чтобы общая стоимость затрат на перевозки была минимальной.
3. Магазин может завести в различных пропорциях товары трех типов (А1, А2, А3); их реализация и прибыль магазина зависят от вида и состояния спроса. Предполагается, что спрос может иметь три состояния (В1, В2, В3) и не прогнозируется. Определить оптимальные пропорции в закупке товаров из условия максимизации средней гарантированной прибыли при следующей матрице прибыли: к =0,6
| Тип товара | спрос | ||
| В1 | В2 | В3 | |
| А1 | |||
| А2 | |||
| А3 |
ВАРИАНТ 8
1. Найти экстремум функции F при следующих ограничениях
 |
 |
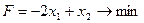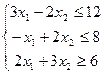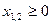2. Три шахты Кузбасса поставляют свой уголь в города А, В, С, Д, Е. По договору в А нужно поставить 60т, в В – 140т, в С – 100т, в Д – 80т, в Е – 120т. Производительность шахт соответственно равна 150т, 300т, 150т. Затраты на перевозку 1т заданы матрицей
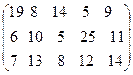
Найти такой план перевозки, чтобы удовлетворить потребности в угле данных городов и минимизировать транспортные расходы.
3. Шесть экспертов оценивали по 10-бальной шкале модели летних шин для автомобилей, учитывая их тормозной путь, надежность управления автомобилем на прямой дороге и на поворотах, поперечные сцепные свойства, цену и др. по минимуму затрат. Результаты экспертов представлены в таблице. По данным этих оценок выбрать наиболее удачную модель (для критерия Гурвица принять к=0,8).
| Вид модели шин | эксперт | |||||
| Barum Bravuris | ||||||
| Continental PC | ||||||
| Danlop SP | ||||||
| Goodyear EV |
ВАРИАНТ 9
1. Найти экстремум функции F при следующих ограничениях
 |
 |
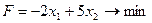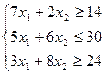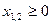2. Три кооператива поставляют овощи в четыре магазина. Кооперативы могут предложить соответственно 40, 30, 20т овощей. Магазинам требуется соответственно 30, 25, 15 и 20 т овощей. Тарифы на перевозку заданы матрицей
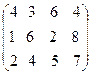
Составить план перевозки, при котором потребности магазинов удовлетворены, а транспортные расходы будут минимальны.
3. Экономисты оптового предприятия на основе возможных вариантов поведения поставщиков П1, П2, ПЗ, П4 разработали несколько своих хозяйственных планов О1, 02, 03, О4, а результаты всех возможных исходов представили в виде матрицы прибыли (выигрышей). Определить оптимальный план оптового торгового предприятия. k=0,8
| Хозяйственный | Прибыль по каждому варианту, тыс. руб | |||
| план | П1 | П2 | ПЗ | П4 |
| О1 | 1,3 | 2,4 | 2,0 | 2,4 |
| О2 | 2,0 | 1,9 | 1,6 | 2,7 |
| ОЗ | 1,8 | 2,8 | 2,6 | 2,0 |
| О4 | 3,0 | 1,9 | 3,0 | 3,2 |
МЕТОДИЧЕСКИЕ УКАЗАНИЯ